Штучні нейронні мережі є облаштуваннями паралельних обчислень, що складаються з безлічі взаємодіючих простих процесорів. Такі процесори зазвичай виключно прості, особливо порівняно з процесорами, використовуваними в персональних комп'ютерах.
Кожен процесор подібної мережі має справу тільки з сигналами, які він періодично отримує, і сигналами, які він періодично посилає іншим процесорам, і, проте, будучи сполученими в досить велику мережу з керованою взаємодією, такі локально прості процесори разом здатні виконувати досить складні завдання.
Нейронна мережа є сукупністю елементів, сполучених деяким чином так, щоб між ними забезпечувалося взаємодія. Ці елементи, що називаються також нейронами або вузлами, являють собою прості процесори, обчислювальні можливості яких зазвичай обмежуються деяким правилом "комбінування вхідних" сигналів і правилом активізації, що дозволяє вичислити вихідний сигнал по сукупності вхідних сигналів.
Вихідний сигнал елементу може посилатися іншим елементам по зважених зв'язках, з кожною з яких пов'язаний ваговий коефіцієнт або вага. Залежно від значення вагового коефіцієнта передаваний сигнал або посилюється, або послаблюється. Елемент нейронної мережі схематично показаний на мал. 5.3.
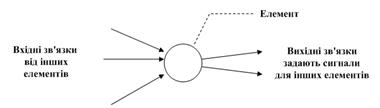
Мал. 5.3 Окремий элемент мережі
Один з найпривабливіших аспектів використання нейронних мереж полягає в тому,що, хоча елементи такої мережі мають дуже обмежені обчислювальні можливості, уся мережа в цілому, об'єднуючи велике число таких елементів, виявляється здатною виконувати складні завдання.
Структура зв'язків відбиває деталі конструкції мережі, а саме те, які елементи сполучені, в якому напрямі працюють з'єднання і який рівень значущості(тобто вага) кожного із з'єднань. Завдання, яке розуміє мережу (чи її програма), описується в термінах вагових значень зв'язків, що зв'язують елементи.
Структура зв'язків зазвичай визначається в два етапи: спочатку розробник системи вказує які елементи мають бути пов'язанні і в якому напрямі, а потім в процесі фази навчання визначаються значення відповідних вагових коефіцієнтів.
Вагові коефіцієнти можна визначити і без проведення навчання, але якраз найбільша перевага нейронних мереж полягає в їх здатності навчатися виконанню завдання на основі тих даних, які мережа отримуватиме в процесі реальної роботи.
Для багатьох застосувань навчання є не лише засобом програмування мережі, коли немає достатніх знань про спосіб рішення задачі, що дозволяють виконати програмування в традиційній формі, але єдиною метою навчання є перевірка того, що мережа дійсно зможе навчитися вирішувати поставлені перед нею завдання.
- Безліч простих процесорів
- Структура зв'язків
- Правило поширення сигналів в мережі
- Правило комбінування сигналів, що входять
- Правило обчислення сигналу активності
- Правило навчання, що коригує зв'язки
Безліч простих процесорів
З кожним процессором (тобто оброблювальним елементом мережі) пов’язується набір вхідних зв’язків, по яких до цього елементу поступають сигнали від інших елементів мережі, і набір вихідних зв'язків, по яких сигнали цього елементу передаються іншим елементам. Деякі елементи призначені для отримання сигналів із зовнішнього середовища (і тому називаються вхідними елементами), а деякі - для виведення в зовнішнє середовище результатів обчислень (і тому такі елементи мережі називаються вихідними елементами).
Будь-яка обчислювальна машина має хоч би один пристрій введення (наприклад, клавіатуру), за допомогою якого система отримує дані із зовнішнього середовища, і пристрій виведення (наприклад, монітор), за допомогою якого відображаються результати обчислень. У випадку програмного моделювання реальних процесів на вхідні елементи зазвичай подаються вже заздалегідь підготовлені дані з деякого файлу даних, а не від безпосередньо пов'язаних із зовнішнім середовищем датчиків.
Структура зв'язків відображає те, як сполучені елементи мережі. У одній моделі (тобто для одного типу мереж) кожен елемент може бути пов'язаний з усіма іншими елементами мережі, в іншій моделі елементи можуть бути організовані в деякій впорядкованій по рівнях (шарам) ієрархії, де зв'язки допускаються тільки між елементами в суміжних шарах, а в третій - можуть допускатися зворотні зв'язки між суміжними шарами або усередині одного шару, або ж допускатися посилка сигналів елементами самим собі.
Можливості тут практично нескінченні, але зазвичай для кожної конкретної моделі мережі вказується тип допустимих зв'язків. Кожен зв'язок визначається трьома параметрами: елементом, від якого виходить цей зв'язок, елементом, до якого цей зв'язок спрямований, і числом (зазвичай дійсним), що вказує ваговий коефіцієнт (тобто вага зв'язку). Негативне значення ваги відповідає пригніченню активності відповідного елементу, а позитивне значення - посиленню його активності.
Абсолютне значення вагового коефіцієнта характеризує силу зв'язку.
Структура зв'язків зазвичай представляється у вигляді вагової матриці W, в якій кожен елемент wij представляє величину вагового коефіцієнта для зв'язку, що йде від елементу i до елементу j (зверніть увагу на те, що у багатьох публікаціях зв'язку у вагових матрицях вважається, що йдуть від елементу j до елементу i, що, очевидно, слідує враховувати при представленні матричних і векторних операцій). Для опису структури зв'язків може використовуватись не одна, а декілька вагових матриць, якщо елементи мережі виявляються згрупованими в шари.
Правило обчислення сигналу активності
Для усіх елементів є правило обчислення вихідного значення, яке передбачається передати іншим елементам або в зовнішнє середовище (якщо йдеться про вихідний елемент, що представляє кінцевий результат обчислень). Це правило називають функцією активності, а відповідне вихідне значення називають активністю відповідного елементу.
Активність може представлятися або деяким дійсним значенням довільного виду, або дійсним значенням з деякого обмеженого інтервалу значень (наприклад, з інтервалу [0, 1], або ж деяким значенням з певного дискретного набору значень (наприклад {0, 1} чи {1, - 1})). На вхід функції активності поступає значення комбінованого введення цього елементу. Приклади функцій активності наводяться нижче.
Тотожна функція
Функція активності для вхідних елементів може бути тотожною функцією, і це просто означає, що значення активності (сигнал, що посилається іншим елементам) опиняється в точності рівним комбінованому введенню(мал. 5.4). Вхідні елементи зазвичай призначені для розподілу сигналів, що вводяться між іншими елементами мережі, тому для вхідних елементів зазвичай вимагається, щоб витікаючий від елементу сигнал був таким же, як і що входить. На відміну від інших елементів мережі, вхідні елементи мають тільки по одному вхідному значенню.
Наприклад, кожен вхідний елемент може отримувати сигнал від одного датчика, що відповідає йому, розміщеного на фюзеляжі літака. Один цей елемент зв'язується з багатьма іншими елементами мережі, так що дані, отримані від одного датчика, виявляються розподіленими між багатьма елементами мережі. Оскільки вхідні елементи призначені виключно для того, щоб розподіляти сигнали, що отримуються із зовнішнього середовища, багато дослідників взагалі не вважають вхідні елементи частиною нейронної мережі.

f(net)=net
Мал. 5.4. Тут активність в точності дорівнює комбінованому введенню. Зверніть увагу на те, що активність позначається символом f(net)
Порогова функція
У більшості моделей нейронних мереж використовуються нелінійні функції активності. Порогова функція обмежує активність значеннями 1 або 0 залежно від значення комбінованого введення порівняно з деякою пороговою величиною в (мал. 5.5).

Мал. 5.5. Порогова функція
Найчастіше зручніше відняти порогове значення (що називається зміщенням або зрушенням) зі значення комбінованого введення і розглянути порогову функцію в її математично еквівалентній формі, показаній на мал. 5.6.. Зрушення w0 в даному випадку виявляється негативним, а значення комбінованого введення обчислюється за формулою.

Мал. 5.6. Порогова функція із врахованим зрушенням
Зрушення зазвичай інтерпретується як зв'язок, витікаючий від елементу, активність якого завжди дорівнює 1(мал. 5.7). Комбіноване введення в даному випадку можна представити у виді: 

Мал. 5.7. Для зручності компонент зміщення часто интерпретується як зв'язок з елементом попереднього шару в припущенні, що активність цього елементу завжди дорівнює 1
Сигмоїдальна функція
Найчастіше використовуваною функцією активності є сигмоїдальна функція. Вихідні значення такої функції безперервно заповнюють діапазон від 0 до 1. Прикладом може служити логістична функція, показана на рис. 5.8:


Мал. 5.8 Сигмоїдальна функція






