Стратегії евристичного пошуку є ефективнішими з точки зору споживаних ресурсів пам'яті і процесорного часу, ніж стратегії сліпого пошуку. Стратегії евристичного пошуку здійснюють вибір вузла, що піддається розширенню, на підставі додаткових знань про проблему, що дозволяють на кожному кроці монотонно наближатися до рішення.
У просторі станів пошуку евристика визначається як набір правил для вибору тих гілок з простору станів, які з найбільшою вірогідністю приведуть до прийнятного рішення проблеми.
Поведінку евристики можна оцінювати по ряду параметрів. Наприклад, разом з рішенням задачі може знадобитися алгоритм знаходження найкоротшого шляху до нього. Це важливо, коли кожен додатковий крок до мети має дуже високу вартість, наприклад, при плануванні шляху для автономного робота в небезпечному середовищі. Евристика, яка знаходить найкоротший шлях до мети, називається допустимою(admissible). У інших застосуваннях найкоротший шлях до рішення може бути не так важливий, як загальна ефективність рішення задачі.
Одна з найбільш простих стратегій евристичного пошуку базується на мінімізації оцінки вартості рішення з кожного кроку пошуку. Ця стратегія часто називається стратегія "жадібного" пошуку (greedy search). Функція, за допомогою якої здійснюється обчислення оцінки вартості рішення з кожного кроку, називається евристичною функцією(heuristic function). Евристичну функцію визначимо таким чином
h(n) =<оцінка вартості найбільш дешевого шляху з вузла n до цільового вузла>
Стратегія "жадібного" пошуку використовує функцію h для вибору чергового розширюваного вузла. Функція h може мати будь-який вигляд і зазвичай набуває нульового значення досягши цільового вузла. Проілюструємо стратегію "жадібного" пошуку на прикладі рішення задачі знаходження шляху з міста A в місто Z. В якості евристичної функції виберемо функцію, задаючу найкоротшу відстань, "по прямій", з поточного міста до міста Z.
hКР(n) = <найкоротша відстань з міста n до міста Z>
Стратегія відшукує рішення не розширюючи вузли, які не знаходяться на шляху до цільового вузла. "Жадність" стратегії проявляєтся в тому, що вона вибирає вузол, використовуючи оцінки тільки в межах поточного кроку і не оцінюючи увесь шлях. Наслідком цього є не оптимальність стратегії, що полягає в тому, що вона не гарантує знаходження найкращого шляху. Другим слідством, витікаючим із стратегії "жадібного" пошуку є можливість попадання у безвихідь, або у вузол, який не має спадкоємців.
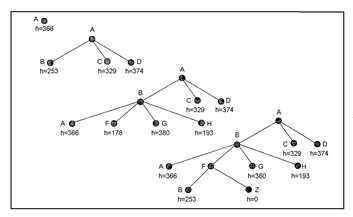
Мал. 5.1 ілюструє розвиток "жадібного" пошуку при вирішенні задачі знаходження шляху з міста A в місто Z.
До недоліку стратегії "жадібного" пошуку відноситься також його незавершеність. Стратегія може нескінченно поглиблювати дерево пошуку і ніколи не повернеться, щоб перевірити інші можливі шляхи.
Стратегія А* пошуку позбавлена відмічених недоліків стратегії "жадібного" пошуку і має властивості оптимальності і завершеності. Ця стратегія, для вибору чергового розширюваного вузла, використовує функцію загальної вартості шляху, сумою функції вартості усього шляху, що являється, - g(n) і евристичній функції оцінки рішення з поточного кроку - h(n):
f(n) = g(n) h(n)
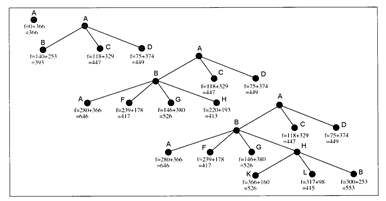
Мал. 5.2 ілюструє розвиток пошуку по алгоритму А* при рішенні задачі знаходження шляху з міста A в місто Z.
Стратегія пошуку А*вибирає для розширення вузол що має найменше значення функції f(n). На евристичну функцію h(n) зазвичай накладається обмеження, що полягає в тому, що функція h(n) не повинна переоцінювати(overestimates) вартість рішення. Евристична функція, що має таку властивість, називається - допустимою евристикою. Якщо h(n) допустима евристика, то f(n) ніколи не переоцінить реальну вартість кращого рішення з n, що забезпечує стратегії А* пошуку властивості оптимальності і завершеності. На мал. 5.2 приведені декілька перших кроків стратегії А* пошуку шляху з міста А в місто Z. В якості допустимої евристики вибрана функція hКР(n).






