 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
 .
.
Вариант 24
Задача 1. Вычислить предел числовой последовательности.
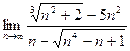 .
.
Задача 2. Вычислить предел функции.
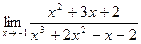 .
.
Задача 3. Найти производную функции.
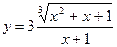 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
 .
.
Вариант 25
Задача 1. Вычислить предел числовой последовательности.
 .
.
Задача 2. Вычислить предел функции.
 .
.
Задача 3. Найти производную функции.
 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
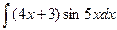 .
.
Вариант 26
Задача 1. Вычислить предел числовой последовательности.
 .
.
Задача 2. Вычислить предел функции.
 .
.
Задача 3. Найти производную функции.
 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
 .
.
Вариант 27
Задача 1. Вычислить предел числовой последовательности.
 .
.
Задача 2. Вычислить предел функции.
 .
.
Задача 3. Найти производную функции.
 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
 .
.
Вариант 28
Задача 1. Вычислить предел числовой последовательности.
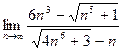 .
.
Задача 2. Вычислить предел функции.
 .
.
Задача 3. Найти производную функции.
 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
 .
.
Вариант 29
Задача 1. Вычислить предел числовой последовательности.
 .
.
Задача 2. Вычислить предел функции.
 .
.
Задача 3. Найти производную функции.
 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
 .
.
Вариант 30
Задача 1. Вычислить предел числовой последовательности.
 .
.
Задача 2. Вычислить предел функции.
 .
.
Задача 3. Найти производную функции.
 .
.
Задача 4. Исследовать и построить график функции.
 .
.
Задача 5. Найти неопределенный интеграл.
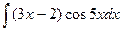 .
.
Вариант 31
Задача 1. Вычислить предел числовой последовательности.
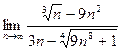 .
.
Задача 2. Вычислить предел функции.
 .
.
Задача 3. Найти производную функции.
 .
.
Задача 4. Исследовать и построить график функции.
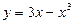 .
.
Задача 5. Найти неопределенный интеграл.
 .
.
Вопросы для самоконтроля
1. Понятие множества, операции над множествами.
2. Числовая ось. Модуль числа. Окрестность точки.
3. Постоянные и переменные величины.
4. Функция и способы ее задания. Свойства функций: четность и нечетность, ограниченность, периодичность, монотонность.
5. Обратная функция. Сложная функция. Основные элементарные функции.
6. Элементарные функции и их классификация.
7. Преобразование графиков функций.
8. Интерполирование функций
9. Числовые последовательности и их пределы.
10. Предел функции в конечной точке и на бесконечности. Свойства пределов. Односторонние пределы. Первый и второй замечательные пределы. Способы вычисления пределов.
11. Непрерывность функции в точке и на отрезке. Определение точек разрыва, их классификация.
12. Производная функции одной переменной, таблица производных, вычисление производных.
13. Дифференциал функции одной переменной, эластичность функции.
14. Производные и дифференциалы высших порядков.
15. Основные теоремы дифференциального исчисления.
16. Правило Лопиталя. Формулы Тейлора.
17. Исследование функций и построение графиков.
18. Первообразная функции. Неопределенный интеграл, его свойства. Таблица основных неопределенных интегралов.
19. Методы интегрирования: метод подстановки, интегрирование по частям, интегрирование рациональных и некоторых иррациональных функций.
20. Определённый интеграл как предел интегральных сумм при вычислении площади криволинейной трапеции. Формула Ньютона-Лейбница.
21. Замена переменных и метод интегрирования по частям определённого интеграла. Определенный интеграл с переменным верхним пределом.
22. Несобственный интеграл.
23. Геометрическое и экономическое приложения определённого интеграла.
24. Дифференциальные уравнения (ДУ) первого порядка.
25. Некоторые виды ДУ 1-го порядка.
26. Линейные ДУ 1-го порядка.
27. Линейные ДУ с постоянными коэффициентами.
28. ДУ в экономике.
29. Числовые ряды.
30. Степенные ряды.
31. Основные понятия функции нескольких переменных.
32. Предел и непрерывность, частные производные, дифференциал функции нескольких переменных.
33. Производная по направлению, градиент, экстремумы, выпуклость функции нескольких переменных.
34. Применение функций нескольких переменных в экономике, метод наименьших квадратов.






