МОДУЛЬ II. ПРАКТИКУМ
ПО ДИСЦИПЛИНЕ
Математика
(Наименование дисциплины (модуля))
Направление подготовки
09.03.01 Информатика и вычислительная техника
13.03.01 Теплоэнергетика и теплотехника
13.03.02 Электроэнергетика и электротехника
Профиль подготовки
«Автоматизированные системы обработки и управления»
«Автоматизация технологических процессов и производств в теплоэнергетике и теплотехнике»
«Менеджмент в электроэнергетике и электротехнике»
Квалификация (степень) выпускника
Бакалавр
Форма обучения
очная, заочная
СОДЕРЖАНИЕ
1. Планы практических занятий с примерами решения задач по темам:
1) «Пределы»
2) «Производная»
3) «Исследование функций»
4) «Неопределенный интеграл»
5) «Определенный интеграл и его приложения»
6) «Дифференциальные уравнения»
7) «Ряды»
2. Варианты контрольной работы ……………………………СТР.65-80
3. Вопросы для самоконтроля …………………………………. стр. 80
Планы практических занятий
Практические занятия проводятся для углубленного изучения слушателями всех разделов дисциплины, овладения практическими навыками решения задач. На них отрабатываются ключевые моменты предмета, закрепляются знания, полученные во время лекций и самостоятельной работы.
Практическое(ие) занятие(я) по теме
«Пределы»
Цель: Углубленное усвоение лекционного занятия и проверка знаний студентов по теме, научиться решать задачи по теме.
Планы занятий:
Решение задач и одновременное повторение основных терминологий и алгоритмов. Примеры решения задач:
Пример 1. Вычислить пределы
Решение
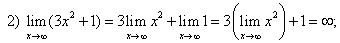
Пример 2. Вычислить пределы
Решение
Пример 3 Вычислить пределы:
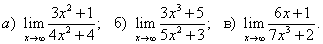
Решение
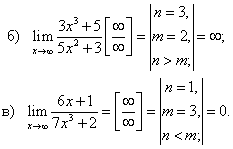
Пример 5. Вычислить пределы
Решение
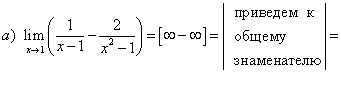
Пример 6.
х = 3 ¾ точка устранимого разрыва.
Функцию можно доопределить до непрерывной функции:
y = x +3¾ непрерывная функция.
Пример 7.
y = [ x ] ¾ целая часть числа.
Рассмотрим точку х = 1.
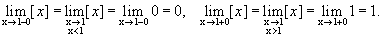
Следовательно, х = 1 ¾ точка разрыва первого рода, скачок в ней равен единице.
Пример 8. Рассмотрим функцию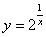 
в точке х = 0.
Следовательно, х = 0 ¾ точка разрыва второго рода.
Пример 9. Вычислить пределы
Решение
Пример 10. Вычислить пределы:
Решение
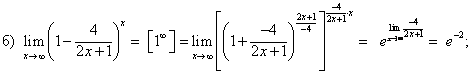
Пример 11. Найти предел
Решение
Обозначим
. Тогда условие x → 0, y → 0 равносильно тому, что r → 0 и искомый предел примет вид:
Основная литература
1. Шипачёв, В.С. Высшая математика: учебник для вузов.- 8-е изд., стер.- М.: Высшая школа, 2007.- 479с., илл. ББК 22.1 МО
2. Башмаков, М.И. Математика. Сборник задач профильной направленности: учеб. пособие для СПО.- М.: Академия, 2012.- 208с. ББК 22.1 ФИРО
3. Башмаков, М.И. Математика. Задачник: учеб. пособие для СПО.- М.: Академия, 2012.- 416с. ББК 22.1 ФИРО
4. Федорова Н.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7227-3
5. Лукша В.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7228-0
6. Гунько Ю.А. Математический анализ. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7230-3
7. Щербакова Ю.В. Дифференциальные уравнения. Учебное пособие. Научная книга. 2012.
8. Боронина Е.Б. Математический анализ. Учебное пособие. Научная книга. 2012.
Дополнительная литература
1. Высшая математика для экономистов: Учебник / Кремер Н.Ш. - М.: Юнити, 2006, 2008, 2009.
2. Сборник задач по высшей математике для экономистов: Учб. пособ./ Под ред. В.И. Ермакова-М.:ИНФРА-М,2004.
3. Общий курс высшей математики (для экономистов): Учебник / Под ред. Ермакова В.И. – М.: Инфра-М, 2003.
4. Кузнецов Б. Т. Математика. М., ЮНИТИ, 2004
Формы текущего контроля знаний: решение задач.
Формы контроля самостоятельной работы студентов: ответы на вопросы, проверка решения задач, заданных на дом.
