«Производная»
Цель: Углубленное усвоение лекционного занятия и проверка знаний студентов по теме, научится решать задачи по теме.
Планы занятий:
Решение задач и одновременное повторение основных терминологий и алгоритмов. Примеры решения задач:
Пример 1. у = |х|, х 0=0.


Пример 2. Найти производные функции:
а) y = 2 x 5 – 5 × 2 x + 4 x – 7log2 x – ln 2;
б) y = (1 + x 2) × arctg x;

Решение:
а) Используя правила дифференцирования, получим:
y' = (2 x 5) ' – (5 × 2 x) ' + (4 x) ' – (7log2 x) ' – (ln 2) ' =
= 2 × (x 5) ' – 5 × (2 x) ' + 4 (x) ' – 7 × (log2 x) ' – 0 =

б) Используя правила дифференцирования, получим:
y' = (1 + x 2) ' × arctg x + (1 + x 2) ' × (arctg x) ' =

в) Используя правила дифференцирования, получим:


В точке х 0=0функция непрерывна, но производной не существует.
Пример 3. Вычислить дифференциал для y = x 2.
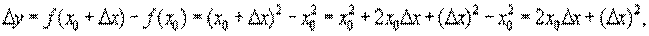

Пример 4. Найти среднюю скорость движения тела, совершаемого по закону S = 6 t 2 + 1, для промежутка времени от t 1 = 1 до t 2 = 3.
План решения
1. Найти мгновенную скорость v (t) = S' (t) в момент времени t, воспользовавшись формулами:
1. (u ± v) ' = u' ± v';
2. (Cu) ' = Cu', C = const;
3. C' = 0.
3. (xn) ' = nxn – 1.
2. Найти значение скорости в момент времени t 1 и t 2, т.е. v (t 1) и v (t 2).
3. Найти среднее значение скорости.
Решение
v (t) = S' (t) = (6 t 2 + 1) ' = (6 t 2) ' + 1 ' = 12 t.
v (t 1) = v (1) = 12 · 1 = 12.
v (t 2) = v (3) = 12 · 3 = 36.
vср. = 23.
Пример 5. Найти производные функций:




Решение:

б) По правилу дифференцирования произведения двух функций <…>

в) По правилу дифференцирования частного двух функций <…>

Учитывая, что (sin2 х)' = 2sin x (sin x)' = 2sin x cos x = sin 2 x,

после преобразований получаем

г) Применяя метод логарифмического дифференцирования, находим вначале

Теперь

Пример 6. Найти производные функций у'х:
а) еy + е - х + ху = 0;
Решение, а) При дифференцировании неявно заданной функции учитываем, что у есть функция от х, получаем
ey × y ¢ + e - x (- x)¢ + x ¢ y + xy ¢ = 0 или
ey × y ¢ - e - x + y + xy ¢ = 0, откуда



Используя правило дифференцирования функций, заданных параметрически, получаем

Отсюда

Пример 7. Пользуясь правилом Лопиталя, вычислить следующие пределы:

Решение




прологарифмируем обе части этого равенства.


ln y = 0 Þ y = e 0 = 1. Таким образом,

Пример 8. Вычислить частные производные для 
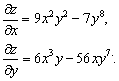
Пример 9. Вычислить частные производные для 

Пример10. Вычислить полный дифференциал


Пример 11. Вычислить частные производные для 


Пример 12. Найти частные производные второго порядка функции двух переменных
z = ln(1 +x + 2у).
Решение
Частные производные 1-го порядка имеют вид:

Считая их новыми функциями двух переменных, найдем их частные производные. Получаем:


Основная литература
Основная литература
1. Шипачёв, В.С. Высшая математика: учебник для вузов.- 8-е изд., стер.- М.: Высшая школа, 2007.- 479с., илл. ББК 22.1 МО
2. Башмаков, М.И. Математика. Сборник задач профильной направленности: учеб. пособие для СПО.- М.: Академия, 2012.- 208с. ББК 22.1 ФИРО
3. Башмаков, М.И. Математика. Задачник: учеб. пособие для СПО.- М.: Академия, 2012.- 416с. ББК 22.1 ФИРО
4. Федорова Н.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7227-3
5. Лукша В.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7228-0
6. Гунько Ю.А. Математический анализ. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7230-3
7. Щербакова Ю.В. Дифференциальные уравнения. Учебное пособие. Научная книга. 2012.
8. Боронина Е.Б. Математический анализ. Учебное пособие. Научная книга. 2012.
Дополнительная литература
1. Высшая математика для экономистов: Учебник / Кремер Н.Ш. - М.: Юнити, 2006, 2008, 2009.
2. Сборник задач по высшей математике для экономистов: Учб. пособ./ Под ред. В.И. Ермакова-М.:ИНФРА-М,2004.
3. Общий курс высшей математики (для экономистов): Учебник / Под ред. Ермакова В.И. – М.: Инфра-М, 2003.
4. Кузнецов Б. Т. Математика. М., ЮНИТИ, 2004
Формы текущего контроля знаний: решение задач.
Формы контроля самостоятельной работы студентов: ответы на вопросы, проверка решения задач, заданных на дом.






