Рассмотрим квадратную матрицу 2-го порядка:
Определение. Определителем 2-го порядка, соответствующим матрице А, называется число
.
Числа а11, а12, а21, а22 называются элементами определителя (они же элементы матрицы А).
Элементы а 11, а 22 составляют главную диагональ, а элементы а 21, а 12 – побочную диагональ.
Пусть дана квадратная матрица 3-го порядка:
.
Определение. Определителем 3-го порядка, соответствующим матрице А, называется число D, которое определяется выражением:
Элементы а 11, а 22, а 33 – расположены на главной диагонали, элементы а 13, а 22, а 31 – на побочной диагонали.
Вычисление определителей 2-го и 3-го порядка
Определитель 2-го порядка вычисляется по определению:
.
Пример 1
Для вычисления определителя 3-го порядка можно воспользоваться следующими правилами:
Правило Саррюса: дописать справа к элементам определителя сначала 1-й столбец, затем 2-й (можно внизу дописать первую и вторую строки), (рис.1), произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «плюс», а произведение элементов побочной диагонали и двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «минус» (рис. 1). Сумма этих шести произведений дает определитель 3-го порядка, соответствующий матрице А.
,
- - - + + +
Рис. 1
Пример 2
Вычислить 
.
Решение
,
– – – + + +
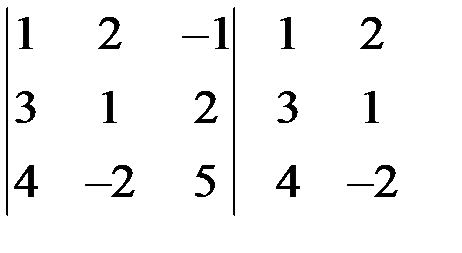таким образом:
Правило треугольника: одно из трех слагаемых, со знаком «плюс» есть произведение элементов главной диагонали определителя, каждое из двух других – произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла определителя, слагаемые со знаком «минус» строятся так же, но относительно побочной диагонали (рис.2).
(+) (-)
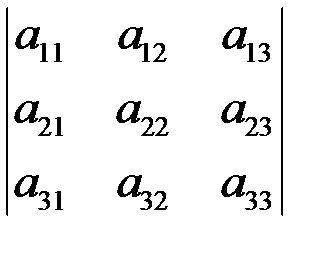
Рис. 2
Пример 3
Вычислить определитель по правилу треугольника: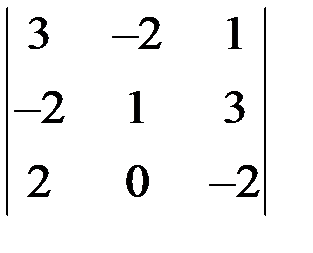 
.
Решение
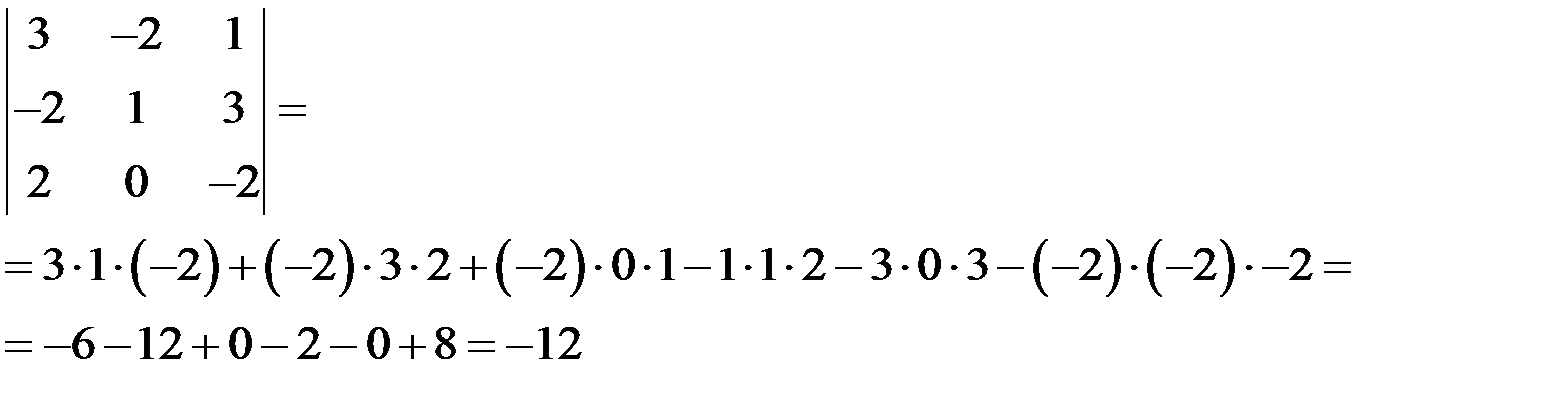
Свойства определителей
Рассмотрим свойства определителей на примере определителя 3-го порядка.
Рассмотрим определитель:
.
Определение. Минором некоторого элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, на пресечении которых стоит этот элемент. Обозначение минора 
.
Пример 4
Минор элемента а12: 
.
Определение. Алгебраическим дополнением любого элемента определителя называется минор этого элемента, взятый со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит этот элемент, есть число четное, либо с противоположным знаком, если эта сумма есть число нечетное. Обозначение алгебраического дополнения Аij.
Пример 5
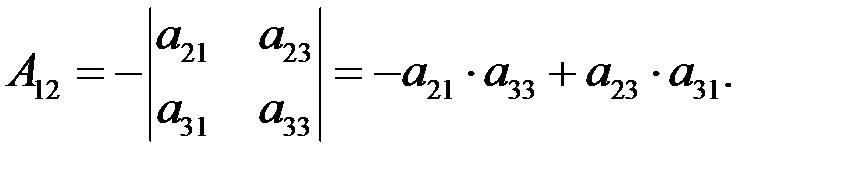
Свойство 1. Определитель равен сумме произведений элементов какого-нибудь столбца (или строки) на их алгебраические дополнения.
Пример 6
Вычислим определитель, разложив его по элементам 1-ой строки:
.
Свойство 2. Величина определителя не изменится, если каждую его строку заменить столбцом с тем же номером.
Свойство 3. Перестановка двух столбцов или двух строк определителя равносильна его умножению на (–1).
Свойство 4. Общий множитель всех элементов одного столбца или одной строки определителя можно вынести за знак определителя.
Свойство 5. Если все элементы какой-либо строки или какого-либо столбца равны нулю, то определитель равен нулю.
Свойство 6. Определитель, имеющий два одинаковых столбца или две одинаковых строки, равен нулю.
Свойство 7. Определитель равен нулю, если элементы двух столбцов или двух строк пропорциональны.
Свойство 8. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые слагаемые, а во втором – вторые:
.
Свойство 9. Если к элементам некоторого столбца (или строки) определителя прибавить соответствующие элементы другого столбца (или строки), умноженные на общий множитель, то величина определителя не изменится.
Пример 7
Вычислим определитель:
,
при вычислении определителя первую строку умножили на 2 и сложили со второй, затем разложили определитель по 2-й строке.
Свойство 10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или строки) определителя равна нулю.
Обратная матрица
Пусть дана квадратная матрица А порядка n.
Обратной матрицей по отношению к данной А называется матрица 
, которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
По определению
А · 
= · А = Е.
Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной.
Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
,
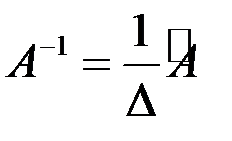где 
- определитель матрицы А, 
- союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
,
для квадратной матрицы 3-го порядка союзной является матрица
.
Пример
Для матрицы 
найти обратную.
Решение
Обратную матрицу находим по формуле
.
Определитель матрицы 
, следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
.
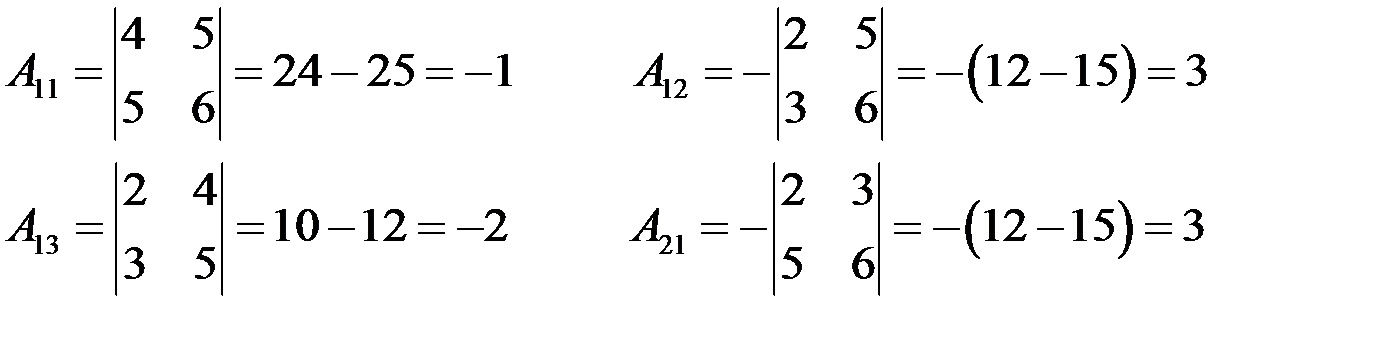
Тогда обратная матрица имеет вид
.
