Из таблицы для функции двух переменных видно, что элементарные функции типа отрицания, дизъюнкции, конъюнкции, Шеффера, Пирса и т.д. находятся в связи друг с другом. Посмотрим эти связи и свойство этих исходных функций.
Конъюнкция, дизъюнкция, отрицание (и, или, не). Используя основные положения алгебры логики можно убедиться в справедливости следующих аксиом
1) 
, что означает возможность исключения из логического выражения всех членов имеющих двойное отрицание, заменив их исходной величиной.
2) x+x=x; x*x=x эти преобразования позволяют сократить длину логических выражений.
3) х+0=х
4) х+1=1
5) х*0=0
6) х*1=х
7) 
8)
Дизъюнкция и конъюнкция обладают рядом свойств, аналогично свойствам обычных арифметических операций сложения и умножения. А именно:
1) Свойства ассоциативности или сочетательный закон:
2) Свойства коммутативности, переместительный закон:
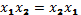
3) Свойства дистрибьютивности или распределительный закон:
а) Для конъюнкции относительно дизъюнкции:
б)Для дизъюнкции относительно конъюнкции:
Это свойство фактически определяет правило раскрытия скобок или взятия в скобки логических выражений.
Законы Де-Моргана.
Несложно установить правильность следующих соотношений:
Из этого закона вытекает, что 
и 
. С помощью этих соотношений появляется возможность выражать конъюнкцию через дизъюнкцию и отрицание или наоборот.
Законы Де-Моргана справедливы для любого числа переменных, т.е.
Для логической функции устанавливается соотношения известные как законы поглащения:
1) 
2) 
| х1 | х2 | х1+х2 | х1х2 | х1+(х1х2) | х1(х1+х2) |
Сложение по модулю два.
Эта функция выражается следующим образом:
Функция сложения по модулю два обладает свойствами:
1) Свойство коммутативности, переместительный закон:
2) Свойства ассоциативности:
3) Свойства дистрибьютивности или распределительный закон:
Для этой функции справедливы следующие аксиомы:
На основании аксиом и свойств можно вывести правила перевода функций «и», «или»,
«не» через функцию сложения по модулю два и наоборот:
Функция импликации.
Это функция выражается следующим образом:
Для функции импликации справедливы аксиомы:
Из этих аксиом следует, что импликация обладает только свойствами коммутативности, но в несколько измененном виде:
Функции «и», «или», «не» через импликацию выражаются:
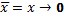
Функция Шеффера.
Это функция, которая может быть выражена:
Для нее характерны аксиомы:
Для функции Шеффера справедливо только свойство коммутативности, т.е.:
Из этих аксиом и свойств можно получить формулу преобразования функции «и», «не», «или» через функцию Шеффера:
Функция Пирса-Вебба.
Это функция описывается следующем выражением:
Для этой функции справедливы аксиомы:
Эта функция обладает только свойством коммутативности:
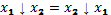
Функция «и», «или», «не» через функцию Пирса-Вебба выражается следующим образом:
