Это первое отличие чисел с ПЗ

Второе отличие – плотность. Она неравномерна. Числа с ПЗ не формируют континуума чисел. Количество чисел конечно – 179 000 отрицательных и столько же положительных + 0.

И промежутки между невыражаемыми числами не постоянны: промежуток от 0.999*10 99 и 0.998 * 10 99 больше, чем промежуток от 0.999 * 10 0 до 0.998 * 10 0;

Итак, числа с ПЗ:

• используется специальный формат представления чисел,

• числа расположены неравномерно
по числовой оси,

• дискретность (расстояние между соседними числами) переменная
на всем диапазоне. Чем больше значения чисел, тем больше промежутки между ними.

 

8. Арифметические операции в формате с плавающей точкой.

При выполнении арифметических операций над числами, представленными в формате с плавающей точкой, надо отдельно выполнять их для порядков и мантисс.

При алгебраическом сложении чисел надо сначала уравнять порядки слагаемых.

При умножении порядки надо складывать, а мантиссы — перемножать.

При делении из порядка делимого вычитают порядок делителя, а над мантиссами совершают обычную операцию деления.

После выполнения операций, если это необходимо, проводят нормализацию результата, что влечет изменение порядков, т.к. каждый сдвиг на один разряд влево соответствует уменьшению порядка на единицу, а сдвиг вправо увеличению на единицу.

 

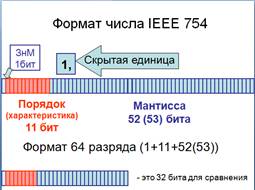
9. Стандарт IEEE 754.

До 80-х годов все производители компов представляли числа по-своему – несовместимость.

В конце 70-х все собрались и договорились до стандарта, который вышел в 1985 году.

Стандарт:

Предусматривает два формата для представления чисел с плавающей запятой: 32 -разрядные и 64 -разрядные.

Формат отводит самый старший бит под знак мантиссы, затем следует смещенный порядок (характеристика), потом мантисса (без скрытой единицы).

Для 32-битного формата это 1+8+23 разряда (смещение порядка 127).
Для 64-битного 1+11+52 (смещение 1023)

Диапазон чисел с плавающей запятой:
32 -разрядные –» ± 10 ^±38
64 -разрядные –» ± 10 ^±308

Формат 32 бита называется «одинарная точность» (single precision).

Формат 64 бита называется «двойная точность» (double precision).

Позже были введены 16 бит и 128 бит (половинная и учетверенная точность).

 

Кроме нормализованных чисел, в стандарте введены еще 4 типа:

- бесконечность, не число, нуль, ненормализованное число.

 

10. ФорматBCD. Представление текстовой информации ASCII

Двоично-десятичный код (англ. binary-coded decimal), BCD, 8421-BCD — форма записи рациональных чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода.

Например, десятичное число 311₁₀ будет записано в двоичной системе счисления в двоичном коде как 1 0011 0111₂, а в двоично-десятичном коде как 0011 0001 0001_BCD.

При помощи четырех бит можно закодировать шестнадцать цифр. Из них используются 10. Остальные 6 комбинаций в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр:

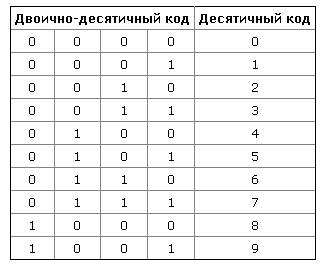
Двоично-десятичный код также применяется в телефонной связи. В этом случае кроме десятичных цифр кодируются символы '*' или '#' или любые другие. Для записи этих символов в двоично-десятичном коде используются запрещенные комбинации

 

Преимущества

· Упрощён вывод чисел на индикацию — вместо последовательного деления на 10 требуется просто вывести на индикацию каждый полубайт. Аналогично, проще ввод данных с цифровой клавиатуры.

· Для дробных чисел (как с фиксированной, так и с плавающей запятой) при переводе в человекочитаемый десятичный формат и наоборот не теряется точность.

· Упрощены умножение и деление на 10, а также округление.

По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.

Недостатки

· Требует больше памяти.

· Усложнены арифметические операции. Так как в 8421-BCD используются только 10 возможных комбинаций 4-х битового поля вместо 16, существуют запрещённые комбинации битов: 1010(10₁₀), 1011(11₁₀), 1100(12₁₀), 1101(13₁₀), 1110(14₁₀) и 1111(15₁₀).

 

Представление текстовой информации. ASCII

В современных ЭВМ, в зависимости от типа операционной системы и конкретных прикладных программ, используются 8-разрядные и 16-разрядные (Windows 95, 98, NT) коды символов.

Использование 8-разрядных кодов позволяет закодировать 256 различных знаков, этого вполне достаточно для представления многих символов, используемых на практике. При такой кодировке для кода символа достаточно выделить в памяти один байт. Так и делают: каждый символ представляют своим кодом, который записывают в один байт памяти.

В персональных компьютерах обычно используется система кодировки ASCII (American Standard Code for Information Interchange - американский стандартный код для обмена информации). Он введен в 1963 г. и ставит в соответствие каждому символу семиразрядный двоичный код. Легко определить, что в коде ASCII можно представить 128 символов.

В системе ASCII закреплены две таблицы кодирования базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.

Первые 32 кода базовой таблицы, начиная с нулевого, отданы производителям аппаратных средств. В этой области размещаются управляющие коды, которым не соответствуют ни какие символы языков.

Начиная с 32 по 127 код размещены коды символов английского алфавита, знаков препинания, арифметических действий и некоторых вспомогательных символов.

Кодировка символов русского языка, известная как кодировка Windows-1251, была введена "извне" - компанией Microsoft, но, учитывая широкое распространение операционных систем и других продуктов этой компании в России, она глубоко закрепилась и нашла широкое распространение.

Универсальная система кодирования текстовых данных.

Если проанализировать организационные трудности, связанные с созданием единой системы кодирования текстовых данных, то можно прийти к выводу, что они вызваны ограниченным набором кодов (256). В то же время, очевидно, что если, кодировать символы не восьмиразрядными двоичными числами, а числами с большим разрядом то и диапазон возможных значений кодов станет на много больше. Такая система, основанная на 16-разрядном кодировании символов, получила название универсальной - UNICODE. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65 536 различных символов - этого поля вполне достаточно для размещения в одной таблице символов большинства языков планеты.

11. Алгебра логики. Переменные и константы алгебры логики

Алгебра логики рассматривает высказывания и их взаимосвязь только с точки зрения их истинности либо ложности.

Если x – это высказывание, то в алгебре логики
x = True (x = Истина) либо x = False (x = Ложь)

Два элемента булевой алгебры, а именно событие истинно и событие ложно, называются ее константами. Будем понимать под ними значения соответственно лог. 1 и лог. 0.

Для упрощения записей значения «Ложь» и «Истина» обозначают нулем и единицей (0 и 1).

Логические переменные могут принимать только эти два значения.

Примеры: x = 0, x1 = 0, x2 = 1, y = 0, Alpha = 1

Переменные – как обычные переменные.

А вообще, булева алгебра оперирует ансамблями, где каждая из переменных либо 1 либо 0. Любое значение может быть представлено при помощи ансамбля.

12. Законы и аксиомы алгебры логики. Логические функции

Аксиомы алгебры логики:

Законы алгебры логики:

Законы рефлексивности

a ∨ a = a

a ∧ a = a

Законы коммутативности

a ∨ b = b ∨ a

a ∧ b = b ∧ a

Законы ассоциативности

(a ∧ b) ∧ c = a ∧ (b ∧ c)

(a ∨ b) ∨ c = a ∨ (b ∨ c)

Законы дистрибутивности

a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)

a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)

Закон отрицания отрицания

(a) = a

Законы де Моргана

(a ∧ b) = a ∨ b

(a ∨ b) = a ∧ b

Законы поглощения

a ∨ (a ∧ b) = a

a ∧ (a ∨ b) = a

 

Независимые высказывания называют аргументами. Высказывания, истинность либо ложность которых зависит от истинности либо ложности других высказываний, называют логическими функциями, зависящими от своих аргументов:

y = f(x), y = f(x1, x2, x3) и т.п.