Записати загальні математичні вирази для суми за станами системи (Z) і молекули (Q) та проаналізувати їх зміст. Довести, що для ідеального газу ці величини зв'язані співвідношенням
 . (1)
. (1)
На основі фундаментального рівняння статистичної термодинаміки, яке виражає енергію Гельмгольца системи через статистичну суму Z
 , (2)
, (2)
і рівняння (1) довести, що зв'язок термодинамічних властивостей ідеального газу з молекулярною сумою за станами може бути подано у вигляді:
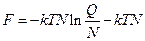 ; (3)
; (3)
 ; (4)
; (4)
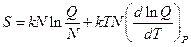 ; (5)
; (5)
 ; (6)
; (6)
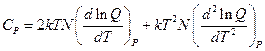 . (7)
. (7)
Завдання № 5/2. Розрахунок молекулярної суми за станами Q
2.1. Довести, що молекулярну суму за станами Q для ідеального газу може бути подано у вигляді добутку
 , (8)
, (8)
де Qпост. - сума за станами поступального руху; Qвн. - сума за внутрішньомолекулярними станами; ε0 - енергія молекули на нульовому енергетичному рівні.
2.2. Показати, що величину Qвн. у формулі (8) у свою чергу може бути представлено як добуток обертальної (Qоб.), коливальної (Qкол.) і електронної (Qел.) складових:
 . (9)
. (9)
2.3. З урахуванням (8) показати, що при виділенні нульової енергії формули (3) - (7) для 1 моля ідеального газу мають вигляд:
 ; (10)
; (10)
 ; (11)
; (11)
 ; (12)
; (12)
 ; (13)
; (13)
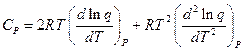 ; (14)
; (14)
2.4. Вивести формули для поступальної, обертальної та коливальної складових молекулярної суми за станами. Показати, що вони можуть мати вигляд:
 ; (15)
; (15)
для лінійних молекул:
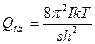 ; (16)
; (16)
для нелінійних молекул:
 ; (17)
; (17)
 , (18)
, (18)
де m - маса частинки; V - об'єм газу; І - момент інерції молекули; s- число симетрії; νi - частота і-го виду коливань.
2.5. Обчислити поступальні, коливальні та повні молекулярні суми за станами для певного ідеального газу. Об'єкт та температура для розрахунку задаються викладачем.
Завдання № 5/3. Розрахунок термодинамічних функцій ідеального газу статистичним методом
З використанням формул (10) - (18) обчислити значення функцій  ,
, 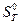 ,
,  і
і  для певного ідеального газу за температури, вказаної викладачем.
для певного ідеального газу за температури, вказаної викладачем.
Завдання № 5/4. Розрахунок констант хімічної рівноваги статистичним методом
Довести, що константу хімічної рівноваги для реакції  , яка протікає в газовій фазі, може бути обчислено за формулою:
, яка протікає в газовій фазі, може бути обчислено за формулою:
 , (19)
, (19)
де  - тепловий ефект реакції за абсолютного нуля; Δν - різниця стехіометричних коефіцієнтів.
- тепловий ефект реакції за абсолютного нуля; Δν - різниця стехіометричних коефіцієнтів.
З використанням цієї формули обчислити константу хімічної рівноваги для реакції, вказаної викладачем за певної температури.
ОСНОВИ ХІМІЧНОЇ КІНЕТИКИ
Основні поняття хімічної кінетики. Механізм реакції, прості та складні реакції. Швидкість реакції. Кінетичні криві. Кінетичні рівняння. Порядок реакції та методи його визначення. Константа швидкості реакції. Період напівперетворення. Молекулярність елементарних реакцій та її зв'язок з порядком реакції. Інтегрування кінетичних рівнянь для реакцій різних порядків.
Складні реакції. Паралельні реакції. Послідовні реакції. Метод стаціонарного стану. Оборотні реакції. Зв'язок між кінетикою та термодинамікою.
Молекулярно-кінетична теорія газів. Розподілення Максвелла-Больцмана. Середня та середньо-квадратична швидкості. Переріз зіткнення. Фактор зіткнення. Частота зіткнень. Довжина вільного пробігу.
Явища переносу в газах. Дифузія, теплопровідність, в'язкість газів. Ефузія. Теорія зіткнень в хімічній кінетиці. Активні зіткнення. Теорія Арреніуса. Залежність константи швидкості від температури, енергія активації та її експериментальне визначення.
Теорія перехідного стану (активного комплексу). Поверхня потенціальної енергії. Правило Поляні. Трансмісійний коефіцієнт. Статистичний розрахунок константи швидкості. Термодинамічний аспект теорії активного комплексу, ентропія активації.
Література: [1-7,9-11,14-16].






