Рассчитаем интегральную функцию F (t) нормального распределения для Х4 (износ винта), задавшись Тср =330000 час., d=500, определим аргумент функции Лапласа и занесем данные в табл. 10.
Таблица 10 - Сводная таблица расчета интегральной функции нормального распределения
| t´103, час. | |||||||||
| Х | -4 | -3 | -2 | -1 | |||||
| Ф(х) | -0,5 | -0,5 | -0,48 | -0,34 | 0,34 | 0,48 | 0,5 | 0,5 | |
| F(t) | 0,02 | 0,16 | 0,5 | 0,84 | 0,98 |
На основе расчетных данных таблицы 10 построим график нормального распределения (рисунок 8).
|
Рис. 8 – Интегральная функция нормального распределения
Полученную выборку 6´5 заносим в таблицу 11
Таблица 11 – Временная выборка из пяти реализаций для шести элементов t ´103
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 296 (4) | 299 (1) | 0,0028 | |||||||
| 294 (6) | 0,0033 | |||||||||
| 297 (3) | 299 (1) | 294 (6) | 296 (4) | 0,0078 | ||||||
| 299 (1) | 297 (3) | 0,0022 | ||||||||
| 294 (6) | 0,0033 | |||||||||
Итого: 0,0194
Полный коэффициент отказа элемента системы 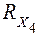 рассчитывается как
Его численное значение 
|
Моделирование износа чашки (X5), износа стержня (Х6), износа внутренней поверхности отстойника (Х8)
Рассчитаем интегральную функцию F (t) нормального распределения для Х5 (износ чашки), Х6 (износ стержня) и Х8 (износ внутренней поверхности отстойника), задавшись Тср =180000 час., d=500, определим аргумент функции Лапласа и занесем данные в табл. 12.
Таблица 12 - Сводная таблица расчета интегральной функции
нормального распределения
| t´103, час. | |||||||||
| Х | -4 | -3 | -2 | -1 | |||||
| Ф(х) | -0,5 | -0,5 | -0,48 | -0,34 | 0,34 | 0,48 | 0,5 | 0,5 | |
| F(t) | 0,02 | 0,16 | 0,5 | 0,84 | 0,98 |
На основе расчетных данных таблицы 12 построим график нормального распределения (рисунок 9).
|
Рис. 9 – Интегральная функция нормального распределения
Полученную выборку 6´5 заносим в таблицу 13
Таблица 13 – Временная выборка из пяти реализаций для шести элементов t ´103 для Х5
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 177 (3) | 179 (1) | 0,0036 | |||||||
| 176 (4) | 174 (6) | 0,0091 | ||||||||
| 176 (4) | 0,0036 | |||||||||
| 177 (3) | 0,0032 | |||||||||
| 176 (4) | 174 (6) | 178 (2) | 176 (4) | 178 (2) | 0,0168 | |||||
| Итого 0,0363 | ||||||||||
Полный коэффициент отказа элемента системы  рассчитывается как
Его численное значение 
|
Таблица 14 – Временная выборка из пяти реализаций для шести элементов t ´103 для Х6
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 176 (4) | 0,0037 | ||||||||
| 177 (3) | 174 (6) | 177 (3) | 0,011 | |||||||
| 176 (4) | 174 (6) | 178 (2) | 0,011 | |||||||
| 174 (6) | 177 (3) | 0,0083 | ||||||||
| 179 (1) | 0,0009 | |||||||||
Итого: 0,0349
Полный коэффициент отказа элемента системы  рассчитывается как
Его численное значение 
|
Таблица 15 – Временная выборка из пяти реализаций для шести элементов t ´103 для Х8
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 176 (4) | 179 (1) | 174 (6) | 0,01 | ||||||
| 178 (2) | 176 (4) | 0,0054 | ||||||||
| 174 (6) | 179 (1) | 0,0065 | ||||||||
| 177 (3) | 172 (8) | 176 (4) | 174 (6) | 0,0159 | ||||||
| 179 (1) | 0,0009 | |||||||||
Итого: 0,0387
Полный коэффициент отказа элемента системы  рассчитывается как
Его численное значение 
|
