Заклинивание клапана
Построю интегральную функцию экспоненциального распределения:
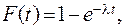(1.1)
где l — интенсивность отказов.
Интенсивность отказов рассчитывается по формуле:
1/час (1.2)
где Тср — среднее время наработки на отказ.
Приму среднюю наработку на отказ устройства при заклинивании клапана Тср =220000 часов.
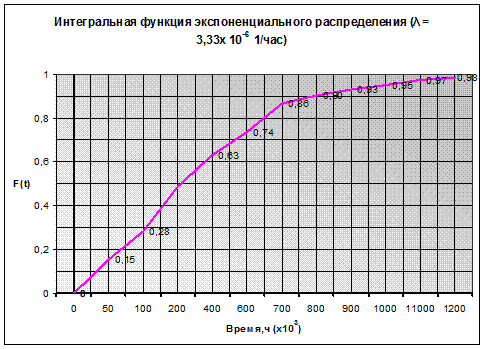
| F(55000)=0,22 | F(550000)=0,92 |
| F(110000)=0,39 | F(660000)=0,95 |
| F(330000)=0,78 | F(770000)=0,97 |
| F(440000)=0,86 | F(880000)=0,98 |
По расчетным данным построю интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 3¸4 раза больше Тср. На оси ординат — значение функции F (t).
|
Таблица 1 - Временная выборка из шести реализаций для восьми элементов t ´103 час
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||||
| Количество реализаций | 89 (21) | 98 (12) | 0,0177 | |||||||||
| 27,5 (82,5) | 65 (45) | 58 (52) | 179,5 | 1096,5 | 0,1637 | |||||||
| 75 (35) | 50 (60) | 0,0624 | ||||||||||
| 50 (60) | 83 (27) | 53 (57) | 50 (60) | 0,1140 | ||||||||
| 27,5 (82,5) | 67 (43) | 47 (63) | 28 (82) | 270,5 | 1638,5 | 0,1651 | ||||||
| 83 (27) | 75 (35) | 30 (80) | 42 (68) | 0,1974 | ||||||||
| Итого:0,7202 |
Далее временные значения ti, приведенные в таблице 1, сравню с Тср /2 = 110000, поскольку меня интересует поведение системы в первый полупериод эксплуатации. Затем получу время t 0 нерабочего состояния элемента системы Х1, выбирая лишь те случаи, когда ti < Тср /2. Расчет произведу по формуле
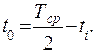(1.3)
Полученное значение t 0 занесу в таблицу 1, указав его в скобках, затем суммирую нерабочее время в единичной реализации t 0 и беру отношение к сумме общего времени tобщ работы элемента в этой реализации. На основе полученных значений определю вероятность отказа элемента системы Х1 для данной реализации по формуле:
(1.4)
и так для каждой реализации.
Вероятность отказа элемента системы Х1 является средним арифметическим этих значений:
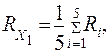(1.5)
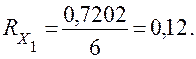
Разработка отверстий
Приму среднюю наработку на отказ устройства при разработки отверстий Тср =250000 часов.
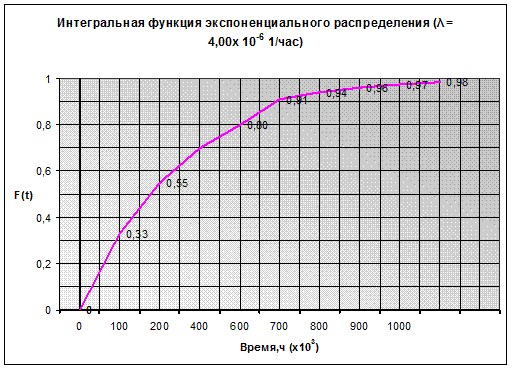
| F(100000)=0,33 | F(700000)=0,94 |
| F(300000)=0,7 | F(800000)=0,96 |
| F(500000)=0,86 | F(900000)=0,97 |
| F(600000)=0,91 | F(1000000)=0,98 |
По расчетным данным построю интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 3¸4 раза больше Тср. На оси ординат — значение функции F (t).
|
Таблица 2 - Временная выборка из шести реализаций для восьми элементов t ´103 час
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||||
| Количество реализаций | 115 (10) | 110 (15) | 0,0080 | |||||||||
| 50 (75) | 108 (17) | 0,0323 | ||||||||||
| 110 (15) | 100 (25) | 115 (10) | 0,0203 | |||||||||
| 35 (90) | 120 (5) | 0,0397 | ||||||||||
| Итого: 0,1003 |
Расчеты проведу аналогично п 1.1.1
Вероятность отказа элемента системы Х1
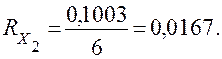
Моделирование постепенных отказов
Износ Гаек
Постепенные отказы подчиняются нормальному закону распределения. Интегральная функция нормального закона имеет вид:
(1.6)
где d - среднеквадратичное отклонение; a — математическое ожидание.
Для того, чтобы не рассчитывать интеграл, воспользуюсь половинной функцией Лапласа и с ее помощью рассчитаю нормальный закон распределения по формуле:
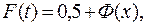(1.7)
где Ф (х) - половинная функция Лапласа; х =(t - Tср)/d, где
х - аргумент функции Лапласа;
t - время функционирования;
Тср - средняя наработка на отказ;
d - среднеквадратичное отклонение.
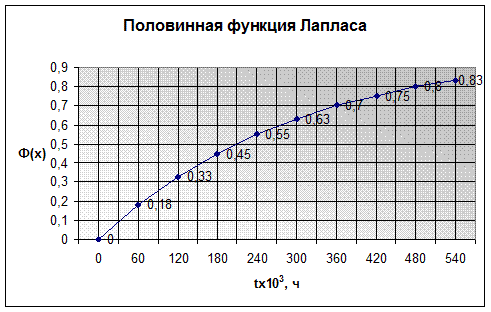
На рисунке 6 представлен график половинной функции Лапласа.
|
Рассчитаю интегральную функцию F (t) нормального распределения для Х3 (износ гаек), задавшись Тср =300000 час., d=154,92, определю аргумент функции Лапласа и занесу данные в табл. 3.
Таблица 3 - Сводная таблица расчета интегральной функции нормального распределения
| t´103, час. | |||||||||
| Х | -14,7 | -10,1 | -5,42 | -0,77 | 3,873 | 8,52 | 13,2 | 17,8 | 22,5 |
| Ф(х) | -0,64 | -0,34 | -0,1 | 0,1 | 0,26 | 0,4 | 0,5 | 0,6 | 0,66 |
| F(t) | 0,18 | 0,33 | 0,45 | 0,55 | 0,63 | 0,7 | 0,75 | 0,8 | 0,83 |
На основе расчетных данных таблицы 4 построю график нормального распределения (рисунок 7).
Процедура моделирования аналогична рассмотренной выше. Полученную выборку 8´6 занесу в таблицу 4.
Полученные в таблице 4 значения сравню с Тср, т. к. меня интересует характеристика системы в первый период эксплуатации. В тех случаях, если t 0< Tср, найду нерабочее время t 0 элемента системы Х3 по формуле 
. Полученное время указано в скобках в таблице 4. Затем, просуммировав время t 0 по реализации, беру отношение t 0 к суммарному времени функционирования элемента системы Х3 в этой реализации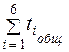 
. Вероятность отказа элемента системы Х3 в данной реализации определю по формуле (1.4):
|
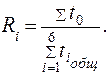
Полный коэффициент отказа элемента системы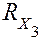 
рассчитывается как
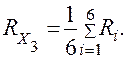
Его численное значение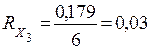 
Аналогично промоделирую для остальных гаек Х4, Х5, Х6. В данном примере получены такие значения: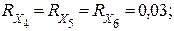 
Таблица 4- Временная выборка из 8´6 элементов
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||||
| Количество реализаций | 115 (35) | 108 (42) | 30 (120) | 0,079 | ||||||||
| 90 (60) | 0,017 | |||||||||||
| 145 (5) | 130 (20) | 50 (100) | 0,032 | |||||||||
| 106 (44) | 0,012 | |||||||||||
| 139 (11) | 30 (120) | 0,038 | ||||||||||
| Итого: 0,179 |
Износ Втулки
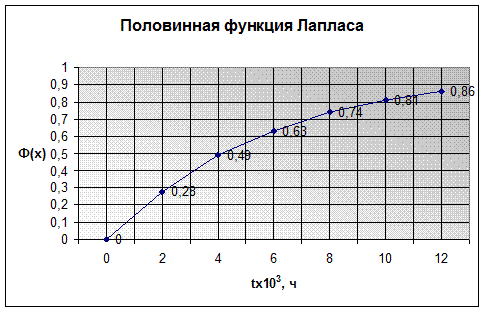
На рисунке 8 представлен график половинной функции Лапласа.
|
Рассчитаю интегральную функцию F (t) нормального распределения для Х7 (износ втулки), задавшись Тср =6000 час., d=3,53, определю аргумент функции Лапласа и занесу данные в табл. 3.
Таблица 5 - Сводная таблица расчета интегральной функции нормального распределения
| t´103, час. | |||||||
| Х | -0,43 | -0,27 | -0,12 | 0,04 | 0,19 | 0,35 | 0,5 |
| Ф(х) | -1 | -0,44 | -0,02 | 0,26 | 0,48 | 0,62 | 0,72 |
| F(t) | 0,28 | 0,49 | 0,63 | 0,74 | 0,81 | 0,86 |
На основе расчетных данных таблицы 6 построю график нормального распределения (рисунок 9).
Процедура моделирования аналогична рассмотренной выше. Полученную выборку 8´6 занесу в таблицу 6.
|
Полный коэффициент отказа элемента системы 
Таблица 6- Временная выборка из 8´6 элементов
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||||
| Количество реализаций | 0,67 (2,33) | 1,5 (1,5) | 8,6 | 3,5 | 2,15 (0,85) | 7,6 | 4,68 | 41,02 | 0,114 | |||
| 2,2 (0,8) | 1,77 (1,33) | 8,9 | 5,4 | 2,13 | 56,27 | 0,038 | ||||||
| 5,3 | 1,8 (1,2) | 4,7 | 1,35 (1,65) | 3,5 | 2,85 | 43,65 | 0,065 | |||||
| 6,5 | 4,3 | 5,4 | 2,5 (0,5) | 0,5 | 39,7 | 0,013 | ||||||
| 8,7 | 0,75 (2,25) | 1,88 (1,12) | 3,5 | 6,9 | 3,37 | 42,73 | 0,079 | |||||
| 2 (1) | 6,9 | 8,3 | 52,2 | 0,019 | ||||||||
| Итого:0,328 |
Износ набивки
На рисунке 10 представлен график половинной функции Лапласа.
|
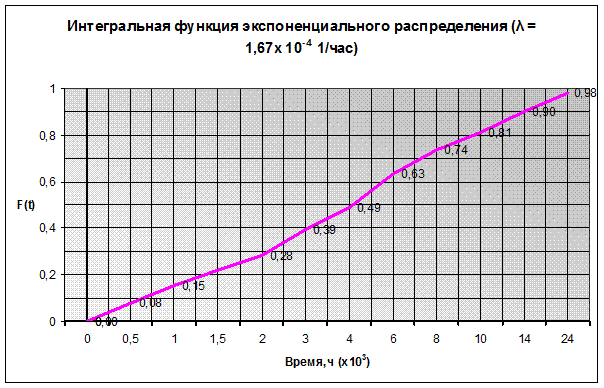
Рассчитаю интегральную функцию F (t) нормального распределения для Х8 (износ набивки), задавшись Тср =5000 час., d=2,58, определю аргумент функции Лапласа и занесу данные в табл. 7.
Таблица 7 - Сводная таблица расчета интегральной функции нормального распределения
| t´103, час. | |||||||||
| Х | -0,27 | -0,19 | -0,12 | -0,04 | 0,0387 | 0,12 | 0,19 | 0,27 | 0,35 |
| Ф(х) | -0,64 | -0,34 | -0,1 | 0,1 | 0,26 | 0,4 | 0,5 | 0,6 | 0,66 |
| F(t) | 0,18 | 0,33 | 0,45 | 0,55 | 0,63 | 0,7 | 0,75 | 0,8 | 0,83 |
На основе расчетных данных таблицы 7 построю график нормального распределения (рисунок 11).
Процедура моделирования аналогична рассмотренной выше. Полученную выборку 8´6 занесу в таблицу 8.
|
Полный коэффициент отказа элемента системы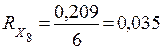 
Таблица 8- Временная выборка из 8´6 элементов
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||||
| Количество реализаций | 0,5 (2) | 1,75 (0,75) | 6,5 | 14,5 | 2 (0,5) | 3,25 | 40,25 | 0,081 | ||||
| 4,5 | 6,5 | 1,7 (0,8) | 8,5 | 2 (0,5) | 3,6 | 1,3 | 34,8 | 0,037 | ||||
| 2 (0,5) | 2,5 | 7,75 | 1 (1,5) | 2,5 | 50,75 | 0,039 | ||||||
| 11,5 | 1,25 (1,25) | 4,15 | 5,25 | 3,1 | 2,9 | 1,25 | 39,15 | 0,032 | ||||
| 3,75 | 2,25 (0,25) | 7,75 | 1,78 (0,72) | 3,7 | 0,97 | 49,23 | 0,020 | |||||
| 9,6 | 2,5 | 6,5 | 55,6 | |||||||||
| Итого:0,209 |
