Ателіктер теориясына кіріспе

1.1.1 ӨЛШЕУ КЕЗІНДЕГІ ҚАТЕЛІКТЕР

 

Мүлт кетушілік құралдың көрсетуіне ұқыпсыз қараушылықтан болады. Есептеу кезінде мұндай шамаларды алып тастау керек.

Кездейсоқ қателіктер өлшеу кезінде дәл байқамаушылықтан пайда болады. Мұның себебі біздің бақылау мүшелеріміздің және құралдардың идеал абсолютті еместігінен болады. Кездейсоқ қателіктер ықтималдық заңына бағынады, яғни бір өлшеуде нәтиже нақты мәннен үлкен, ал екінші өлшеуде нақты мәннен кіші болуы мүмкін. Кездейсоқ қателіктен құтылуға болмайды. Бірақ бірнеше рет қайталап өлшеу арқылы кездейсоқ қателіктің ықтималдық шамаларын анықтап ізделініп отырған шаманың аймағын есептеуге болады. Айталық бір физикалық шаманы өлшеудің нәтижесінде алдық дейік. Осылардың орташа арифметикалық шамасы: Жеке өлшеулердің абсолюттік қателіктері .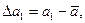

Бірнеше өлшеулер сериясының орташа квадраттық қателігі былай анықталады:

(1.1.1)

 

ӨЛШЕУЛЕРДІҢ МАТЕМАТИКАЛЫҚ ӨҢДЕУІ

 

2. Өлшеудің мәндері кестеге таблицаға жазылуы керек

3. Өлшеулердің орташа мәні:

4. Жеке өлшеулердің абсолюттік қателіктерінің квадраты анықталады:

5. Жеке өлшеулердің абсолюттік қателіктерінің квадраты анықталынады: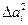

6. Бірнеше өлшеулердің орташа квадраттық қателігі анықталады:

7. Сенімділік ықтималдығы 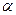берілуі керек

8. Сенімділік ықтималдығы 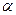және өлшеулер саны арқылы Стьюдент

коэффициенті кестеден алынады

9. Өлшеулердің қателігі анықталады

10. Соңғы нәтиже былай жазылады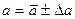

11. Салыстырмалы қателік анықталынады.

Стьюдент коэффициенті

1-кесте

Өлшеулер саны	Сенімділік ықтималдығы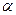
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99
	0,77	0,98	1,2	1,6	2,4	3,2	4,5	5,8
	0,74	0,94	1,2	1,5	2,1	2,8	3,7	4,6
	0,73	0,92	1,2	1,5	2,0	2,6	3,4	4,0
	0,72	0,90	1,1	1,4	1,9	2,4	3,1	3,7
	0,71	0,90	1,1	1,4	1,9	2,4	3,0	3,5
	0,71	0,89	1,1	1,4	1,8	2,3	2,9	3,4
	0,70	0,88	1,1	1,4	1,8	2,3	2,8	3,3
	0,69	0,87	1,1	1,3	1,8	2,1	2,6	3,0
	0,69	0,86	1,1	1,3	1,7	2,1	2,5	2,9

 

1.3 Жанама өлшеулердің қателіктері.

а) берілген функция логарифмделеді;

б) бұдан соң дифференциалданады;

в) орнына жазылады.

Жанама өлшеулердің абсолюттік қателігі функцияны дифференциалдау арқылы анықталады.

Мынадай мысалды қарастырайық:

1. Параллепипедтің көлемінің өлшеулері 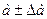, , болсын, және анықтау керек болсын.

(1.1.2)

Абсолюттік қателік анықтайық. Ол үшін (1.1.2) өрнекті дифференциалдау керек.

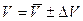
салыстырмалы қателікті анықтау үшін өрнекті логарифмдейік:

мұны дифференциалдайық

Енді орнына қоямыз.

 

2. Өлшеулер нәтижесі шардың радиусының мынадай мәндерін көрсетті: Шардың көлемін анықтау керек. Шардың көлемі

Абсолюттік қателік:

(1.1.3)

Салыстырмалы қателік:

Радиустың арифметикалық орта мәні:

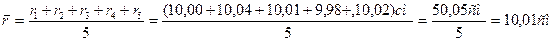
Кесте құрайық

2-кесте

 

№
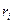
	10,01
	10,02	0,01	0,0001
	9,98	0,03	0,009
	10,04	0,03	0,0009
	10,00	0,01	0,0001

 

Орташа квадраттық қателік:

Сенімділік болғанда Стьюдент коэффициенті болады (кестеден алынады) өлшеудің қателігі .

Егер Х - шамасы жанама өлшенетін болса, онда оның өлшеу нәтижесі х – тура өлшенген бір немесе бірнеше айнымалының функциясы болады.

 

Әртүрлі нұсқаны қарастырайық.

а) х – бір айнымалының функциясы.

Ендеше А шамасының тура өлшеу нәтижесі а болсын, осы нәтиженің қателігі белгілі және ол 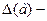ға тең болсын. Сонымен делік, ендеше ті табу керек. және өте аз шамалар деп есептеп, және 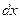дифференциалдарды байланыстыратын мына өрнекті пайдалануға болады:

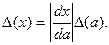(1.1.4)

Бұл жердегі модуль белгісінің қойылуының себебі дифференциалдарға қарағанда қателіктер әрқашан оң.

(1.1.4) - ші өрнекке байланысты мысалдар 3-ші кестеге енгізілген.

Кейбір жанама өлшеулердің қателіктері.

 

3-кесте.

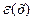х(а) - функциясының түрі	абсолюттік қателік	салыстырмалы қателік

 

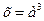
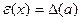
б) х – бірнеше айнымалының функциясы.

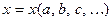болсын, мұндағы - шамаларының тура өлшеу нәтижелері. Осы нәтижелердің қателіктері белгілі, олар тең. ті табу керек. Осы есепті шешу жолы келесі өрнекпен беріледі

(1.1.5)

мұндағы және т.б. – дербес қателіктер, олар (1.1.5) – ге сәйкес:

, (1.1.6)

(1.1.5) және (1.1.6) өрнектерге мысалдар 4-ші кестеде көрсетілген.

 

4-кесте.

Функция түрі	Абсолюттік қателік	Салыстырмалылы қателік

 

Ескерту. Осы пунктте келтірілген өрнектер барлық түрдегі қателіктер үшін дұрыс – құралдың, кездейсоқ және толық қателіктер. Көбінесе оларды толық қателіктер үшін пайдаланады – алдымен тура өлшеу үшін құралдан кеткен қатені, кездейсоқ және толық қателіктерді, содан кейін – жанама өлшеудің толық қателігін табады.