Основная задача - установить закономерность падения давления по длине трубопровода и получить зависимость массового расхода газа от начального и конечного давлений.
Для рассматриваемого случая исходными являются: уравнения Бернулли в механической форме
(9.1)
уравнение неразрывности (расхода)
(9.2)
уравнение состояния
(9.3)
уравнение термодинамического процесса
(9.4)
Потери напора на гидравлические сопротивления распишем по формуле Дарси-Вейсбаха
(9.5)
где 
- коэффициент гидравлических сопротивлений по длине газопровода;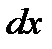 
- элемент длины газопровода; 
- внутренний диаметр труб.
Покажем, что 
для изотермического движения газа является константой. Известно, что в общем случае 
. Т.к. относительная шероховатость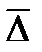 
душ заданного трубопровода имеет конкретное значение, то 
. Но число 
, определяемое по формуле
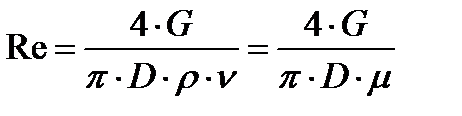(9.6)
практически не изменяется по длине газопровода. Действительно, для рассматриваемого случая 
, а динамическая вязкость газа 
в диапазоне давлений до 10 МПа практически зависит только от температуры (а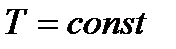 
).
Решая (9.1) относительно 
, получим с учетом (9.5)
(9.7)
Из этого уравнения видно, что падение давления в газопроводе складывается из потерь давления на трение, на подъем газа по вертикали и на изменение кинетической энергии. Для случая горизонтальных труб dz = 0. Преобразуем уравнение (9.7) к виду удобному для интегрирования. Для этого умножим обе части уравнения на 
и воспользуемся преобразованием
(9.8)
Тогда получим
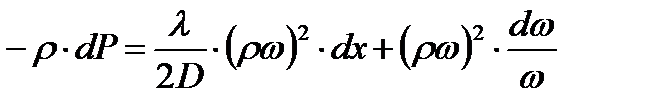(9.9)
которое можно представить еще иначе, если воспользоваться равенством (9.4)
(9.10)
Интегрирование (9.10) дает
(9.11)
где С - константа интегрирования, которая находится из граничных условий. Например, если известны параметры в начале трубопровода 
, то
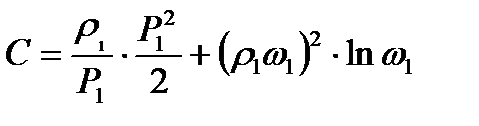
Тогда уравнение (9.11) примет вид
(9.12)
которое представляет собой закон распределение давления по длине трубопровода. В частном случае, когда известно давление в конце газопровода 
, имеем
(9.13)
но, согласно (9.2) - (9.4)
(9.14)
Решая (9.13) относительно массовой скорости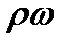 
, с учетом (9.14), получим
Тогда искомое выражение для массового расхода примет вид
(9.15)
Можно показать, что для магистральных газопроводов справедливо неравенство
(9.16)
Тогда, пренебрегая в выражении (9.15) членом 
получим окончательно
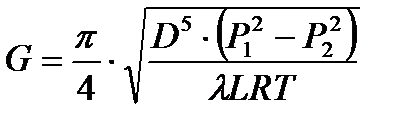(9.17)
Формулой (9.17) пользуются при газодинамическом расчете изотермических газопроводов. Причем для вычисления коэффициента гидравлического сопротивления по длине газопровода можно пользоваться известными формулами Альтшуля, Никурадзе и т.д.
С учетом проведенной оценки (9.16) выражение (9.1) примет вид
(9.18)
Из (9.17) имеем
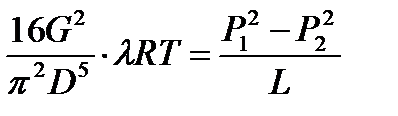
тогда, с учетом этого равенства, закон распределения давления по длине газопровода (9.18) примет более простой вид
(9.19)
Зависимость 
по формуле (9.19) можно представить графически в координатах 
(рис. 9.1) и в координатах 
(рис. 9.2). Таким образом, согласно (9.19) давление по длине газопровода падает по параболическому закону.
Рис. 9.1 График падения давления по длине газопровода
Рис. 9.2 Зависимость падения квадрата давления по длине газопровода
