Закон изменения момента количества движения

Этот закон формулируется следующим образом. Сумма мо­ментов импульсов всех внешних сил относительно некоторой точки 0 равна изменению суммарного момента количества дви­жения рассматриваемой системы материальных точек за то же время, причем моменты количества движения берутся относи­тельно той же точки 0. Математически этот закон записыва­ется так

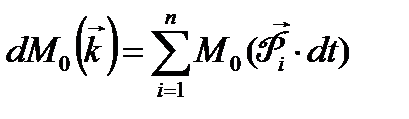(2.9)

где 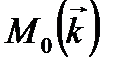- момент количества движения системы материаль­ных точек относительно точки 0; - изменение этого момента; - импульс i -ой внешней силы; момент импульса; -ой внешней силы относи­тельно точки 0.

Преобразуем выражение (2.9) применительно к газовому потоку. Дня этого выделим часть потока газа, заключенного между контрольными сечениями 1 и 2 (рис. 2.3), в некоторый момент времени ,

 

 

Рис. 2.3 К выводу закона измене­ния момента количества движения

 

За время выделенная масса газа займет новое по­ложение 1'-2' (рис. 2.2). Рассмотрим частный случай, когда движение установившееся. Тогда можно показать (так же как и в предыдущем параграфе), что изменение момента количества движения отсека 1-2 за время определяется как разница моментов количества движения отсеков 2-2' и 1-1'.

Момент количества движения определяется как векторное произведение , в котором - радиус-вектор, соединяющий рассматриваемое сечение с точкой 0, относитель­но которой вычисляется момент.

Учитывая изложенное, закон (2.9) можно записать для отсека потока газа 1-2 в виде

(2.10)

Согласно уравнению расхода (2.5'), масса отсеков 1-1' и 2-2' одинакова и равна

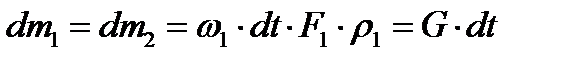
Вынося общий множитель и сокращая обе части равенства (2.10) на , получим

(2.11)

Из курса математики известно, что векторное произведе­ние двух векторов представляет собой вектор, направленный перпендикулярно плоскости (обозначим это направление через ), модуль этого вектора равен произведению , где 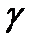- угол между 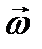и Учитывая это, векторное уравнение (2.11) в проекции на ось дает

(2.12)

где , - тангенсальная составляющая скоростей и соответственно;

Уравнение (2.12) и представляет собой закон измене­ния момента количества движения применительно к установив­шемуся потоку сжимаемой среды (газа). Оно получило назва­ние турбинного уравнения Эйлера, которое широко использу­ется в теории центробежных машин.

Закон сохранения энергии

Закон сохранения полной энергии является одним из фун­даментальных законов физики. Применительно к газовой ди­намике этот закон рассмотрим для одной и той же массы газа, заполнявшей вначале объем 1-2 (рис. 2.2), а через беско­нечно малый промежуток времени 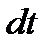переместившейся в по­ложение 1' - 2'.

Согласно закону сохранения энергии следует, что подво­димая к рассматриваемой массе газа за время 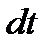тепловая энергия расходуется на совершение работы и на изменение по­тенциальной, кинетической и внутренней энергии газа.

Рассмотрим случай установившегося движения. Ввиду того, что отсек 1' - 2 (рис. 2.2) является общим для отсеков 1-2 и 1'-2' и, кроме того, энергия, как и масса газа этого отсека, не изменяется (для установившегося движения), то изменение энергии рассматриваемой массы газа определяется разностью энергий газа в отсеках 2-2' и 1-1'.

Из курса гидравлики известно, что и представ­ляют собой удельные потенциальные энергии положения и давления соответственно, а - удельную кинетическую энергию. Слово "удельная" означает, что энергия отнесена к единице массы, т.е. энергия, которую несет в себе каждый килограмм массы газа. Поэтому для определения энергии отсеков газа 1-1' и 2-2' необходимо удельную энергию умножить на массу этих отсеков

Следовательно, изменение потенциальной энергии рассматриваемой массы газа за время определяется

(2.13)

где , - нивелирная отметка сечений 1-1 и 2-2.

Изменение кинетической энергии равно:

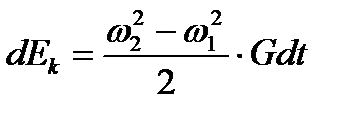(2.14)

Для изменения внутренней (тепловой) энергии можно записать:

,

которое с учетом выражения (1.5) можно переписать иначе:

(2.15)

Работа, которую совершает газ, состоит из работы на преодоление сил трения и технической работы (полез­ной) . Причем последняя может рассматриваться как положительная (например, работа газа по вращению колеса турбины), так и отрицательная (при прохождении газа через компрессор).

Закон сохранения энергии с учетом вышеизложенного мож­но записать математически:

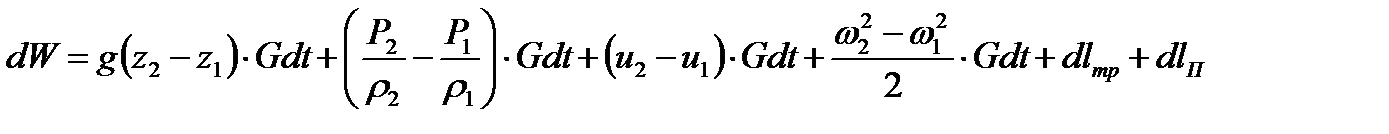
где dW - тепло, подводимое к газу массой .

Это выражение представим иначе, разделив все члены на величину , тем самым получаем уравнение энергии для единицы массы (1кг) газа:

(2.16)

где - тепло, подводимое к 1 кг газа на участке 1-2, 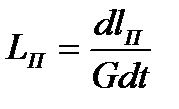- техническая работа, совершаемая 1 кг газа на том же участке; - работа сил трения, приходящаяся на 1 кг газа.

Приток тепла в общем случае осуществляется двумя спо­собами: извне - за счет теплообмена через боко­вую поверхность потока, изнутри - за счет преобра­зования в тепло работы трения, т.е.

(2.17)

Причем очевидно, что в точности равна энергии расходуемой газом на совершение работы трения

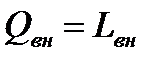(2.18)

Учитывая (2.17) и (2.18), уравнение энергии (2.16) можно переписать

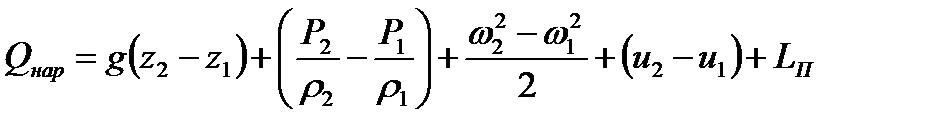(2.19)

которому можно придать другую форму, если воспользоваться выражением (1.12) для энтальпии

(2.20)

Если газ не совершает технической работы (или над га­зом не совершается работа), то и выражение (2.20) примет вид

(2.21)

Следует отметить, что уравнение энергии в форме (2.19), (2.20) и (2.21) не содержит работы трения. В самом деле, поскольку энергия, расходуемая на преодоление трения, преобразуется полностью в тепло, а последнее остает­ся в газовом потоке, наличие сил трения не может нарушить общий баланс энергии, а лишь приводит к преобразованию од­ного вида энергии в другой.

Уравнение (2.21) называют еще уравнением Бернулли в тепловой форме. Оно выражает собой баланс энергии в про­цессе движения и теплообмена с внешней средой, сопровождае­мые изменением состояния газа. Уравнение (2.21) можно вы­вести и из известного в гидравлике уравнения Бернулли (в механической форме)

(2.22)

где 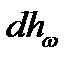- потеря напора на участке потока длиной , использовав при этом выражения (1.8) и (1.12).