Основные свойства газа
Изложение данного курса основано на представлении газа как сплошной сжимаемой среды. Среда называется сплошной, если имеет достаточно большое число молекул в бесконечно малом объеме занимаемого пространства. Это позволяет рассматривать такие параметры, как плотность газа, давление, скорость и температуру как непрерывные функции координат и, следовательно, широко применять аппарат математического анализа.
Термодинамическое состояние газа определяется тремя величинами: давлением  , плотностью
, плотностью  и температурой
и температурой  . Все эти параметры взаимосвязаны. Изменение какой-либо из этих величин приводит в общем случае к изменению остальных. Математическая зависимость указанных параметров называется уравнением состояния сжимаемой среды
. Все эти параметры взаимосвязаны. Изменение какой-либо из этих величин приводит в общем случае к изменению остальных. Математическая зависимость указанных параметров называется уравнением состояния сжимаемой среды
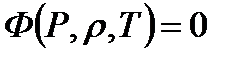 (1.1)
(1.1)
Иногда вместо плотности газа вводят понятие удельного объема  , представляющего собой величину, обратную плотности, т.е.
, представляющего собой величину, обратную плотности, т.е.
 (1.2)
(1.2)
В термодинамике в качестве уравнения состояния газа широко используется уравнение Клапейрона-Менделеева
 (1.3)
(1.3)
где  - газовая постоянная (для каждого газа своя), Дж/(кг
- газовая постоянная (для каждого газа своя), Дж/(кг  К). Значение
К). Значение  для каждого газа можно вычислить, если известна его молекулярная масса
для каждого газа можно вычислить, если известна его молекулярная масса  (кмоль/кг), по формуле:
(кмоль/кг), по формуле:
 (1.4)
(1.4)
где 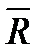 - универсальная газовая постоянная,
- универсальная газовая постоянная, 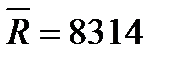 Дж/(кмоль
Дж/(кмоль  К).
К).
Уравнение состояния (1.3) получено теоретически для модели идеального газа, т.е. газа, в котором отсутствуют силы притяжения между молекулами и изменение внутренней энергии  связано только с изменением его абсолютной температуры
связано только с изменением его абсолютной температуры  . Для единицы массы газа это изменение определяется по формуле:
. Для единицы массы газа это изменение определяется по формуле:
 (1.5)
(1.5)
где  -удельная теплоемкость газа при постоянном объеме, Дж/(кг
-удельная теплоемкость газа при постоянном объеме, Дж/(кг  К).
К).
Для реальных сжимаемых сред внутренняя энергия  зависит не только от температуры, но и от давления, и соотношение (1.5) теряет силу.
зависит не только от температуры, но и от давления, и соотношение (1.5) теряет силу.
Именно поэтому газ, подчиняющийся уравнению вида (1.3), называют идеальным (в специальной литературе по газовой динамике такой газ называют еще совершенным). В газодинамике вводят также понятие идеальный газ в смысле невязкий (по аналогии с моделью идеальной жидкости), т.е. газ, у которого отсутствуют силы внутреннего трения. Поэтому, когда используется этот термин, необходимо четко различать какая из этих моделей имеется в виду.
Во избежание путаницы будем в дальнейшем пользоваться первым определением идеального газа, различая при этом отдельно случаи невязкого и вязкого газа.
Реальные газы, в общем случае, не следуют закону Клапейрона-Менделеева. Это уравнение с достаточной точностью может быть применено для реальных газов только в узком диапазоне изменения температуры и давления. Причем этот диапазон для каждого газа свой.
В настоящее время предложено множество эмпирических и полуэмпирических уравнений состояния для реальных газов. Наиболее известные из них - это уравнение Ван дер Ваальса и нижеследующее уравнение
 (1.6)
(1.6)
которое широко применяется в большинстве задач нефтяной и газовой отраслях промышленности.
В уравнении (1.6)  - коэффициент, учитывающий степень отклонения реального газа от идеального (совершенного), принимает значение меньшее, равное и большее единицы. Иногда
- коэффициент, учитывающий степень отклонения реального газа от идеального (совершенного), принимает значение меньшее, равное и большее единицы. Иногда  называют коэффициентом сжимаемости или сверхсжимаемости. Коэффициент
называют коэффициентом сжимаемости или сверхсжимаемости. Коэффициент  , вообще говоря, является функцией давления
, вообще говоря, является функцией давления 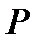 и температуры
и температуры  . Для нахождения численных значений
. Для нахождения численных значений  можно рекомендовать обобщенные графики, на которых
можно рекомендовать обобщенные графики, на которых  представлен в зависимости от приведенных значений давления
представлен в зависимости от приведенных значений давления 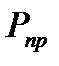 и температуры
и температуры 
 (1.7)
(1.7)
где 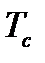 и
и  - критические температура и давление, являющиеся физико-химическими характеристиками газа.
- критические температура и давление, являющиеся физико-химическими характеристиками газа.
Известно, что изменяя  и
и  можно осуществлять фазовый переход вещества из газообразного в жидкое состояние, но не всегда.
можно осуществлять фазовый переход вещества из газообразного в жидкое состояние, но не всегда.
Критическая температура - это температура, выше которой газ невозможно перевести в жидкое состояние никаким (сколь угодно большим) повышением давления, т.е. при  газ еще можно обратить в жидкость. Минимальное давление, которое обеспечивает переход из газообразного состояния в жидкое при
газ еще можно обратить в жидкость. Минимальное давление, которое обеспечивает переход из газообразного состояния в жидкое при  , называется критическим
, называется критическим  .
.
Для каждого индивидуального (чистого) газа значение  и
и  можно найти в специальной литературе по добыче, транспорту и переработке природного и нефтяного газа. Для газовых смесей вводятся понятия псевдокритических значений давления и температуры, определяемых через
можно найти в специальной литературе по добыче, транспорту и переработке природного и нефтяного газа. Для газовых смесей вводятся понятия псевдокритических значений давления и температуры, определяемых через  и
и  входных в смесь компонентов как средневзвешенные значения.
входных в смесь компонентов как средневзвешенные значения.
Основные сведения из термодинамики
Первое начало термодинамики представляет собой частную форму применительно к тепловым процессам всеобщего закона природы - закона превращения и сохранения энергии. Для квазистатических процессов он формулируется следующим образом: подведенное к единице массы газа бесконечно малое количество тепла 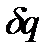 расходуется на повышение внутренней энергии газа
расходуется на повышение внутренней энергии газа  и на выполнение термодинамической работы
и на выполнение термодинамической работы
 (1.8)
(1.8)
где  - удельный объем, определяемый по формуле (1.2).
- удельный объем, определяемый по формуле (1.2).
Формальное интегрирование выражения (1.8) позволяет найти полное количество тепла, которое подведено к газу в процессе изменения его состояния от начального 1 до конечного2.
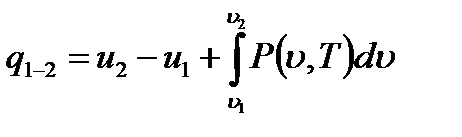 (1.9)
(1.9)
Интеграл, стоящий в правой части равенства (1.9), представляет работу термодинамического процесса расширения и зависит от характера процесса, т.е. вида кривой, соединяющей точки 1 и 2 на поверхности 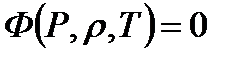 . Это указывает на то, что
. Это указывает на то, что 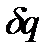 , входящее в равенство (1.8), не является полным дифференциалом. Однако, если обе части равенства (1.8) умножить на интегрирующий множитель
, входящее в равенство (1.8), не является полным дифференциалом. Однако, если обе части равенства (1.8) умножить на интегрирующий множитель  , то выражение
, то выражение  становится полным дифференциалом некоторой функции состояния
становится полным дифференциалом некоторой функции состояния  , называемой энтропией, т.е.
, называемой энтропией, т.е.
 (1.10)
(1.10)
При переходе газа из состояния 1 в состояние 2 изменение  не зависит от характера процесса перехода, а целиком и полностью определяется начальным и конечным состояниями.
не зависит от характера процесса перехода, а целиком и полностью определяется начальным и конечным состояниями.
Следует обратить внимание, что равенство (1.10) справедливо для обратимых процессов. Обратимым называется процесс изменения состояния, который, будучи переведен в обратном направлении, возвращает систему в первоначальное состояние через теже промежуточные состояния без каких- либо изменений в окружающей среде.
Необратимые процессы изменения состояния определяются условием
 (1.11)
(1.11)
Неравенство (1.11) является математическим выражением второго начала термодинамики, которое характеризует направление протекающих в природе макроскопических процессов. Второе начало термодинамики позволяет установить количественное соотношение между работой, которая могла бы быть совершена системой при обратимом процессе, и действительной работой.
При изучении закономерностей движения газа необходимо учитывать термодинамический процесс изменения состояния газа. При этом различают изотермический, адиабатный, изоэнтропийный, изоэнтальпийный процессы.
Процесс, происходящий без теплообмена системы с окружающей средой, называется адиабатным. Процесс в системе, при котором сохраняется неизменной энтропия системы, называется изоэнтропийным. Изоэнтропийный процесс - это не что иное как обратимый адиабатный процесс. Он возможен в энергетически изолированной системе при отсутствии трения между частицами газа. При наличии трения между частицами газа адиабатный процесс будет неизоэнтропийным. Выделяющееся внутри системы тепло, обусловленное работой сил трения приводит к возрастанию энтропии  и, конечно, процесс при этом будет необратимым.
и, конечно, процесс при этом будет необратимым.
Процесс в системе, характеризуемый постоянством энтальпии, называется изоэнтальпийным.
Энтальпией (теплосодержанием), отнесенной к единице массы, называется функция
 (1.12)
(1.12)
которая определяется только состоянием газа, например, температурой и давлением.
Рассмотрим основные соотношения термодинамических параметров для идеального газа, которые будут использоваться в дальнейшем при изложении курса.
Подведенное к системе тепло 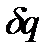 приведет к новому состоянию газа с параметрами
приведет к новому состоянию газа с параметрами  . Количество подведенного тепла
. Количество подведенного тепла 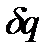 можно выразить через удельную теплоемкость газа при постоянном давлении
можно выразить через удельную теплоемкость газа при постоянном давлении 

 (1.13)
(1.13)
С другой стороны, согласно первому началу термодинамики подведенное тепло идет на изменение внутренней энергии газа, которое в соответствии с (1.5) равно  , и на выполнение работы расширения газа
, и на выполнение работы расширения газа  . Следовательно,
. Следовательно,
 (1.14)
(1.14)
Второе слагаемое в правой части равенства (1.14) можно преобразовать, используя уравнение состояния (1.3), к виду
 (1.15)
(1.15)
Если теперь заменить второе слагаемое в (1.14) по формуле (1.15), то после сокращения на величину  получим известное в термодинамике выражение Майера
получим известное в термодинамике выражение Майера
 (1.16)
(1.16)
Используя соотношения (1.3), (1.5) и (1.16), можно получить иные выражения для энтальпии  . В самом деле, из (1.12) имеем
. В самом деле, из (1.12) имеем
 (1.17)
(1.17)
Последнее выражение предстанет в ином виде, если в нем заменить  по формуле (1.3)
по формуле (1.3)
 (1.18)
(1.18)
где 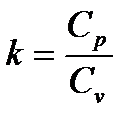 (1.19)
(1.19)
Изменение энтропии  при переходе идеального газа из состояния 1 в состояние 2 определится интегрированием (1.10), которое с учетом выражений (1.5) и (1.3) дает
при переходе идеального газа из состояния 1 в состояние 2 определится интегрированием (1.10), которое с учетом выражений (1.5) и (1.3) дает

или, если использовать формулу Майера (1.16)
 (1.20)
(1.20)
Используя (1.20), получается уравнение адиабаты Пуассона, описывающее изоэнтропийный (обратимый адиабатный) процесс изменения состояния газа 
 (1.21)
(1.21)
Показатель степени  , входящий в (1.21) и определяемый формулой (1.19), называется показателем адиабаты Пуассона.
, входящий в (1.21) и определяемый формулой (1.19), называется показателем адиабаты Пуассона.
2. ОСНОВНЫЕ ЗАКОНЫ СЖИМАЕМОЙ СРЕДЫ
Вводные замечания
Движение любой сжимаемой среды характеризуется следующими физическими величинами: скоростью движения, плотностью среды, температурой и давлением. Причем в самом общем случае все эти величины взаимосвязаны. Изменение какой-либо одной из них автоматически приводит к изменению всех остальных. Связь указанных величин описывается математически уравнениями, которые получаются из общих фундаментальных законов физики, механики, термодинамики. С отдельными соотношениями - уравнением состояния и уравнением термодинамического процесса - уже знакомы. Эти уравнения справедливы как для покоя, так и для движения, Однако в случае движения сжимаемой среды этих уравнений недостаточно для решения инженерных задач. К ним необходимо добавить уравнения, содержащие скорость движения, которые получаются при применении законов сохранения массы и энергии, законов изменения количества движения и момента количества движения к движущейся сжимаемой среде.
В виду того, что в большинстве задач инженерной практики трубопроводного транспорта газа приходится иметь дело с одномерными течениями, а также из-за ограниченности объема настоящего пособия, изложение основных законов движения сжимаемой среды дается применительно к одномерным потокам конечных размеров. Хотя можно было бы (так же, как и в курсе гидравлики) сначала рассмотреть основные законы газодинамики в самом общем (трехмерном) случае, а затем с помощью элементарной струйки распространить их на поток конечных размеров введением средней* (по сечению потока) скорости  .
.
Закон сохранения массы
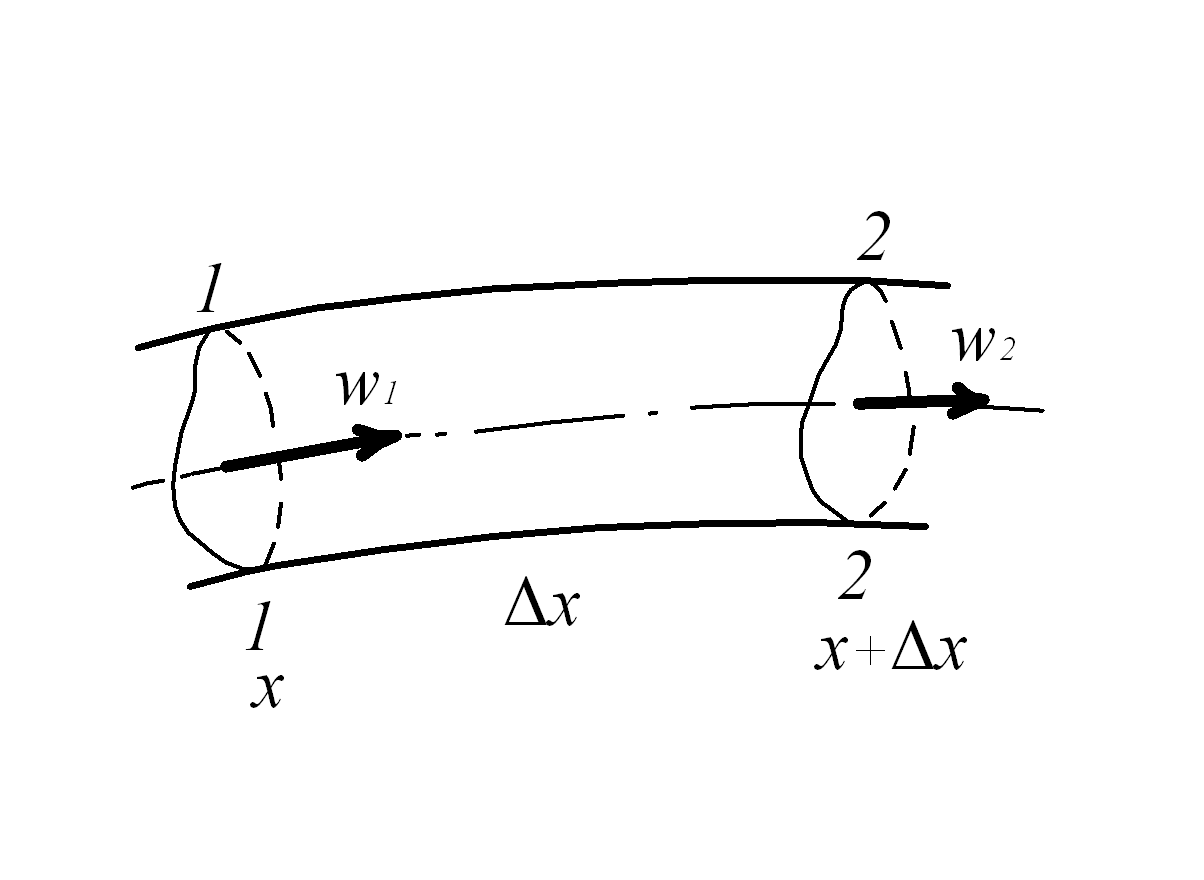 Рассмотрим отсек потока газа, ограниченный живыми сечениями 1-1 и2-2, отстоящими друг от друга на расстоянии
Рассмотрим отсек потока газа, ограниченный живыми сечениями 1-1 и2-2, отстоящими друг от друга на расстоянии  (рис. 2.1).
(рис. 2.1).
Рис.2.1. К выводу закона сохранения массы
Первое сечение характеризуется координатой  (
( - направление вдоль потока), второе – соответственно
- направление вдоль потока), второе – соответственно  .
.
Поскольку давление является функцией координаты  и газ - сжимаемая среда, то плотность
и газ - сжимаемая среда, то плотность  и скорость потока
и скорость потока  будут также функциями
будут также функциями  . В самом общем случае, когда движение неустановившееся величины
. В самом общем случае, когда движение неустановившееся величины  ,
,  ,
,  являются еще и функциями времени, т.е.
являются еще и функциями времени, т.е.

Переменным будет и массовый расход газа  . Причем, при неустановившемся течении в любой фиксированный момент времени
. Причем, при неустановившемся течении в любой фиксированный момент времени  массовые расходы газа в первом сечении
массовые расходы газа в первом сечении  и во втором сечении
и во втором сечении  определяются
определяются
 ;
;
 (2.1)
(2.1)
Согласно закону сохранения массы, разница  и
и  равна изменению массы газа, заключенной в отсеке потока длиной
равна изменению массы газа, заключенной в отсеке потока длиной  . Это изменение должно рассматриваться во времени, масса газа в рассматриваемом отсеке в любой фиксированный момент времени определяется как
. Это изменение должно рассматриваться во времени, масса газа в рассматриваемом отсеке в любой фиксированный момент времени определяется как  . Изменение этой массы во времени определяется как производная по времени
. Изменение этой массы во времени определяется как производная по времени  .
.
Следовательно, согласно закону сохранения массы, можно записать
 (2.2)
(2.2)
Разложим  в ряд Тейлора:
в ряд Тейлора:

Подставляя это разложение в (2.2) и учитывая, что  , будем иметь:
, будем иметь:

Поскольку длина отсека  не зависит от времени
не зависит от времени  , ее можно вынести из под знака производной. После сокращения на
, ее можно вынести из под знака производной. После сокращения на  последнее равенство можно записать:
последнее равенство можно записать:

Или, если учесть, что массовый расход можно выразить через среднюю скорость потока как произведение  ,
,
 (2.3)
(2.3)
Это уравнение называет уравнением неразрывности (или сплошности) для неустановившегося одномерного течения газа или любой сжимаемой среды.
В случае движения газа в трубах и каналах постоянного сечения  уравнение неразрывности (2.3) принимает вид
уравнение неразрывности (2.3) принимает вид
 (2.4)
(2.4)
В случае установившегося течения газа  и уравнение неразрывности (2.3) принимает вид
и уравнение неразрывности (2.3) принимает вид

Это равносильно тому, что вдоль потока (при установившемся движении) массовый расход не изменяется
 (2.5)
(2.5)
т.е. для любых двух сечений потока газа справедливо равенство:
 (2.5’)
(2.5’)
Соотношение (2.5) или (2.5') называют уравнением расхода.






