В практичних дослідженнях про тісноту кореляційної залежності судять по значенню вибіркового коефіцієнта кореляції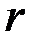 
. Оцінка 
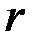величина випадкова. Нехай 
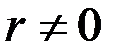. В цьому випадку перевіряється гіпотеза 
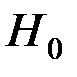про відсутність лінійного кореляційного зв’язку між змінними в генеральній сукупності. Якщо ця гіпотеза справедлива, то статистика 
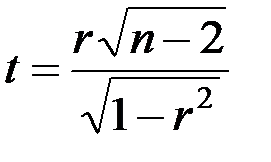має 
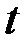- розподіл Стьюдента з 
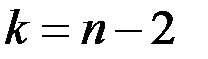степенями вільності. Гіпотеза 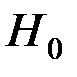відкидається, якщо 
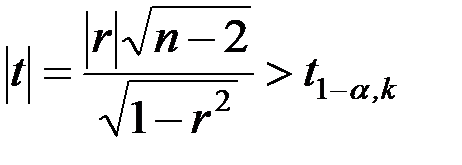, де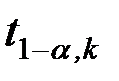 
- табличне значення 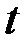- критерію Стьюдента, що визначається на рівні значущості 
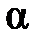при кількості степенів вільності .
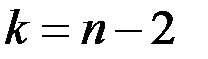◄Приклад 6.3 Перевірити на рівні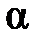 
=0,05 значущість коефіцієнта кореляції між змінними Х та Y за даними табл. 6.1.
Розв’язання. В прикладі 6.2 обчислено коефіцієнт кореляції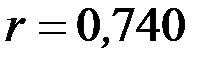 
. Статистика критерію 
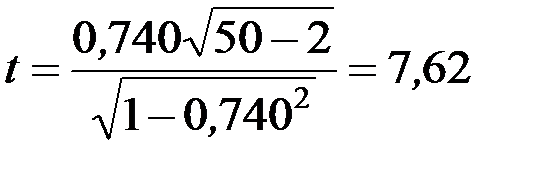. Для рівня значущості 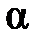=0,05 і кількості степенів вільності 
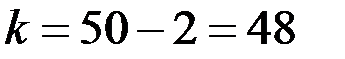знаходимо критичне значення статистики 
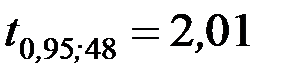. Оскільки 
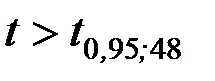, то коефіцієнт кореляції між добовим виробітком продукції Y і величиною основних виробничих фондів Х значно відмінний від нуля.►
Для значущого коефіцієнта кореляції 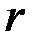доцільно знайти довірчий інтервал, який із заданою надійністю 
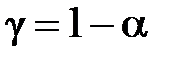накриває невідомий генеральний коефіцієнт кореляції 
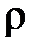. Для побудови такого інтервалу використовують спеціально підібрані функції від 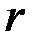, які збігаються до добре відомих розподілів. Найчастіше використовують 
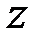- перетворення Фішера:
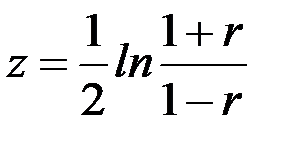(6.20) Розподіл 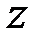вже при невеликих n є приблизно нормальним з математичним сподіванням 
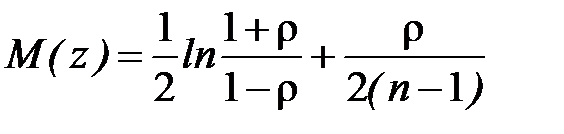і дисперсією 
.
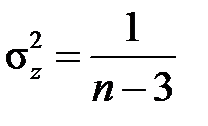Спочатку будується довірчий інтервал для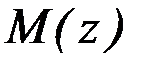 
:
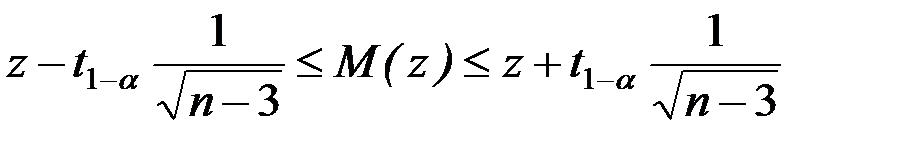, де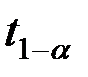 
- нормоване відхилення 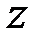, що визначається за допомогою функції Лапласа: 
.
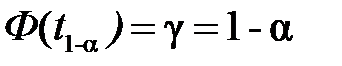Для визначення границь довірчого інтервалу для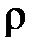 
існують спеціальні таблиці. За їх відсутності користуються формулою 
.
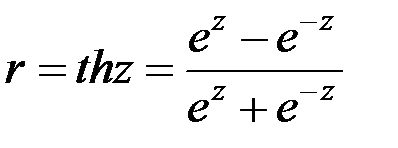Якщо коефіцієнт кореляції значущий, то коефіцієнти регресі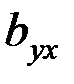ї 
і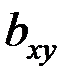 
також значно відрізняються від нуля, а інтервальні оцінки для відповідних генеральних коефіцієнтів регресі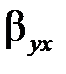ї 
і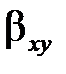 
можуть бути отримані за формулами, що спираються на те, що статистики 
, 
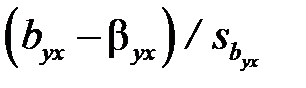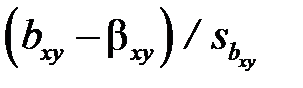мають t -розподіл Стьюдента з (n- 2) степенями вільності:
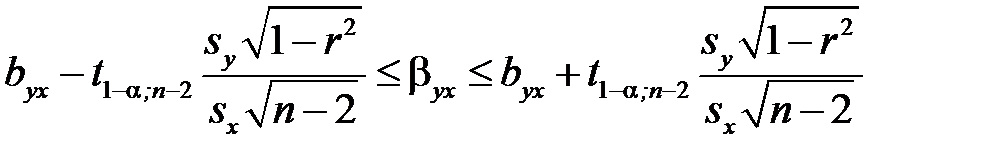(6.21)
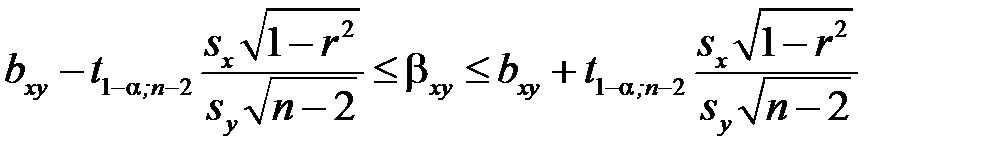(6.22)
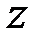- перетворення Фішера може бути застосовано при перевірці різних гіпотез відносно коефіцієнта кореляції. Наприклад, для перевірки значущості розбіжностей двох коефіцієнтів кореляці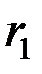ї 
і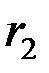 
, отриманих за вибірками об’ємів 
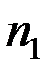і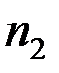 
для перевірки нульової гіпотези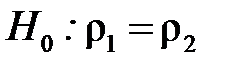 
застосовується статистика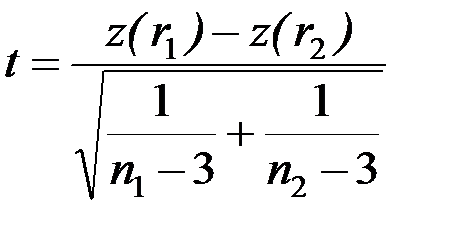 
(6.23)
Приклад 6.4 За даними таблиці 6.1 знайти з надійністю 0,95 інтервальні оцінки (довірчі інтервали) параметрів зв’язку між добовим виробітком продукції Y і величиною основних виробничих фондів X.
Розв’язання. Оскільки коефіцієнт кореляції X і Y значущий (див. приклад 6.3), то побудуємо довірчий інтервал для генерального коефіцієнта кореляції ρ, застосовуючи 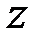- перетворення Фішера:
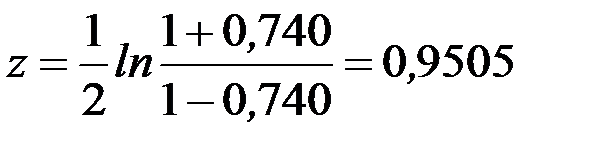. За таблицею функцій Лапласа і за умови 
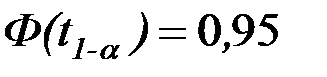, знаходимо 
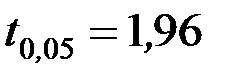. Побудуємо довірчий інтервал для M(z): 
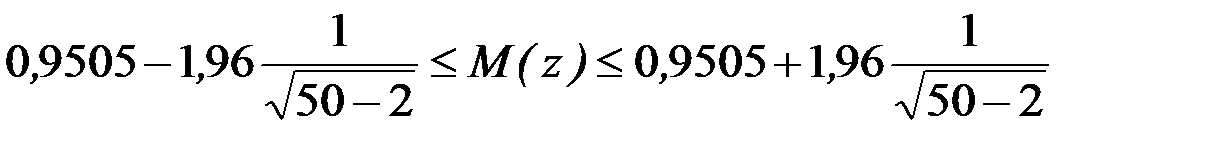, або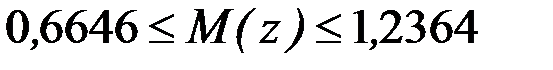 
. Знаходимо границі довірчого інтервалу для ρ, використовуючи спеціальну таблицю чи формулу: 
.
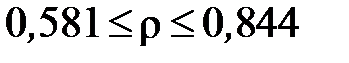Генеральний коефіцієнт кореляції ρ на рівні значущості 0,05 (з надійністю 0,95) накривається знайденим інтервалом.
Тепер побудуємо довірчі інтервали для генеральних коефіцієнтів регресі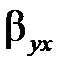ї 
і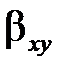 
. Спочатку визначимо середнє квадратичне відхилення змінних: 
; 
.
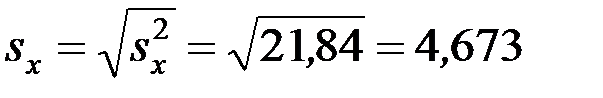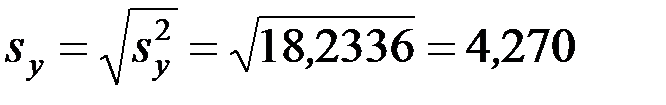Тепер за (6.21):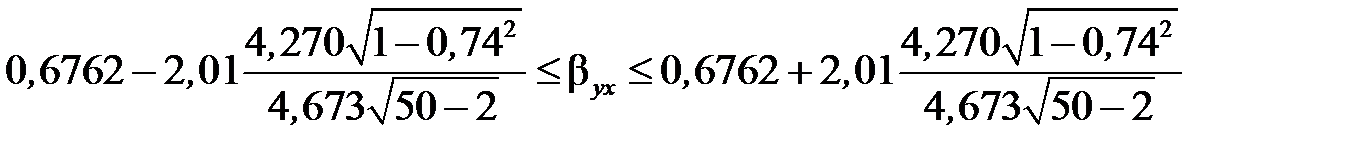 
.
Або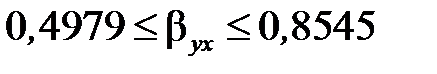 
.
Аналогічно за (6.22):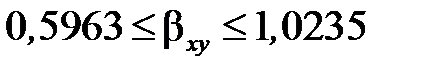 
►.
При змістовній інтерпретації параметрів ρ,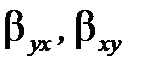 
слід врахувати в першу чергу їх інтервальні (а не тільки точкові) оцінки.
◄ Приклад 6.5 При дослідженні зв’язку між продуктивністю праці і рівнем механізації робіт на підприємствах однієї галузі промисловості, що розташовані в двох різних районах держави, обчислені коефіцієнти кореляці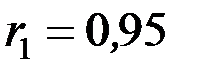ї 
і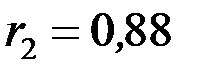 
за вибірками об’ємів відповідно 
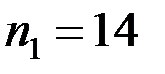і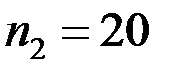 
. З’ясувати, чи є на рівні значущості 
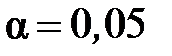суттєві розбіжності в тісноті зв’язку між змінними, що розглядаються на підприємствах галузі в цих районах.
Розв’язання. Гіпотеза, що перевіряється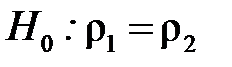 
. Альтернативна гіпотеза 
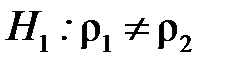. Статистика обчислюється за формулою (6.23):
. 
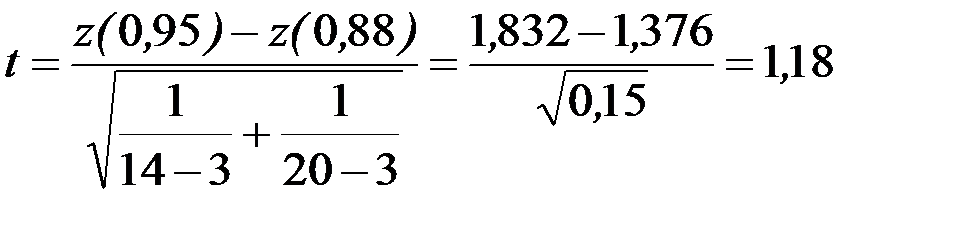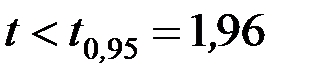. Отже, гіпотеза 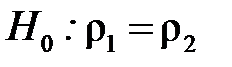не відкидається, тобто немає підстав вважати розбіжності суттєвими.►
