В хімічній технології для проведення масо- і теплообмінних процесів широке застосування знаходять насадочні колони різних конструкцій. Точність розрахунку режимних і конструктивних параметрів апаратів даного типу в значній мірі визначається достовірністю розрахунку коефіцієнтів масо- і тепловіддачі. Ці кінетичні характеристики залежать від режиму руху потоку, насадочних елементів і фізичних властивостей середовища. Через складність перебігу процесів знахождення коефіцієнтів масо- і тепловіддачі здійснюється, в основному, емпіричним шляхом. Для цього потрібно створення дорогих установок для проведення досліджень процесів переносу кожним типом насадочних елементів. В зв’язку з цим теоретичний шлях має переваги перед дослідним, оскільки він дозволяє скоротити термін і витрати на розрахунки масо- і теплообмінних процесів.
В межах єдиного підходу отримані рівняння, які дають можливість розрахувати коефіцієнти масо- і тепловіддачі в апаратах різних конструкцій, ґрунтуючись тільки на результатах дослідження контактних пристроїв. Математична модель процесів переносу в одно- чи двофазних середовищах залежить від гідродинамічних умов руху потоку і визначається характером затухання пульсації у в'язкому підшарку граничного шару.
Встановлено, що при SсТ 
РrТ 1 показник степеня функції залежить від співвідношень виду:
(60)
де аТ...DТ – коeфіцієнти турбулентного і а, D – молекулярного обміну теплом і масою, м2/с; ир – динамічна швидкість, м/с; δ1 – товщина в’язкого підшарку, м; α, β – відповідно коефіцієнти тепловіддачі (Вт/м2· 0С) і масовіддачі (м/с); y – поперечна координата граничного шару; SсТ = vТ/DТ, PrТ = vТ/аТ – турбулентне число Шмідта і Прандля.
Процеси масо- і тепловіддачі в газовій фазі як в сухих, так і в зрошувальних насадочних колонах характеризуються залежностями виду α~a2/3 і β~D2/3, що відповідає значенню показника степеня функції (60) n=3. В цьому випадку коефіцієнти масо- і тепловіддачі можна розраховувати за рівнянням:
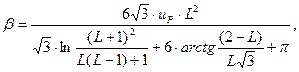(61)
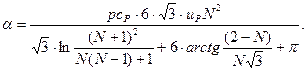(62)
де L = (R1Sc)-1/3; N = (R1Pr)-1/3; Sc, Pr – числа Шмідта і Прандля; R1= UP; δ1/v – безрозмірна товщина в’язкого підшару; v – коефіцієнт кінематичної в’язкості,м2/с; с – питома теплоємність, Дж/(кг·К); p – густина середовища, кг/м3.
Розглянемо варіанти застосування рівнянь (61) і (62) для визначення коефіцієнтів масо- і тепловіддачі під час руху газу в шарі насадочних елементів при відсутності зрошення рідиною. Для цього розробимо методи розрахунку основних параметрів моделі – ир і R1 .
Відомо, що турбулентний рух газу в насадці починається при ReГ>40, де ReГ=wК dЕ/(VВ. v) – число Рейнольдса; WК - швидкість газу в повному розрізі колони, м/с; dЕ – еквівалентний діаметр насадки, м; VВ – питомий вільний об’єм.
Відповідно до двошарової моделі турбулентного граничного шару Прандля, параметр R1 11,6 є істинним для плоского граничного шару без завихрення. Оскільки граничний шар на поверхні насадочних елементів характеризується кривизною поверхні і градієнтом тиску, R1 може відрізнятися від значення даного параметру на пластині.
Для визначення безрозмірної товщини в’язкого підшарку в граничному шарі з різними завихреннями покажемо опір переносу імпульсу у вигляді:
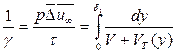, (63)
де 
– коефіцієнт переносу імпульсу, м/с;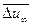 
– середня рушійна сила переносу імпульсу, м/с; τ – дотична напруга, Па.
При SсТ РrТ 1 залежність для коефіцієнта турбулентної в’язкості vТ(y) приймемо в формі (60). Тоді з виразу (63) отримаємо середнє значення:
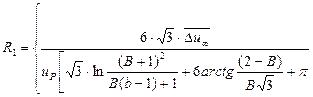, (64)
де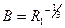 
.
Динамічну швидкість в рівняннях (61), (62) та (64) знайдемо на основі формули: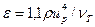 
де ε – дисипація енергії турбулентного потоку, Вт/м3. Підставляючи в дане співвідношення середнє значення коефіцієнта (60), отримаємо:
, (65)
де середнє значення дисипаційної енергії стабілізованого газового потоку в вільному об’ємі насадочної колони:
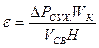, (66)
де Н – висота шару насадки, м; ∆РСУХ. – перепад тиску для сухої насадки, що знаходиться за рівнянням:
(67)
Для коефіцієнту гідравлічного тиску ξГ використовують емпіричні вирази.
В шарі насадочних елементів швидкість газового потоку через звуження і розширення прохідного перерізу каналів є непостійна. Вона змінюється в межах від середньої швидкості в вільному перерізі колони до максимального значення в самому вузькому прохідному перерізі. Враховуючи, що на поверхні сухих насадочних елементів швидкість газу рівна нулю, тоді середня рушійна сила переносу імпульсу у виразі (64) буде визначатися середньою швидкістю на зовнішній границі граничного шару і вздовж осі потоку:
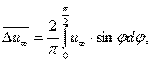(68)
де при 
=00 u∞≈WК , а при u∞≈Wмах.
Максимальну швидкість газу вздовж каналу знайдемо з рівняння:
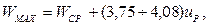(69)
де WCР. – середня швидкість газу в перерізі каналу, м/с.
В результаті зазначеного перетворення з виразу (68) та (69) отримаємо:
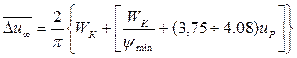, (70)
де відносний мінімальний прохідний переріз в шарі насадки:
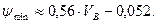
Рівняння (61) з параметрами (64) і (65) було перевірене шляхом розрахунку коефіцієнта масовіддачі в сухій насадці з кілець Рашига, виготовлених з нафталіну (рис. 50). Коефіцієнт тепловіддачі (62) був розрахований для колони, заповненої металевими циліндрами і капроновими паралелепіпедами під час руху нагрітого повітря (рис. 51). Кореляція з дослідними даними знаходиться в межах похибки експерименту.
Основні параметри математичної моделі були знайдені при розв’язуванні системи рівнянь (64) і (65). Для виключення ітераційних циклів були виконані перетворення рівнянь (61) і (62).
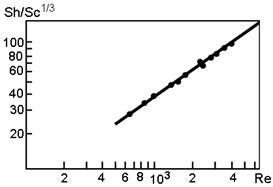
Рис. 50. Залежність комплексу Sh/Sc1/3 від числа Рейнольдса при випаровуванні нафталіну з поверхні пористих тіл в насадочній колоні, що отримана в результаті розрахунку за рівнянням (61) і за експериментальними даними
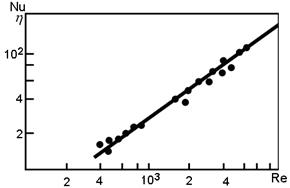
Рис. 51. Залежність числа Нуссельта від числа Рейнольдса
під час руху нагрітого повітря на насадочній колоні, що отримана в результаті розрахунку за рівнянням (62) і за експериментальними даними
Підставивши в рівняння (61) динамічну швидкість (65), отримаємо:
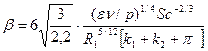, (71)
де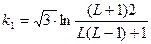 
, 
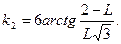
Знаменник виразу (71) b=R1 5/12[k1+k2+π] є функцією b=f(R1,Sc). В результаті розрахунків для насадочних колон різноманітних конструкцій встановлено, що її значення несуттєво залежить від параметрів R1 i Sc і складає b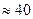 
при ReГ = 102-104 i Sc = 0,5-3. Тоді рівняння (71) отримає вигляд:
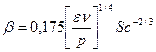. (72)
Аналогічно запишемо:
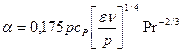. (73)
Результати розрахунку чисел Шервуда Sh=βdE/D і Нуссельта Nu = αdЕ/(apcP), які отримані з співвідношень (72) і (73), наведені в таблицях 13 та 14.
Таблиця 13
Результати розрахунку числа Шервуда в колоні з кільцями Рашига
| № з/п | Rer | Sh/Sc-1/3 за рівнянням (72) | Sh/Sc-1/3 за рівнянням Гільден-блата | Розходження за рівнянням (72), % | Sh/Sc-1/3 за рівнянням Аерова | Розходження за рівнянням (72), % |
| 7,39 | 8,31 | -11,0 | 7,47 | -1,0 | ||
| 14,04 | 15,14 | -7,0 | 13,35 | 5,0 | ||
| 22,81 | 23,84 | -4,0 | 20,81 | 9,0 | ||
| 37,05 | 37,54 | -2,0 | 32,43 | 14,0 | ||
| 70,36 | 68,43 | 3,0 | до 2.103 | |||
| 114,31 | 107,75 | 6,0 | - | - | ||
| 185,70 | 169,67 | 9,0 | - | - |
В насадочній колоні, яка зрошується, вільний об’єм зменшується на величину затримки рідини vР. На поверхні розділу фаз в результаті тертя газу і рідини виникають дотичні напруги. Це приводить до збільшення гідравлічного опору порівняно з сухою насадкою при однаковій швидкості газу WК. Дисипація енергії в цьому випадку буде складатись з суми енергії, дисипуючої в об’ємі змоченою рідиною εA-D насадки, і енергії, дисипуючої в результаті тертя і опору незмоченої насадки.
Таблиця 14
Результати розрахунку числа Нуссельта в колоні з металевими циліндрами з капроновими гранулами
| № з/п | Rer | Nu/Pr-1/3 за рівнянням (73) | Nu/Pr-1/3 за формулою роботи | Розход- ження, % |
| 10,37 | 9,95 | 4,0 | ||
| 19,47 | 18,91 | 3,0 | ||
| 31,36 | 30,71 | 2,0 | ||
| 58,88 | 58,33 | 1,0 | ||
| 94,83 | 94,77 | - | ||
| 119,51 | 119,9 | -1,0 |
Для розрахунку коефіцієнту масовіддачі (61) в газовій фазі зрошувальної колони необхідно визначити параметри граничного шару uР і R1 на міжфазній поверхні „газ-рідина”.
Динамічну швидкість знайдемо за рівнянням (65) зі значенням дисипуючої енергії:
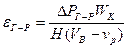, (74)
де vР – затримка рідини в насадці, м3/м3; ∆РГ-Р – складова перепаду тиску в зрошувальній насадці ∆РЗР ., яка обумовлена рідиною, що стікає, Па.
Якщо вся поверхня насадочних елементів зволожена рідиною, то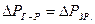 
. У випадку коефіцієнта поверхні ψW<1, що має місце при плівковому режимі роботи, запишемо:
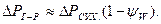
Середня рушійна сила переносу імпульсу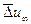 
в формулі (64) буде мати більше значення, ніж в сухій насадці внаслідок звуження каналів рідиною, яка стікає. Крім цього, неообхідно враховувати швидкість рідкої фази у вигляді 
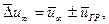де 
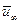– середня швидкість газу вздовж осі потоку, м/с; 
– середня швидкість руху рідини на поверхні розділу.
Розрахунки коефіцієнта масовіддачі (71) в газовій фазі при плівковому режимі роботи насадочних колон показують, що функція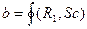 
знаходиться в межах b = 30-90. Тоді при збільшенні витрати рідини значення параметрів b зростає, що пов’язане зі збільшенням швидкості газу за рахунок зменшення прохідного перерізу каналів. Результати розрахунку добре апроксимуються залежністю b=538,9q0,4, де q – питома витрата рідини, м3/(м2·с). Тоді середній коефіцієнт масовіддачі (71) можна представити у вигляді:
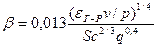. (75)
Звідси об’ємний коефіцієнт масовіддачі:
, (76)
де aV – питома поверхня насадки, м2/м3; ψА – коефіцієнт активної поверхні масопередачі.
Результати розрахунку об’ємного коефіцієнта масовіддачі (76) представлені на рис. 52. Було проведене порівняння з емпіричною залежністю:
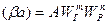, (77)
де WГ, WР – питома витрата газу і рідини, кг/(м2·год). Витрата рідини в колоні складає 10 м3/(м2·год).
Були отримані дослідні коефіцієнти масовіддачі, віднесені до змоченої поверхні насадки. Оскільки в більшості випадків ψW>ψA, тоді для порівняння з експериментальними даними запишемо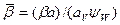 
, де: 
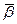– коефіцієнт масовіддачі, віднесений до змоченої поверхні насадки, м/с. Результати розрахунку числа Шервуда 
для сідел Берля наведені на рис. 53, де: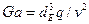 
– число Галілея.
Рівняння (76) було перевірене при плівковому режимі роботи колони з кільцями Рашига і сідлами Берля з номінальними розмірами 15-35 мм, ReГ = (2-20) · 102 і q = (2,0-9,0) · 10-3. Кореляція з емпіричними результатами знаходиться в межах похибки експериментальних досліджень.
R 103, 1/4
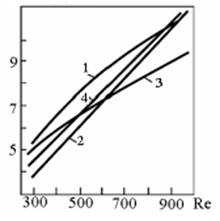
Рис. 52. Результати розрахунку об’ємного коефіцієнта
масовіддачі в насадочній колоні з кільцями Рашига діаметром 25 мм при абсорбції амоніаку водою, які отримані за емпіричними виразами Дотерті (крива 1), Двайра і Доджі (крива 2), Бордена (крива 3), а також за рівнянням (76) (крива 4)
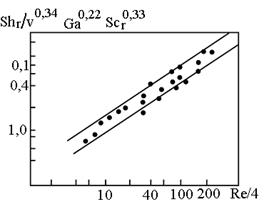
Рис. 53. Залежність числа Шервурда від числа Рейнольдса, яка отримана в результаті розрахунку за рівнянням (76) і за експериментальними даними
Розроблену математичну модель можна рекомендувати для розрахунку коефіцієнтів масо- і тепловіддачі в сухих і зрошувальних насадочних колонах, використовуючи тільки результати гідравлічного дослідження.
