Задача на нахождение точки пересечения прямой линии с плоскостью является основной позиционной задачей начертательной геометрии. Она входит составной частью в решение многих задач в различных разделах курса. От того, насколько хорошо она будет освоена, зависит успешное изучение последующего материала. В общем виде решение этой задачи состоит из трех последовательно выполняемых операций:
- через данную прямую проводим вспомогательную проецирующую плоскость;
- строим линию пересечения данной плоскости и вспомогательной;
- определяем точку пересечения данной прямой с построенной линией пересечения плоскостей.
На рис.33 показано решение задачи на ортогональном эпюре.
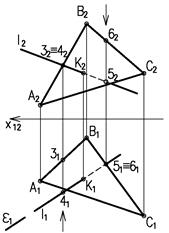Дана прямая ℓ и плоскость ά (АВС). Через прямую проведена горизонтально-проецирующая плоскость ε. Горизонтальный след плоскости ε1 совпадает с горизонтальной проекцией прямой ℓ. Построена прямая 1-2 линия пересечения данной плоскости ά и вспомогательной плоскости ε. Сначала отмечены горизонтальные проекции точек 11 и 21 затем по линиям проекционной связи фронтальные проекции 12 и 22. Отмечена точка К2 фронтальная проекция точки пересечения данной прямой с построенной прямой 1-2, и по линии проекционной связи найдена ее горизонтальная проекция К1.
Решение задачи должно завершиться определением видимых и невидимых участков на проекциях данной прямой. Для этого на фронтальной проекции на прямых АВ и ℓ возьмем конкурирующие точки 3 и 4 (рис. 34) на фронтальной проекции точка 4 закрывает точку 3, так как у нее координата Y больше (см. на горизонтальную проекцию этих точек), поэтому прямая ℓ видимая до точки пересечения с плоскостью треугольника АВС (т. К2). Для установления видимости на горизонтальной проекции возьмем конкурирующие точки 5 и 6 на прямых ℓ и ВС. Координата Z точки 5 меньше координаты Z точки 6 (см. фронтальные проекции этих точек), следовательно точка 5 ниже точки 6, а это значит что прямая ℓ невидимая до точки пересечения с плоскостью треугольника АВС (т. К1).
Следует отметить частный случай решения задачи на пересечение прямой с плоскостью, когда прямая занимает проецирующее положение. В этом случае одна из проекций искомой точки оказывается известной, остается определить положение второй проекции.
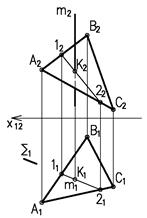
На рис.35, прямая m в горизонтально-проецирующем положении. Горизонтальная проекция К1 точки ее пересечения с плоскостью тоже известна – она находится в той точке, в которую проецируется вся прямая. Для определения фронтальной проекции искомой точки проводим произвольную плоскость ∑1. Находим линию 1-2 пересечения плоскости ∑ и плоскости АВС, а затем находим фронтальную проекцию точки А2.
Задача. Построить линию пересечения 2-х плоскостей ά (∆ АВС) и β (m//n) (рис 36).
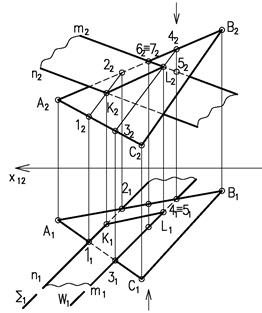
Решение задачи сводится к нахождению точек пересечения прямой n с плоскостью ά и прямой m с плоскостью ά.
