Взаимное положение прямых

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для самостоятельной работы по курсу

«Начертательная геометрия» к разделу «Точка, прямая и плоскость»

 

 

Макеевка 2010

УДК 515

 

Методические указания для самостоятельной работы по курсу «Начертательная геометрия» к разделу «Точка, прямая и плоскость» (для студентов I курса всех специальностей) / Сост. И.Г. Балюба, А.А. Крысько, З.А. Наминас – Макеевка: ДонНАСА, 2010. – 38 с.

 

 

Помогут самостоятельно освоить курс начертательной геометрии под руководством и контролем преподавателя. Содержат рекомендации по изучению теоретического материала со ссылками на основные учебники. Даны варианты для самостоятельного выполнения графических работ и их образцы и рекомендации к выполнению.

 

Составители И.Г. Балюба, проф.

А.А. Крысько

З.А. Наминас

 

Ответственный

за выпуск С.Г. Кузнецов, проф.

 

МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ УКРАИНЫ

 

ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ

СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ

 

КАФЕДРА «ГРАДОСТРОИТЕЛЬСТВО И ИНЖЕНЕРНАЯ ГРАФИКА»

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для самостоятельной работы по курсу

«Начертательная геометрия» к разделу «Точка, прямая и плоскость»

(для студентов I курса всех специальностей)

№ кода 0701

У т в е р ж д е н о

на заседании кафедры

«Градостроительство и

инженерная графика».

Протокол № 4 от 26.11.2010

 

 

Макеевка 2011

Содержание

Точка

Прямая линия

Взаимное положение прямых.

Графическая работа Эпюр 1 (лист 1).

Плоскость

Параллельность прямой и плоскости. Параллельность двух плоскостей

Графическая работа Эпюр1(лист 2).

Пересечение двух плоскостей

Пересечение прямой линии с плоскостью.

Прямая, перпендикулярная плоскости

Взаимно перпендикулярные плоскости

Графическая работа Эпюр1(лист 3).

Список литературы.

Точка

 

Построение изображений предметов в начертательной геометрии основано на методе проецирования. Так как каждый предмет можно рассматривать как совокупность точек, покажем сущность метода проецирования на примере одной точки. Проведем через точку А пространства (рис.1) прямую линию и отметим точку А¹ пересечения этой линии с плоскостью П₁, на которой будем строить изображение предмета.

Точка А называется оригиналом, точка А¹ проекцией, прямая АА¹ – проецирующим лучом, плоскость П₁ – плоскостью проекций. Если проецирующий луч АА¹ перпендикулярен плоскости проекций П₁, то проецирование называется ортогональным, а точка А¹ называется ортогональной проекцией точки А.

Спроецировав по этому принципу все точки предмета, получим его изображение.

На рис.1 видно, что одна проекция точки не определяет ее положения в пространстве, так как в точку А¹ проецируются все точки проецирующего луча АА¹. Для того чтобы по чертежу можно было определить положение точки в пространстве необходима ещё одна проекция на другую плоскость проекций.

Возьмем две взаимно перпендикулярные плоскости проекций П₁ и П₂ (рис.2).

Плоскость П₁ называется горизонтальной плоскостью проекции, а плоскость П₂ – фронтальной плоскостью проекций. Линия их пересечения называется осью проекций и обозначается Х₁₂. Спроецируем точку А ортогонально на обе эти плоскости (проецирующие лучи АА₁ и АА₂ перпендикулярны соответствующим плоскостям П₁ и П₂). Получим две проекции точки А₁ и А₂.

Точка А₁ называется горизонтальной проекцией точки А, а точка А₂ - фронтальной проекцией.

В трехмерном пространстве положение точки определяется тремя прямоугольными (декартовыми) координатами. Отметим на оси Х₁₂ точку О – начало координат. Координатную ось Х совместим с осью проекций Х₁₂, координатную ось Y – с плоскостью П₁, а Z – с плоскостью П₂. Тогда отрезок ОА_х определит координату Х точки А, отрезок А_хА₁ – координату У, а отрезок А_хА₂ – координату Z. Таким образом, две проекции точки А₁ и А₂ полностью определяют ее положение в пространстве.

Координатные оси Y и Z определяют третью плоскость проекций, перпендикулярную плоскостям П₁ и П₂. Эта плоскость называется профильной плоскостью проекций и обозначается П₃. Положительные значения координат указаны на рис.2 стрелками.

Повернем плоскость П₁ вокруг оси Х₁₂ до совмещения с плоскостью П₂.

Получим плоский чертеж, называемый эпюром (рис.3). Фронтальная и горизонтальная проекции точки располагаются на одной прямой, перпендикулярной оси Х₁₂. Эта линия называется линией проекционной связи. Положение фронтальной проекции точки А₂ определяют координаты Х и Z, горизонтальной проекции А₁ – Х и Y.

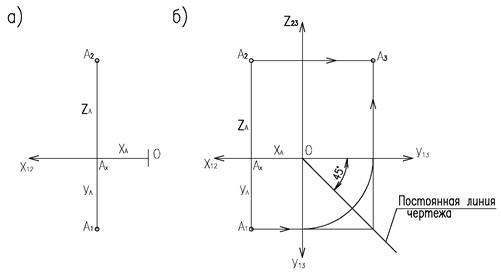
На рис.3б показано как построить профильную проекцию точки А₃ по горизонтальной и фронтальной проекциям.

Плоскости П₁ и П₂ делят все пространство на четыре четверти, отмеченные на рис.4 римскими цифрами I, II, III и IV. Точка А находится в I четверти. Все ее координаты имеют положительное значение. У точки В, находящейся во II четверти, координата Y будет отрицательной, у точки С в III четверти отрицательными будут координаты Y и Z, а у точки D в IV четверти – координата Z. При совмещении плоскостей проекций обе проекции точки В окажутся выше оси Х₁₂, точки D ниже оси Х₁₂, а у точки С горизонтальная проекция выше оси Х₁₂, а фронтальная ниже. Координаты точки показывают величины расстояний точки от плоскости проекций. Координаты Y – это расстояние точки от плоскости проекций П₂, координата Z – от плоскости проекций П₁, координата Х – от плоскости проекций П₃. Если точка лежит на одной из плоскостей проекций, то одна из ее координат будет равна нулю.

 

Прямая линия

Положение прямой линии в пространстве определяется двумя ее точками. Чтобы построить проекции прямой, возьмем на ней две произвольные точки А и В (рис.5) и спроецируем их на плоскости проекций П₁ и П₂. Соединяя прямыми одноименные проекции этих точек, получим проекции прямой.

 

Две проекции прямой полностью определяют ее положение в пространстве.

Если точка С лежит на прямой, то ее проекции лежат на соответствующих проекциях прямой. Если эта точка делит отрезок АВ в каком либо отношении, то в том же отношении проекции точки делят проекции отрезка.

Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.

Ортогональные проекции отрезка прямой общего положения всегда меньше длины самого отрезка. Длину отрезка прямой можно определить по двум его проекциям.

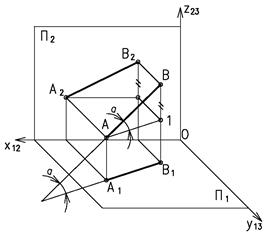Рассмотрим прямоугольный треугольник АВ1 (рис.6).

Катет А1 равен горизонтальной проекции отрезка А₁В₁, а катет В1 – разности координат его концов, взятой на другой проекции отрезка. Гипотенуза этого треугольника равна длине отрезка или, как иногда говорят, его натуральной величине.

Угол между натуральной величиной отрезка и его проекцией определяет угол наклона прямой к соответствующей плоскости проекций.

На рис. 7а натуральная величина (н.в.) отрезка определена на горизонтальной плоскости проекций и угол ά есть угол наклона прямой АВ к горизонтальной плоскости проекций П₁.

 

Аналогично на рис.7б натуральная величина определена на фронтальной плоскости проекций. В этом случае угол β определяет угол наклона прямой к фронтальной плоскости проекций П₂. Этот способ определения натуральной величины отрезка прямой называется способом прямоугольного треугольника.

Следами прямой АB называются точки пересечения ее с плоскостями проекций (рис.8). Точка Н – горизонтальный след прямой АВ. Точка F – фронтальный след прямой АВ.

Для определения на эпюре горизонтального следа прямой (рис.9) необходимо продолжить фронтальную проекцию прямой до пересечения с осью Х₁₂ и отметить точку Н₂. Из этой точки провести линию проекционной связи до пересечения с горизонтальной проекцией прямой. Получим точку Н₁. Точки Н₁ и Н₂ определяют горизонтальный след прямой. Аналогично определяется фронтальный след прямой F (F₁, F₂).

 

Прямые, параллельные или перпендикулярные плоскостям проекций, называются прямыми частного положения. Прямые, параллельные плоскостям проекций называются линиями уровня.

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной и обозначается буквой h (h_1, h₂) (рис.10,а). На горизонтальную плоскость проекций она проецируется в натуральную величину и может быть расположена под разными углами к оси Х₁₂ в зависимости от положения в пространстве, а фронтальная ее проекция всегда параллельна оси Х₁₂.

Аналогично прямая, параллельная фронтальной плоскости проекций П₂, считается фронтальной и обозначается буквой f (f_1,f₂) (рис.10,б). Горизонтальная проекция фронтали всегда параллельна оси Х₁₂.

Прямая, параллельная профильной плоскости проекций называется профильной прямой (рис.10 в). У профильной прямой горизонтальная и фронтальная проекции перпендикулярны оси Х₁₂.

 

Прямые, перпендикулярные плоскостям проекций, называются проецирующими.

Прямая, перпендикулярная горизонтальной плоскости проекций, – горизонтально-проецирующая (рис.11а). На горизонтальной плоскости проекций П₁ она проецируется в точку, а фронтальная ее проекция перпендикулярна оси Х₁₂.

 

Аналогично, прямая перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая (рис.11б), а прямая перпендикулярная профильной плоскости проекций П₃ – профильно-проецирующая (рис.11,в).

 

Взаимное положение прямых.

 

Две прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися.

Если в пространстве две прямые параллельны, то их одноименные проекции также параллельны (рис.12). Параллельность профильных прямых не всегда очевидна. Хотя их горизонтальные и фронтальные проекции параллельны, сами прямые могут быть не параллельны. Для определения их взаимного положения можно построить профильную проекцию (рис.12б).

 

 

Пересекающиеся прямые – это прямые имеющие общую точку, следовательно, если прямые в пространстве пересекаются, то точки пересечения их одноименных проекций лежат на одной линии проекционной связи (рис.13).

Скрещивающиеся прямые не имеют общей точки, поэтому точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рис.14). Точкам пересечения одноименных проекций скрещивающихся прямых соответствуют в пространстве две точки, расположенные на разных прямых.

Пары точек, у которых какие-либо одноименные проекции совпали, называются конкурирующими (одна из них «закрывает» другую). Из двух конкурирующих точек видна та, у которой больше одна из координат (две другие совпадают). Например, координата Z (рис.14) у точки М больше, чем у точки N, следовательно, прямая а в этом месте расположена выше прямой в и будет видима при взгляде сверху, т.е. на горизонтальной проекции. Аналогично, у точки L координата Y больше, чем у точки К, следовательно, в этом месте прямая а расположена ближе к зрителю и будет видима на фронтальной проекции. Определение видимости конкурирующих точек позволит нам в дальнейшем определять видимость прямой относительно плоскости.

Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций(рис 15).

 

 

Исключением является тот случай, когда угол между прямыми равен 90° (прямой угол). Чтобы этот угол проецировался без искажений на одну из плоскостей проекций, достаточно чтобы одна сторона угла была параллельна этой плоскости проекций (рис.16).