В основе определения лежит интеграл
 ,
,
в котором u1,1' (t) – непрерывная функция времени, δ(t)- дельта-функция, выступающая как импульсная характеристика, m – целое число точек, на которых задаётся процесс дискретизации. Интеграл не может быть равным сумме. Эта запись имеет право на существование как отражение процесса дискретизации.
Собственно, процедура превращения непрерывной функции в дискретную по времени заключена не в математической сущности интегрирования на основе δ(t)- функции, поскольку каждый раз рассматривается одна точка с бесконечно малой окрестностью, а на основе принятия сущности соответствующей дискретному множеству точек для выборки.
Как следует из определения этой функции, процесс интегрирования заключается в применении теоремы о среднем на бесконечно малой области, которой принадлежит точка, в которой δ(t) = ∞.
Таким образом, проводится дискретизация оси времени t точками, в которых задаётся δ(t). Расстояние между этими точками принимается равным некоторому интервалу Т.
Для каждой точки «m» интегрирование определяется формулой
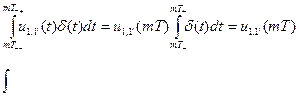 .
.
Совокупность таких значений можно записать в виде суммы по количеству точек, как это сделано в исходной формуле.
В литературе принято всю представленную процедуру заменить операторным представлением
u1,1'(t)δ(t) = U1,1',
где U1,1' – мгновенное значение функции u1,1'(t) в момент времени t, δ(t) – интерпретирована единичным импульсом.
Формула показывает результат: запись
u1,1'(t)δ(t)
означает мгновенное значение U1,1', соответствующее моменту времени t.
Полученное выражение дискретной функции времени можно использовать для получения соответствующего преобразования Лапласа от δ(t) - дискретизированной функции времени.
Следует здесь отметить, что преобразование Лапласа от последовательности прямоугольных импульсов разной амплитуды расходится и лишь δ(t) - последовательность даёт возможность получить указанное преобразование.

Если провести преобразование – внести интеграл под знак суммы и провести интегрирование в области точки «m» с учётом δ(t) функции, можно получить выражение

Если ряд сходится, то полученная формула представляет непрерывную функцию от комплексной частоты «p».
Положим z = epT.
Тогда полученное выражение перепишем с обозначением результата в виде функции от z.

Это выражение, при условии, что ряд сходится, носит название Z - преобразования из временной области в частотную (область комплексных частот). Особенность этого вида преобразования по отношению к известным – Фурье и Лапласу – заключается в том, что это частотное преобразование дискретной во временной области функции. Однако, если рассматривать зависимость модуля и аргумента функции U1,1'(z) от частоты, то они представляют собой непрерывные функции по частоте.
Рассмотрим несколько примеров.
Пусть рассматривается аналог единичной функции в дискретной области
1(mT). Z – преобразование запишется в виде

Сумму можно представить в виде
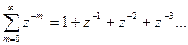
Если |z|>1, то данный ряд сходится, и сумма ряда определяется по формуле
 .
.
Проверим, выполняется ли принятое предположение для z = epT, если принять p = jω.
В этом случае z = CosωТ + jSinωТ и модуль z равен 1. Предположение не выполняется, однако если принять в качестве p полное выражение комплексной частоты p = σ + jω, то принятое предположение относительно модуля z будет выполняться.
В дальнейшем будем полагать под z именно такое условие.
Таким образом, преобразование

от дискретной единичной функции времени есть дробно – рациональное выражение в z области.
Рассмотрим другую, скажем, экспоненциальную функцию.
Пусть дискретная функция задана формулой
♥ u1,1'(mT) =exp(αmT), t>0.
Соответствующее Z-преобразование имеет вид
♪ U1,1'(z) = 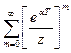 .
.
В этом выражении отношение, заданное в скобках также можно рассматривать как геометрическую прогрессию. Следовательно, если |exp(αT)/z|<1, то ряд сходится и сумма имеет вид


Рассмотрим линейную функцию
U1,1'(z) =  .
.
Приём, который здесь применён, может быть использован и в других случаях, например для степенных функций от tк:
 .
.
Здесь возможно представление примера, в котором можно построить графики некоторой дискретной по временной оси функции и её представление в Z- форме, также используя по временной оси дискретное множество точек. Это распределение целых чисел, начиная с нуля. На каждой точке восстановим столбик высотой соответствующей амплитуды у Z в степени равной (-к).






