Из формул j = evn и j = eE (см. Постоянный ток) получается выражение для проводимости s:

| Зависимость проводимости от заряда e носителя тока, концентрации n носителей и u = v/Е – подвижности носителей (по смыслу подвижность – это скорость дрейфа в расчете на единицу напряженности приложенного электрического поля.) |
Зависимость проводимости от температуры определяется главным образом зависимостью от температуры концентрации n носителей, подвижность u слабо зависит от температуры. Для полупроводников хвост распределения Ферми-Дирака (см. ранее) попадает в зону проводимости, поэтому для них может быть использовано классическое МБ распределение. Если принять, что в распределении ФД  , концентрацию носителей можно записать в виде:
, концентрацию носителей можно записать в виде:
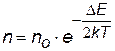 * *
| концентрация носителей в зоне проводимости полупроводникав зависимости от температуры; DЕ - ширина запрещенной зоны |
В собственном полупроводнике носителями тока являются электроны и дырки, поэтому для проводимости можно записать:
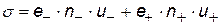
| проводимость полупроводника (электронная и дырочная) | 
|
Концентрация электронов и дырок одинакова. приближенно можно считать, что и их подвижность одинакова, тогда с учетом (*), получим:

| Зависимость проводимости собственного полупроводника от температуры В константу sо включены все величины, не зависящие от температуры. | 
|

| Логарифмируя, получим уравнение прямой линии, по наклону которой можно определить ширину запрещенной зоны. [xxv] |
Собственные полупроводники широко применяются в технике. Сильная зависимость сопротивления от температуры позволяет использовать их в качестве очень чувствительных термометров, а также для контроля силы тока в цепи.
В этом случае их называют термисторами или терморезисторами. Например, германиевый термистор применяется для измерения очень низких температур. Зависимость сопротивления от давления используется в тензодатчиках.
Примесные полупроводники. Рассмотрим качественно зависимость проводимости примесных полупроводников от температуры. На рис. приведен типичный график зависимости lns от обратной абсолютной температуры. Он характерен как для полупроводников n – типа, так и для р – типа. То, что кривая представляет собой прямые отрезки в таких координатах, показывает, что проводимость зависит от температуры экспоненциально.

|
Удобнее рассматривать график для полупроводника n – типа (зонную схему – см. ранее). При небольших температурах (отрезок ab) проводимость растет за счет перехода электронов с донорных уровней в зону проводимости. Начиная с некоторых температур проводимость оказывается независящей от температуры (участок bc). Это объясняется тем, что все электроны из донорной зоны перешли в зону проводимости. При дальнейшем нагревании проводимость начинает резко увеличиваться за счет переброски электронов из валентной зоны (участок cd). По наклону прямой ab можно найти ширину запрещенной зоны DЕ1, а по наклону прямой cd ширину запрещенной зоны DЕ2 .






