Пример П4.1
Найдите реакцию u 2(t)на выходе цепи, схема которой представлена на рис. П4.1, если на ее вход подано периодическое колебание, заданное в виде усеченного ряда Фурье: u 1(t) = 6 + 10cos 105 t + 5cos (2×105 t + 60°) В. Значения параметров элементов цепи: R 1 = R 2 = 200 Ом, L = 1мГн. Постройте спектры амплитуд входного и выходного колебаний.
Рис. П4.1
Решение
Найдем прежде всего комплексную передаточную функцию 
, для чего подадим на вход цепи гармоническое напряжение u 1(t) = Um 1cos (w t + j1), тогда комплексная амплитуда реакции цепи:
,
а передаточную функцию найдем, поделив 
на комплексную амплитуду воздействия:
.
Модуль комплексной передаточной функции определяет амплитудно-частотную характеристику цепи
,
а ее аргумент, равный разности аргументов числителя и знаменателя, – фазочастотную характеристику цепи
.
По данным примера R 1 = R 2 = 200 Ом, L = 10–3 Гн, тогда
;
.
Вычислим значения АЧХ и ФЧХ на частотах гармонических составляющих входного колебания w = 0,w1 = 105 с–1, w2 = 2w1 = 2×105 с–1.
При w = 0: ½ H (j w)½ = 1; q(w) = 0.
При w1 = 105 с–1: 
;
.
При w2 = 2×105 с–1: 
;
.
Комплексная амплитуда k -й гармоники выходного колебания
Таким образом, амплитуда k -й гармоники изменяется в | H (jk w1)| раз, а начальная фаза – на величину q(k w1).
В соответствии с этим напряжение на выходе цепи
u 2(t) = 6 + 10×0,79cos(105 t – 18,4°) + 5×0,63cos(2×105 t + 60° – 18,4°) =
= 6 + 7,9cos(105 t – 18,4°) + 3,15cos(2×105 t + 41,6°).
На рис. П4.2 представлены спектры амплитуд входного и выходного напряжений и график АЧХ цепи, а на рис. П4.3 – спектры фаз входного и выходного напряжений и график ФЧХ цепи.
Приложение 5
Анализ колебаний в длинных линиях без потерь
Режим стоячих волн
Пример П5.1
К разомкнутой линии (рис. П5.1) длиной l = 10 м и волновым сопротивлением r = 200 Ом подключен источник гармонических колебаний с задающим напряжением U 1= 5 В. Длина волны колебаний l = 12 м. Постройте график распределения действующего значения напряжения вдоль линии. Определите Z вх.
|
| Рис. П5.1 |
Из выражения, описывающего распределение комплексного напряжения в линии без потерь, следует, что действующее значение напряжения в любой точке разомкнутой линии (I 2 = 0) может быть рассчитано так: U = U 2½cos b y ½.
Напряжение U 2в конце линии определим из условия, что 
:
В.
Рассчитаем значения напряжения в пределах изменения y от 0 до l/4. Результаты расчета сведем в табл. П5.1. В соответствии с расчетами построим график распределения действующего значения напряжения вдоль линии (рис. П5.2), учитывая при этом, что функция | cos b y | является периодической.
Определим входное сопротивление линии
Ом.
| Таблица П5.1 |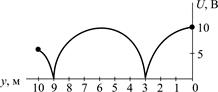 
Рис. П5.2
| ||
| b y,° | y, м | | cos b y | | U, В |
| 0,867 | 8,67 | ||
| 1,5 | 0,707 | 7,07 | |
| 0,5 | |||
Режим смешанных волн
Пример П5.2
|
| Рис. П5.3 |
Линия без потерь нагружена на резистивное сопротивление R 2 = 400 Ом (рис. П5.3).
Постройте графики распределения действующих значений напряжения и тока вдоль линии, если l = 10 м, r= 200 Ом, l = 12 м, U 1 = 5В. Определите Z вх.
Решение
Вычислим коэффициент фазы 
град/м.
Определим напряжение и ток в конце линии:
В,
мА.
Действующие значения напряжения и тока в любом сечении линии рассчитаем по формулам, которые легко получаются из уравнений передачи линии без потерь при условии, что I 2 = U 2 /R 2:
,
.
|
| Рис. П5.4 |
Графики распределения действующих значений напряжения и тока вдоль линии, построенные по результатам расчета, приведены на рис. П5.4.
Определим входное сопротивление линии:
;
;
;
Ом.
Пример П5.3
|
| Рис. П5.5 |
Воздушная линия нагружена на сопротивление Z 2 = R 2 + j w L 2(рис. П5.5). Постройте график распределения действующего значения напряжения вдоль линии, если l = 10 м, l = 12 м, r= R 2 = 200 Ом, L 2= 1,27 мкГн, U 1= 5 В. Определите Z вхи коэффициент бегущей волны в линии.
Решение
В воздушной линии скорость распространения электромагнитной волны равна скорости света c = 3×108 м/с.
Длина волны колебаний в линии l = cТ = с/f,следовательно, частоту приложенного гармонического воздействия можно определить так:
f = c /l = 3×108/12 = 0,25×108 = 25 МГц.
Рассчитаем сопротивление нагрузки на этой частоте
Z 2 = R 2 + j w L 2 = 200 + j 6,28×25×106×1,27×10–6 = (200 + j 200) Ом.
Определим ближайшее к нагрузке резонансное сечение линии y рез1 (k = 0), в котором входное сопротивление имеет резистивный характер Z = R рез.
Для этого рассчитаем коэффициент отражения
.
Резонансное сечение y рез1 для x 2 > 0 и j p > 0 определяетсятак:
м.
В этом случае
Ом.
Коэффициент бегущей волны при R рез > r
.
Если R рез > r, то напряжение в резонансном сечении линии U рез = U max.
Рассчитаем его, полагая, что линия имеет длину (l – у рез1)и нагружена на резистивное сопротивление R рез (рис. П5.5):
В следующем резонансном сечении напряжение минимально:
U min = U max K БВ = 13,2×0,383 = 5 В.
Распределение действующего значения напряжения вдоль линии будем рассчитывать так же, как для линии с резистивной нагрузкой R рез:
,
где y' – расстояние, отсчитанное влево или вправо от резонансного сечения.
На рис. П5.6 приведен график распределения действующего значения напряжения вдоль линии.
Рис. П5.6
Входное сопротивление
Ом.
Литература
Основная
1. Теория линейных электрических цепей / А.Ф. Белецкий. – М.: Радио и связь, 1986.
2. Основы теории цепей: учебник для вузов / В.П. Бакалов, В.Ф. Дмитриков, Б.Е. Крук;под. ред. В.П. Бакалова. – М.: Радио и связь, 2000. – 592 с.
Дополнительная
3. Основы теории цепей: конспект лекций. Ч.2 / В.В. Сергеев; ГОУВПО СПбГУТ. – СПб, 2003.
содержание
Введение................................................................................................................ 3
1. Классический метод анализа переходных колебаний в электрических цепях 5
1.1. Анализ переходных колебаний в разветвленных RC -цепях путем составления дифференциального уравнения 5
1.2. Анализ переходных колебаний в разветвленных RL -цепях путем составления дифференциального уравнения 8
1.3. Анализ разветвленной цепи с одним реактивным элементом
с использованием формулы 
........................... 12
1.4. Анализ свободных (переходных) колебаний
при отключении (подключении) к цепи источника гармонических колебаний...... 15
1.5. Составление уравнений переменных состояния цепи............................ 20
2. Операторный метод анализа переходных колебаний
в электрических цепях................................................................................................ 24
2.1. Анализ переходных колебаний в RC - и RL -цепях
при нулевых начальных условиях............................................................................. 24
2.2. Анализ переходных колебаний в RC -цепях
при ненулевых начальных условиях......................................................................... 28
2.3. Анализ переходных колебаний в RL -цепях
при ненулевых начальных условиях......................................................................... 31
3. Операторные передаточные функции и временные характеристики
электрических цепей................................................................................................... 36
3.1. Связь операторной передаточной функции пассивной цепи
1-го порядка с ее временными характеристиками.................................................... 37
3.2. Анализ нестационарных колебаний в цепи с использованием
переходной характеристики........................................................................................ 40
3.3. Связь между временными и частотными характеристиками активной RC -цепи 2-го порядка 41
3.4. Операторные передаточные функции
пассивных цепей 3-го порядка................................................................................... 49
4. Спектральное представление колебаний....................................................... 54
4.1. Спектры периодических негармонических колебаний.......................... 54
4.2. Анализ негармонических периодических колебаний
в электрических цепях................................................................................................ 57
4.3. Непериодические колебания. Спектральная плотность.Влияние амплитудно-частотной характеристики цепи на спектральную плотность
амплитуд воздействия................................................................................................ 60
5. Длинные линии с пренебрежимо малыми потерями.................................... 65
5.1. Режим бегущих волн в линии без потерь............................................... 66
5.2. Режим стоячих волн в линии без потерь................................................ 71
5.3. Режим смешанных волн в линии без потерь.......................................... 77
Приложения 1–5.................................................................................................. 85
Литература......................................................................................................... 114
