Операторный метод анализа переходных колебаний в ЭЦ

Таблица П2.1

Таблица соответствия функций времени (оригиналов) f (t)
и их изображений F (p)

f (t)	F (p)
A d(t)	A
A 1(t)
Ae –a t
A cos w t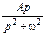
A sin w t
где
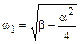
где
где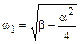

Операторные схемы замещения реактивных элементов
для ненулевых начальных условий

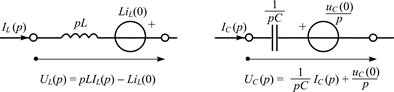
Рис. П2.1

Пример П2.1

В цепи, схема которой приведена на рис. П2.2, в момент времени t = 0 замыкается ключ. Найдите закон изменения тока в индуктивности после коммутации, если U ₀ = 10 В, L = 1 Гн, R = 10 Ом. Решите задачу операторным методом.

Решение

По закону коммутации i_L (0_–) = i_L (0₊) = U ₀/ R = 1 А. Нарисуем операторную схему замещения цепи для t > 0 (ключ замкнут) с учетом начального запаса энергии в индуктивности (рис. П2.3).

Изображение тока в этой цепи определяется по закону Ома

.

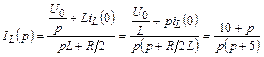Для нахождения оригинала воспользуемся теоремой разложения:

.

Тогда

.

Этому изображению соответствует оригинал

i_L (t) = 2 – e ^{–5 t}, А.

Проверка

i_L (0) = 2 – 1 = 1 А; i_L (¥) = 2 А.

Рис. П2.4

Первое значение соответствует начальным условиям задачи, второе равно установившемуся значению постоянного тока в цепи с замкнутым ключом. На рис. П2.4 показан примерный график тока в индуктивности.

Пример П2.2

Рис. П2.5

В цепи, схема которой приведена на рис. П2.5, в момент времени t = 0 размыкается ключ. Найдите закон изменения тока i_C (t) и напряжения u_C (t) после коммутации. Задачу решите операторным методом.

 

Решение

По закону коммутации u_C (0_–) = u_C (0₊) = I ₀ R /2. Для упрощения расчетов преобразуем схему цепи после коммутации (t > 0, ключ разомкнут), как показано на рис. П2.6, и нарисуем ее операторную схему замещения с дополнительным источником u_C (0)/ p, который учитывает наличие заряда на емкости к моменту коммутации (рис. П2.7).

Составим II закон Кирхгофа для операторной схемы замещения цепи (рис. П2.7) и получим выражение для изображения тока I_C (p):

,

.

Получим выражение для изображения напряжения заряженной емкости

.

Для нахождения оригинала i_C (t) воспользуемся таблицей соответствия П2.1:

.

Для нахождения оригинала u_C (t) разложим U_C (p) на сумму простых дробей

.

Найдем коэффициенты A ₁ и A ₂, приравнивая выражения

,

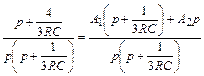где , откуда A ₁ = 4;

A ₁ + A ₂ = 1, откуда A ₂ = –3.

Тогда

.

По табл. П2.1

.

Проверка

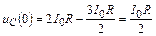, u_C (¥) = 2 I ₀ R;

, i_C (¥) = 0.

Первое значение соответствует начальным условиям задачи, второе равно установившемуся значению постоянного напряжения на емкости в цепи с разомкнутым ключом.

Рис. П2.8

На рис. П2.8 показаны примерные графики зависимостей напряжения на емкости и тока через емкость во времени.

Приложение 3

Операторные передаточные функции и временные характеристики ЭЦ

Операторная передаточная функция пассивной цепи 1-го порядка

Пример П3.1

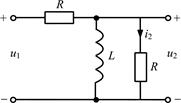
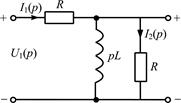
Найдите операторную передаточную функцию цепи, схема которой представлена на рис. П3.1, и соответствующие переходную h (t) и импульсную g (t) характеристики.

Рис. П3.1	Рис. П3.2

Решение

Нарисуем операторную схему замещения (рис. П3.2); начальные условия нулевые, поэтому операторная схема замещения цепи не имеет дополнительного источника.

Выразим I ₂(p) и U ₁(p) через I ₁(p):

.

Переходная характеристика цепи связана с ее передаточной функ­цией соотношением

h (t) £ .

В нашем случае

.

Импульсная характеристика цепи связана с ее передаточной функцией соотношением

g (t) £ H (p).

В нашем случае

.

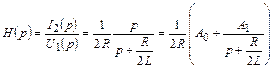Найдем коэффициенты A ₀ и А ₁, приравнивая выражения

,

где A ₀ = 1; , откуда .

Тогда

;

.

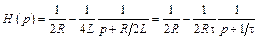Примерный график переходной характеристики h (t) для t > 0 приведен на рис. П3.3.

Рис. П3.3

Операторная передаточная функция активной цепи 2-го порядка

Пример П3.2

Найдите операторную передаточную функцию 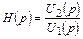цепи, схема которой представлена на рис. П3.4, и соответствующую ей переходную h (t) характеристику, если R = 100 кОм, С = 1 нФ, K = 3.

Найдите комплексную передаточную функцию H (j w) и соответствующие ей АЧХ и ФЧХ цепи. Постройте графики h (t) и АЧХ цепи и оцените связь между ними.

Убедитесь в устойчивости ARC -цепи по критерию Найквиста.

Решение

Нарисуем операторную схему замещения (рис. П3.5), заменив условное изображение усилителя с конечным усилением его схемой замещения из табл. 3.2.

Составим систему узловых уравнений для L -изображений колебаний:

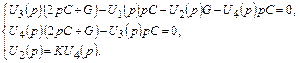
где G = .

Выразим U ₃(p) и U ₄(p) через U ₂(p):

и подставим в первое уравнение

.

После преобразования получаем

.

После подстановки заданных значений параметров

.

Найдем переходную характеристику цепи h (t):

h (t) £ ,

.

Рассчитаем значения p ₁ и p ₂:

p ² + 33,3×10³ p + 3,33×10⁷ = 0,

,

p _1,2 = –1,67×10³ ± j 5,53×10³.

Для комплексно-сопряженных корней p ₁ и p ₂ коэффициенты 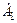и 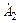тоже будут комплексно-сопряженными , т. е. достаточно рассчитать коэффициент :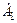

,

.

Тогда переходная характеристика цепи

,

Рис. П3.6

График h (t) рассчитан и построен с использованием программы MathCad (рис. П3.6).

Найдем граничные значения переходной характеристики цепи (рис. П3.6):

t = 0 h (0) = 1,046cos16,8 = 1,046×0,0997 = 1;

t = ¥ h (¥) = 0.

Получим комплексную передаточную функцию H (j w) и соответствующие ей амплитудно-частотную | H (j w)| и фазочастотную Q(w) характеристики:

.

.

Особенности частотных характеристик ARC -цепи 2-го порядка определяются частотой w_п и добротностью Q _п полюса передачи цепи:

, которые являются аналогами резонансной частоты w₀ и добротности Q колебательных контуров, но следует помнить, что понятие резонанса для ARC -цепей неприменимо.

Для нашего примера

.

Комплексная передаточная функция и соответствующие ей АЧХ и ФЧХ имеют вид:

.

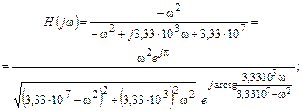
Графики АЧХ (рис. П3.7) и ФЧХ (рис. П3.8) цепи рассчитаны и построенына ПК при помощи программы MathCad.

Найдем граничные значения амплитудно-частотной характеристики | H (j w)| цепи:

w = 0 H (0) = 0; w = ¥ H (¥) = 1.

Рис. П3.7

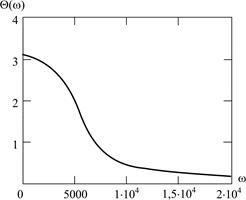
Рис. П3.8

Очевидно, что связь между временными и частотными характеристиками ARС -цепи выполняется, так как равны соотношения для их граничных значений:

,

.

Рассчитаем значения | H (j w)| на частоте полюса w_п = 5,77×10³ с^–1:

Анализ рассчитанных значений и графиков частотных характеристик показывает, что ARС -цепь 2-го порядка является электронным аналогом колебательного RLC -контура.

Для проверки ARС -цепи на устойчивость по критерию Найквиста нужно нарисовать схему цепи при закороченных входных зажимах (U ₁ = 0) и разрыве цепи на входе ОУ (рис. П3.9).

Рис. П3.9	Рис. П3.10

Нарисуем операторную схему замещения полученной цепи (рис. П 3.10) и найдем операторную передаточную функцию B (p) цепи с разомкнутой петлей ОС (петлевое усиление).

 

Составим систему узловых уравнений для L -изображений колебаний:

Используя метод подстановки, получим функцию

.

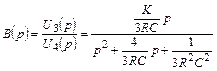Комплексная функция петлевого усиления

.

Найдем частоту w₀, на которой Jm B (j w₀) = 0 – , тогда величина Re B (j w₀) = , значит, годограф B (j w) не охватывает точку (1, j 0) на комплексной плоскости, и по критерию Найквиста данная цепь устойчива.

Годограф B (j w) петлевого усиления рассчитан и построен на ПК с использованием программы MathCad (рис. П3.11).

, w = 0,10 – 10⁶.

Рис. П3.11

Если K = 4, то цепь будет находиться строго на границе устойчивости, при этом частота собственных незатухающих колебаний w₀ =5,77×10³ с^–1.

Приложение 4