Пример 7.1
Рассчитать параметры 
, 
последовательного колебательного контура по заданной резонансной частоте 
, полосе пропускания 
и сопротивлению контура 
. Определить напряжение на входе и напряжение на всех элементах контура, если известны: ток в контуре 
, частота 
, ширина полосы пропускания 
, активное сопротивление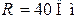 
.
Решение
Добротность контура связана с абсолютным значением полосы пропускания по формуле:
.
Характеристическое сопротивление контура:
,
откуда
;
.
Напряжение на входе контура:
.
Напряжение на активном сопротивлении, индуктивности и ёмкости соответственно равны:
;
; 
.
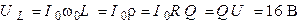Ответ: 
; 
; 
; 
; 
; 
.
Пример 7.2
Последовательный контур настроен в резонанс. Сопротивление конденсатора 
. Добротность катушки 
. Определить напряжение на конденсаторе, если напряжение приложенное к контуру,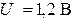 
. Определить показание вольтметра с сопротивлением 
в схеме рис.7.7.
|
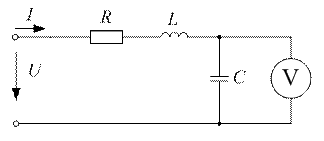
| Рис. 7.7 |
Решение
При резонансе добротность катушки будет равна добротности контура:
, 
,
отсюда
.
Напряжение на конденсаторе: 
.
При подключении вольтметра параллельно к емкости в контур внесутся дополнительные потери. На рис. 7.8 показана схема замещения, на которой параллельный участок, «конденсатор–вольтметр» заменен эквивалентным последовательным соединением 
, где
;
.
|
| Рис. 7.8 |
Так как емкостное сопротивление контура практически не изменилось 
, то не изменится и резонансная частота контура.
Определим ток в контуре:
.
Показания вольтметра определим по следующей формуле:
.
Ответ: 
.
Пример 7.3
|
Цепь рис. 7.9 находится в режиме резонанса. Мощность, потребляемая цепью  , напряжения  ,  ,  .
Определить: ,  ,  .
|
| Рис. 7.9 |
Решение
Построим векторную диаграмму напряжений, совмещённую с векторной диаграммой токов. При построении следует учитывать существующий в цепи режим резонанса напряжений, то есть вектор входного тока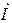 
должен совпадать по фазе с вектором входного напряжения 
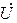. Треугольники токов и напряжений подобны. Одинаковые углы 
показаны на диаграмме (рис. 7.10). Этот факт используется при решении задачи.
|
| Рис. 7.10 |
Зная значение активной мощности, определяем значение сопротивления :
, откуда 
.
По закону Ома определяем ток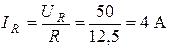 
. Из треугольника напряжений определяем угол 
.
Из треугольника токов определяем 
.
Сопротивление ёмкости определяем по закону Ома:
.
Ток 
определим как геометрическую сумму 
и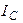 
:
.
.
Ответ: 
; 
; 
.
Пример 7.4
|
Определить токи в ветвях и в неразветвленной части схемы (рис. 7.11), а также добротность контура, если  ;  ;   .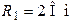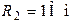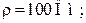
|
| Рис. 7.11 |
Решение
Волновое сопротивление контура:
.
Сопротивление ветвей параллельного контура:
;
.
Определим максимальные значения токов в ветвях по закону Ома:
;
.
Полное сопротивление контура 
является резистивным и равно:
.
Ток в неразветвлённой части цепи равен:
.
Добротность контура:
.
Ответ: 
; 
; 
; 
.
Пример 7.5
|
В цепи, изображённой на рис. 7.12, имеет место резонанс токов. Мощность, потребляемая цепью,  . Показания амперметров соответственно равны:  ,  . Определить: параметры контура , и .
|
| Рис. 7.12 |
Решение
В параллельном колебательном контуре в режиме резонанса токов равны реактивные составляющие токов параллельных ветвей в силу равенства реактивных проводимостей этих ветвей (
). Следовательно, для данной цепи справедливо соотношение:
.
Реактивные токи замыкаются в параллельном контуре, и во входной цепи протекает только активный ток:
.
На векторной диаграмме (рис. 7.13) ток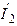 
представлен геометрической суммой активной 
и реактивной 
составляющих. Из диаграммы следует:
.
|
| Рис. 7.13 |
Мощность, потребляемая цепью, выделяется на сопротивлении , т.е.:
.
Тогда:
.
Так как 
то:
.
Напряжение на параллельном колебательном контуре:
.
Сопротивление конденсатора:
.
Из условия резонанса для параллельного контура имеем:
.
Откуда:
.
Подставляем в последнее выражение численные значения и определяем величину модулей реактивного сопротивления катушки:
;
;
.
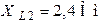Из решения следует, что резонанс токов может наступить при двух значениях индуктивного сопротивления.
Ответ: 
; 
, , .
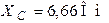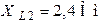Пример 7.6
|
Контур с 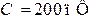 ,  питается генератором, амплитуда Э.Д.С. которого  и внутреннее сопротивление 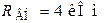 (рис. 7.14). При резонансе амплитуда напряжения на контуре равна  . Определить индуктивность и добротность контура, токи генератора и контура.
|
| Рис. 7.14 |
Решение
Определим амплитуду напряжения генератора:
.
Выражаем и рассчитываем значение тока в ветви с генератором напряжения:
.
Определим входное сопротивление параллельного контура:
.
Для контура с малыми потерями:
,
Откуда:
.
Определим характеристическое сопротивление контура:
.
Определяем добротность контура:
.
Амплитуду тока в контуре определяем исходя из следующих соотношений:
.
Ответ: 
; 
; 
; 
.
