Характеристики (показатели качества) ВК выбирают так, чтобы наиболее полно выявить свойства ВК и область его применения. При выборе показателей качества необходимо учитывать вид метрологического исследования и его цели. Выделяют три основные группы характеристик вычислительного компонента в соответствии с показателями качества (рис.3):
- характеристики точности, предназначенные для оценивания погрешности результата измерения; в том числе основные характеристики точности исходных данных, соответствующих принятым моделям и дополнительные характеристики точности для оценивания дополнительных погрешностей, обусловленных отклонениями свойств исходных данных от соответствующих принятым моделям;
- характеристики устойчивости (надежности), определяющие область работоспособности ВК;
- характеристики сложности, которые отражают вычислительные затраты при реализации ВК.
Рисунок 3 Показатели качества ВК.
При аттестации алгоритма основное внимание уделяется показателям (характеристикам) точности. Для оценивания характеристик точности необходимы сведения о моделях исходных данных и моделях погрешностей исходных данных. Первые связаны с моделями измеряемых величин, вторые - с моделью измерительного канала.
Нормирование характеристик погрешности ВК затруднено большим количеством влияющих факторов и разнообразием применяемых алгоритмов.
Перечислим алгоритмы обработки результатов прямых измерений, которые широко используются в ИИС:
- вычисление по точной формуле y = f(x1,... xn), где x1,... xn - результаты прямых измерений;
- вычисление по приближенной формуле
когда вычисление по точной формуле невозможно (например, интегрирование, преобразование Фурье и т.д.); - вычисление функций, заданных алгоритмически, когда в явном виде эту функцию записать нельзя;
- решение уравнений, в том числе операторных (здесь возможны некорректные и плохо обусловленные задачи);
- статистическая обработка результатов, в частности, непараметрическими методами, робастными алгоритмами;
- итерационные и рекуррентные процедуры (статистические, а также при помощи фильтров Калмана, алгоритмов стохастической аппроксимации, решения уравнений и т.п.);
- оптимизация процедуры.
Входными данными для всех этих алгоритмов служат результаты прямым измерений,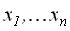 
, которые неизбежно сопровождаются погрешностями 
В данном курсе мы ограничимся анализом алгоритмов первой группы, т.е. алгоритмов с вычислениями типа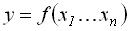 
.
