МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЦСИ ИЛИ УРАВНЕНИЕ ИЗМЕРЕНИЯ
Рассмотрим структурную модель средства измерения (СИ), приведенную на рис.6, где Д – датчик с коэффициентом преобразования Кд, АИП – аналоговый измерительный преобразователь с коэффициентом преобразования Каип, АЦП – аналого-цифровой преобразователь с уравнением измерения (при квантовании округлением)
,
(7)
где 
– числовое значение величины y; E | 
| - целая часть числа, qy – ступень квантования, sign y – знаковая функция.
Математическая модель средства измерения представляет собой зависимость между Ny и измеряемой величиной x.
(8)
Уравнение (8) неудобно для анализа из-за наличия нелинейности, обусловленной квантованием (рис.5). Поэтому уравнение (7) представляют в следующем виде
,
(9)
где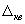 
– погрешность квантования, равная
,
(10)
где F2() – дробная часть числа.
Рис. 6. Структурная схема средства измерения.
Рис. 7. График зависимости между 
и y.
При условии, что погрешность квантования мала
,
(11)
и уравнение (8) при условии (11) представляют в окончательном виде
,
(12)
где 
,
Кп – общий коэффициент преобразования,
.
(13)
Уравнение (12) – это уравнение идеального СИ и из этого уравнения находят нормирующее значение:
.
(14)
Рис. 8. Представление уравнения измерения в виде линейной зависимости.
Рис. 9. Структурная модель СИ с источниками погрешностей.
Представление дискретизованного сигнала во временной области
Дискретизация непрерывного во времени сигнала 
является линейной операцией умножения функции на функцию во времени 
(рис. 1).
Рис. 1 Иллюстрация получения дискретизованного сигнала
Идеальный дискретизованный сигнал 
является последовательностью импульсов нулевой длительности (рис. 3а). Поэтому функцию дискретизации представляют как последовательность 
-функций или функций Дирака:
(1)
где 
-интервал дискретизации,
-дельта-функция или дельта-импульс (функция Дирака).
По определению -функция удовлетворяет следующим двум условиям:
(2)
и 
(3)
т.е. -функция равна нулю при всех отличных от нуля значениях аргумента, принимая в точке 
бесконечно большое значение. Площадь -функции равна единице.
Фильтрующее свойство -функции выражается соотношением
(4)
т.е. интеграл от произведения произвольной функции 
, ограниченной в интервале времени 
на дельта функцию 
равен значению функции в точке 
.
Результатом умножения произвольной функции на является дельта-функция, площадь которой равна значению функции в точке (рис.2).
Рис.2 Иллюстрация умножения функции на дельта функцию
Таким образом, идеальный дискретизованный сигнал является последовательностью импульсов нулевой длительности, площадь которых соответственно равна 
ординатам сигнала в моменты 
(рис. 3а), и может быть аналитически представлен в виде (5):
(5)
Реальный дискретизованный сигнал, полученный при дискретизации во времени непрерывного сигнала имеет вид импульсно-модулированного сигнала
(рис. 3б), т.е. последовательности импульсов прямоугольной формы, амплитуды которых равны значениям 
, а период следования равен 
.
Рис. 3 Дискретизованный сигнал: идеальный(а) и реальный(б)
Реальный дискретизованный сигнал может быть получен, как показано на рис.1, путем умножения непрерывного сигнала на последовательность 
единичных прямоугольных импульсов длительностью 
и периодом следования 
:
(6)
где 
– симметричный прямоугольный импульс с единичной высотой, определяемый следующим образом:
(7)
Тогда представление реального дискретизованного сигнала во временной области имеет вид:
(8)
или
(9)
