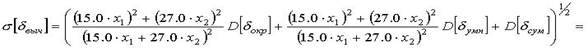Последовательность этапов оценивания характеристик погрешности вычислений приведена ниже:
· Записываем порядок проведения вычислений в соответствии с заданным алгоритмом.
· Записываем исходный алгоритм с учетом погрешностей отдельных арифметических операций.
· Находим уравнение суммарной погрешности вычислений.
· Находим математическое ожидание погрешности вычислений.
· Находим СКО погрешности вычислений.
· Находим границы доверительного интервала погрешности вычислений.
Рассмотрим приведенную последовательность на примере.
Пример 7. Найти границы погрешности вычислений с вероятностью Р=0.95 для ВК с алгоритмом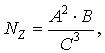 
если для вычислений использован двоичный девятиразрядный код.
Решение
Записываем порядок вычислений:
1. 
(умножение 1);
2. 
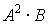(умножение 2);
3. 
(умножение 3);
4. 
(умножение 4);
5. 
(деление);
Записываем 
с учетом погрешностей отдельных операций.
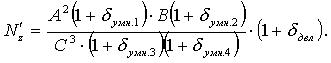
Находим уравнение суммарной погрешности вычисления в виде
Для этого записываем 
используя линеаризацию уравнения погрешности (отбрасывая составляющие второго и более высокого порядка малости).
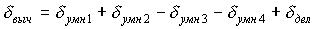
Находим математическое ожидание погрешности вычислений.
Если используется система с плавающей запятой и с округлением, то в соответствии с п.2.1 
Тогда в соответствии с п.2.2
Если вычисление погрешности производят для фиксированного значения С, то
Т.к. n=9, 
Находим дисперсию погрешности вычислений.
Находим СКО погрешности вычислений.
Находим границы доверительного интервала погрешности вычислений, предполагая что распределение суммарной погрешности нормальное.
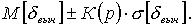
При Р=0.95 К(р)=2, и,таким образом, нижняя граница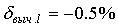 
, а верхняя граница 
.
Для нормирования из двух модулей берут больший и окончательно считают,что погрешность вычислений не превосходит 0.5% с вероятностью Р=0.95.
Следует отметить, что погрешность вычислений зависит от последовательности вычислений. Рассмотрим второй вариант решения примера при последовательности вычислений:
1. 
(деление 1);
2. (деление 2);
3. 
(умножение 1);
4. 
(деление 3);
5. 
(умножение 2);
Записываем с учетом погрешностей отдельных операций.
Уравнение суммарной погрешности вычислений
.
Математическое ожидание погрешности вычислений
Среднеквадратическое отклонение погрешности вычислений
Находим нижнюю и верхнюю границы погрешности вычислений:
; 
Погрешность вычислений не превосходит 1.3.% с вероятностью Р=0.95.
Пример 8. Найти выражения для характеристик погрешности алгоритма:
Решение
Пример 9. Найти выражение для характеристик погрешности алгоритма
Решение
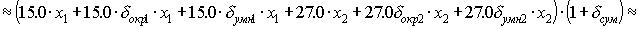
(для округления)
