Таким образом, возникают два случая восстановления непрерывного сигнала из дискретизированного:
· по физическому дискретизированному во времени сигналу;
· по известным числовым значениям дискретизированного сигнала в соответствующие моменты дискретизации 
.
Первый случай характерен главным образом для устройств техники связи и реализуется путем восстановления физических промежуточных значений величины, второй характерен для цифровых измерительных устройств.
Во втором случае приближенно восстанавливаются, т.е. аппроксимируются, числовые значения величины в промежуточные моменты времени. Восстановление сигнала в обоих случаях должно проводится с заданной погрешностью.
Рассмотрим более подробно второй случай восстановления. При восстановлении сигнала необходимо прежде всего предварительно подобрать для данного участка сигнала восстанавливающую базисную функцию. При этом восстанавливаемый сигнал обычно выражается суммой базисных функций:
,
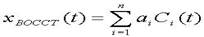(1)
где 
- некоторая система базисных функций, которая обычно является ортогональной или ортонормированной;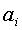 
- коэффициенты ряда.
Коэффициенты ряда 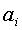и базисные функции могут выбираться на основе различных критериев, например по минимуму средней квадратической погрешности или по критерию совпадения восстанавливаемого непрерывного сигнала с мгновенными значениями дискретизированного сигнала.
Координаты времени базисных функций могут изменяться в широком диапазоне, например, на всем протяжении интервала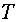 
-времени реализации данного сигнала либо только на протяжении одного или нескольких интервалов дискретизации 
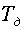. Естественно, что базисные функции подбираются прежде всего из условий наибольшей простоты их реализации, при этом желательно также, чтобы коэффициенты ряда 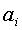определялись бы простейшим способом по параметрам дискретизированного сигнала, в частности, по мгновенным значениям дискретизированного сигнала.
Наиболее часто применяемой восстанавливающей функцией является ряд В.А. Котельникова, который далее будет рассмотрен подробнее.
Часто встречается ситуация, когда в качестве базисных функций используются степенные полиномы (ступенчатая, кусочно-линейная, параболическая аппроксимации). Эти виды аппроксимации получили широкое применение в измерительной технике, т.к. они удобны для аналитического восстановления с помощью ЭВМ на основе числовых результатов измерения параметров дискретизированного сигнала.
