Погрешностью квантования ЦСИ 
является разность между результатом измерения 
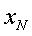и истинным значением измеряемой величины 
, если все звенья ЦСИ идеальны и не имеют погрешностей. Погрешность квантования возникает от несовершенства самого измерения как вида отражения, поскольку в этом случае непрерывный размер выражается в ограниченном множестве чисел – результатов измерения.
Погрешность квантования обычно аддитивна по характеру, т.е. не зависит от .
Статистические характеристики погрешности квантования определяются алгоритмом квантования.
Для алгоритма квантования (1) погрешность квантования равна
,
(4)
где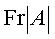 
- дробная часть А.
Распределение погрешности 
равномерное и расположено в области отрицательных значений аргумента, т.к.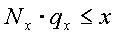 
. В этом случае максимальная погрешность 
(рис.3а). Математическое ожидание погрешности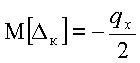 
. СКО погрешности равно 
.
Рис.3. Распределения погрешности квантования при различных алгоритмах квантования.
Для алгоритма квантования (2) погрешность квантования равна
,
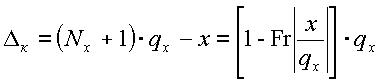(5)
Распределение погрешности равномерно, но расположено в области положительных значений (рис.3б).
Максимальное значение погрешности 
.
Математическое ожидание погрешности равно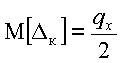 
, а СКО равно .
Для алгоритма квантования (3) погрешность квантования равна
.
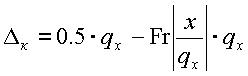(6)
Распределение погрешности квантования в этом случае равномерное в интервале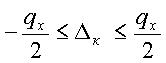 
рис.3в). Максимальное значение погрешности 
(рис.3а). Математическое ожидание погрешности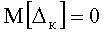 
.
СКО погрешности равно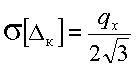 
.
В любом ЦСИ с цифровым отсчетным устройством предусмотрено определенное количество десятичных разрядов. Если во всех разрядах используются все десять возможных состояний, соответствующих цифрам от 0 до 9, то максимальное число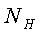 
, которое может индицироваться на цифровом отсчетном устройстве из трех десятичных разрядов,составляет 999, а при четырех разрядах 9999 и т.д. Но встречаются случаи, когда старший разряд является неполным. Например, есть цифровые вольтметры, у которых в старшем разряде 0 или 1, а в остальных трех - все десять состояний. В этом случае N=1999. Значение 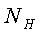называют номинальным числом ступеней квантования. При этом максимальное значение измеряемой величины (предел измерения) 
.
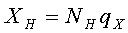При регламентациикласса точности для ЦСИ исользуют приведенную погрешность квантования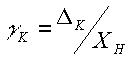 
. Тогда максимальное значение приведенной погрешности квантования (для алгоритма квантования) равно 
.
Если 
(для алгоритмов квантования 1, 2) максимальное значение приведенной погрешности квантования равно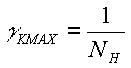 
.
Если в аналого-цифровом преобразователе (АЦП) измеряемая величина представляется в двоичном коде, то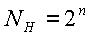 
, где n -число двоичных разрядов.
В этом случае для алгоритма квантования 3
,
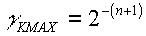а для алгоритмов квантования 1,2
.
