Дифференциальное уравнение преобразователя
Схема преобразователя приведена на рис.1
Формально дифференциальное уравнение преобразователя первого порядка можно представить в виде:
, 
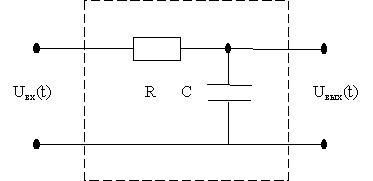
Рис.1. Схема преобразователя.
Для преобразователя рис.1.
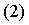
откуда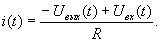 
Исключаем промежуточную переменную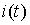 
, подставляя (3) в приведенное ниже соотношение
, 
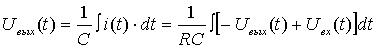Возьмем производную левой и правой части уравнения (4)
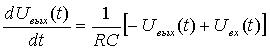
Откуда получаем дифференциальное уравнение в виде
, 
Сравнивая (1) и (5) получаем
, где 
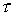- постоянная времени преобразователя; S0=1.
Представляем дифференциальное уравнение преобразователя в
окончательном виде
.
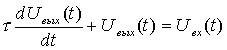1.2 Передаточная функция преобразователя
Операторное изображение дифференциального уравнения имеет вид
.
Откуда передаточная функция преобразователя равна
.
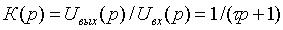1.3 Амплитудно-фазовая характристика
Амплитудно-фазовая характеристика имеет вид
.
1.15.4 Совокупность амплитудно-частотной и фазочастотной характеристик.
Амплитудно-частотную характеристику получаем с помощью следующих преобразований
.
Тогда
. 
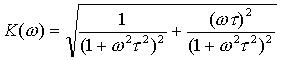После преобразований
.
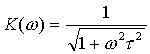График АЧХ приведен на рис.2.
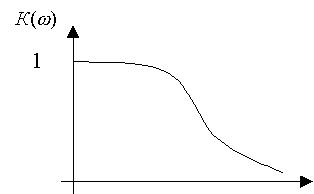
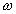
Рис.2.Амплитудно-частотная характеристика апериодического преобразователя.
Фазо-частотную характеристику получаем в следующем виде:
.
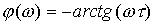График ФЧХ приведен на рис.3.
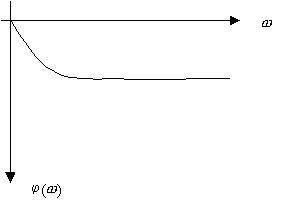
Рис.3.Фазо-частотная характеристика апериодического преобразователя.
Импульсная характеристика преобразователя
Импульсную характеристику получаем из выражения для К(р)
Используя таблицу обратного преобразования Лапласа
,
получим:
.
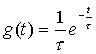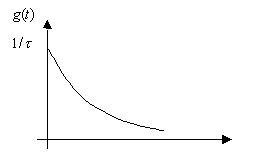
График g(t) приведен на рис.4.
t
Рис.4.Импульсная характеристика апериодического преобразователя.
Переходная характеристика
Переходную характеристику получаем из соотношения
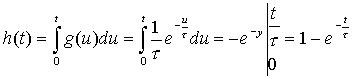
Окончательно 
.
График h(t) приведен на рис.5.
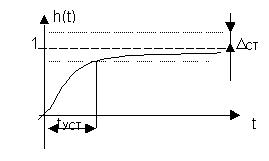
Рис.5.Переходная характеристика апериодического преобразователя.
Время установления
Найдем частную динамическую характеристику – время установления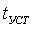 
переходной характеристики 
СИТ.
Время установления - это время, по прошествии которого отклонение переходной характеристики от установившегося значения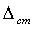 
не превышают заданного значения.
Для определения 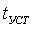нужно решить уравнение
;
; 
.
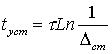Если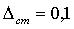 
(что эквивалентно относительной статической погрешности 
), 
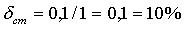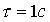, то время установления равно 
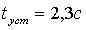. Если 
(это эквивалентно 
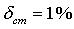), то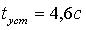 
.
1.16. Динамические характеристики преобразователя второго порядка.
1.16.1 Дифференциальное уравнение
Пусть общий вид дифференциального уравнения преобразователя второго порядка определяется выражением:
, 
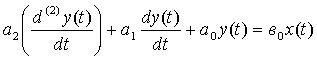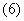
Если в качестве конкретного примера использовать магнитоэлектрический преобразователь, то входной и выходной сигнал и коэффициенты дифференциального уравнения приобретают конкретный физический смысл:
, где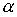 
– угол поворота подвижной части подвижной катушки преобразователя; 
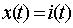, где i(t) – ток, протекающий по катушке, 
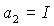, где I – момент инерции подвижной части, 
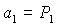, где Р – коэффициент успокоения, 
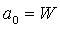, где W – удельный противодействующий момент, 
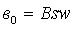, где В – индукция в воздушном зазоре, s – площадь катушки, w – число витков катушки.
Тогда уравнение (6) принимает следующий вид
, 
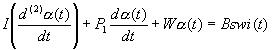Если правую и левую часть уравнения (7) разделить на I и ввести частные динамические характеристики: частоту собственных колебаний подвижной части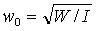 
и степень успокоения 
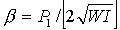, то дифференциальное уравнение преобразователя можно представить в окончательном виде
.
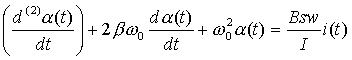Передаточная функция
Операторное изображение дифференциального уравнения имеет вид:
.
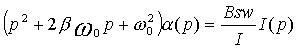Отсюда передаточная функция имеет вид
.
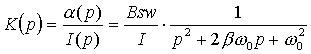1.16.3 Амплитудно-фазовая характеристика
Амплитудно-фазовая характеристика, как зависимость от 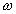, имеет вид:
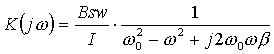
Для преобразователей второго порядка удобно представлять амплитудно-фазовую характеристику как функцию относительной частоты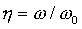 
. В этом случае амплитудно-фазовая характеристика принимает вид:
.
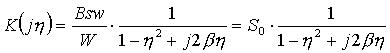Тогда АЧХ и ФЧХ определяются следующим образом:
;
;
.
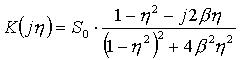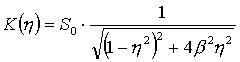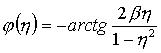График зависимости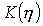 
показан на рис.6. Из формулы и рисунка видно, что степень успокоения 
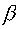существенно влияет на динамические свойства механизма. На рисунке показаны три
зависимости 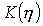: первая кривая для 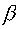<0.5; вторая-для 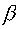>0.5; третья-для 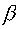=0.5.
При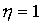 
(т.е. 
) = 
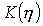. Тогда для частот вблизи к 
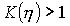, т.е. амплитуда колебаний на выходе больше амплитуды колебаний на входе. Таким образом в этой области проявляются резонансные свойства механизма.
При 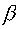>0.5(или 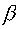=0.5) функция 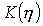для 
убывает равномерно с большей или меньшей скоростью.
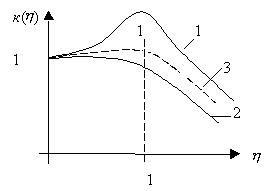
Рис.6. АЧХ преобразователя второго порядка.
От значений коэфициента успокоения зависит и переходная характеристика, когда на вход подается скачек, тогда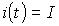 
.
