Поэтому при расчете режимов местных электрических сетей с номинальным напряжением 35 кВ и ниже используется ряд допущений, которые существенно упрощают их расчеты и одновременно не приводят к значительным погрешностям результатов расчета. Рассмотрим их.
1. В схемах замещения линий при расчете их режимов не учитывается зарядная мощность 
.
Ее пропускная способность по условию нагрева длительно допустимым током 
составляет
Значит доля зарядной мощности в пропускной способности линии всего
Эта величина очень мала и ее неучет не скажется на точности расчета режима.
При отсутствии зарядной мощности схема замещения линии станет более простой, что упростит расчет режима местной электрической сети.
2. Для кабельной линии в схеме замещения можно пренебречь индуктивным сопротивлением 
. В кабелях токопроводящие жилы расположены близко одна к другой и магнитный поток, сцепляющийся с жилой, мал. Поэтому мало и вызванное им индуктивное сопротивление. Только при достаточно больших сечениях жил (
) индуктивное сопротивление кабеля соизмеримо с его активным сопротивлением
3. Не учитываются потери холостого хода трансформаторов.
4. При расчете режима напряжения пренебрегают поперечной потерей составляющей падения напряжения 
. Они учитывают лишь продольную составляющую падения напряжения, которая принимается равной потере напряжения. При заданном напряжении в начале звена 
потери напряжения равны
Для местных электрических сетей характерны достаточно малые отклонения напряжения от номинального значения Это объясняется требованиями, предъявляемыми подключенными к ним потребителями, к качеству электроэнергии. В соответствии с ними на зажимах электроприемников должны обеспечиваться нормально допустимые отклонения напряжения, равные 
. Поэтому при расчете потерь напряжения значение напряжения во всех точках сети принимается равным номинальному 
. Таким образом расчет потери напряжения на всех участках сети ведется не по действительным напряжениям, а по номинальному
5. При расчете потоков мощности не учитываются потери мощности в сети. Если по сопротивлению схемы замещения звена (рис.6.13, а) протекает ток 
, то для начала его
;
для конца
Так как напряжения в местной сети мало отличаются от номинального и, если, как сделано при расчете потерь напряжения, принять 
, то получим, что мощность 
в начале звена равна мощности 
в конце его (
).
11.
12. Расчет режим электрических сетей при известных U1, S2 при неизвестных U2, S1
Известны мощность в конце звена S 2 и напряжение в начале звена U1. Требуется найти мощность в начале звена S 1 и напряжение в конце U 2. Этот случай наиболее чаще встречается в практике, так как обычно известно напряжение на шинах источника питания (электростанции, понижающей подстанции), от которого отходят линии с заданными нагрузками потребителей в конце.
Здесь невозможно, используя формулу (6.12) сразу вычислить напряжение U 2, так как неизвестна мощность в начале звена S 1. Нельзя также на основании формулы (6.10) точно определить S 1, так как для расчета потерь мощность по выражению (6.11) неизвестно напряжение в конце звена U2. Поэтому расчет ведут методом последовательных приближений. Исходя из величины напряжения U1, задают начальное приближение напряжения в конце U2=U2(0). Если нет конкретных соображений по выбору величины U2(0), ее принимают равной номинальному напряжению сети. Тогда, зная U2(0), по формулам (6.11) и (6.10) можно найти первое приближение потерь мощности в начале звена
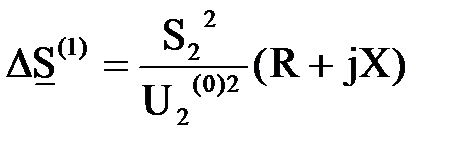; (6.18)
. (6.19)
Теперь по выражению (6.12) можно найти первое приближение напряжения в конце звена
. (6.20)
Подставляя в формулу (6.18) модуль напряжения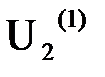 
, находят потери мощности в звене во втором приближении. Затем повторяют расчет по формулам (6.19) и (6.20). Расчет заканчивают, если разность между модулями напряжений 
последнего и предыдущего приближений не больше заданной точности расчета.
При этом без применения ЭВМ обычно ограничиваются расчетом первого приближения напряжения 
и мощности 
.
13.
14.
15.
