Построим векторную диаграмму применительно к рис.6.1, а, которой соответствует полная П-образная схема замещения, приведенная на рис.6.1, б. Пусть в конце линии включена нагрузка, заданная током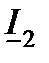 
, которая имеет активно-индуктивный характер. При построении диаграммы будем использовать фазные параметры (
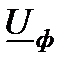и 
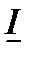). Примем, что напряжение 
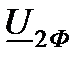направлено по действительной оси (рис.6.1. в), тогда можно записать 
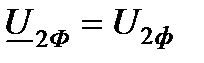. При заданном характере нагрузки вектор тока 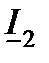отстает от напряжения 
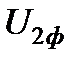на угол 
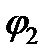. По закону Ома токи в активной и реактивной проводимостях в конце линии соответственно равны
; 
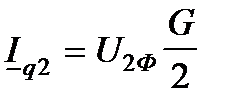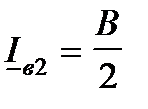
Вектор тока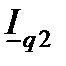 
имеет активный характер, поэтому отложен от конца вектора 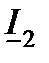по направлению, совпадающим с вектором 
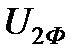. Ток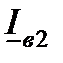 
носит емкостной характер, поэтому он опережает на 90° напряжение 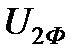и отложен от конца вектора 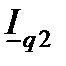.В результате получен ток 
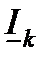, протекающий в сопротивлениях R и Х лини. Фактически ток в линии 
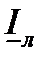в соответствии с первым законом Кирхгофа равен
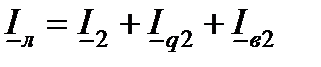
Напряжение в начале линии по закону Ома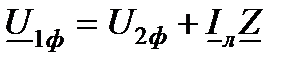 
,
где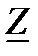 
- полное сопротивление линии, 
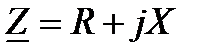. Или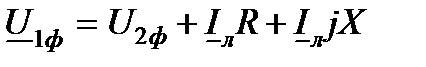 
.
В соответствии с последним выражением к концу напряжения 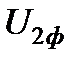пристроим вектор 
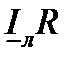, совпадающий по направлению с вектором тока 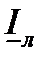, и от конца вектора 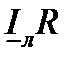отложим вектор 
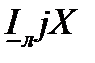, опережающий вектор тока 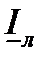на 90°. Вектор, соединяющий начало координат О и конец вектора 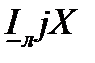, является вектором фазного напряжения 
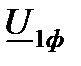в начале линии.
Токи в проводимостях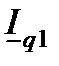 
и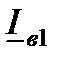 
найдем аналогично токам 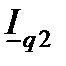и 
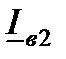по закону Ома 
; 
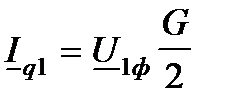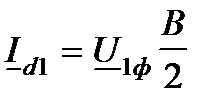
Ток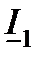 
в начале линии определится по первому закону Кирхгофа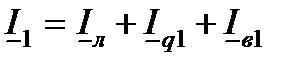 
Для получения его по векторной диаграмме, к концу вектора тока 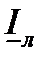пристроим вектор тока в активной проводимости 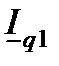, совпадающий по направлению с вектором напряжения 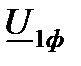, и к концу 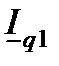добавим вектор тока в реактивной проводимости 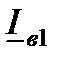, опережающий вектор 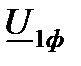на 90°. Вектор, соединяющий начало координат О и конец вектора 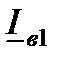и есть ток в начале линии 
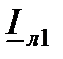. Из диаграммы (рис.6.1. в) видно. Что между векторам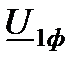и 
и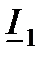 
образовался угол 
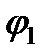. Напряжение 
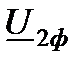в конце линии меньше, чем напряжение 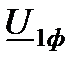в начале. При этом разность векторов напряжений 
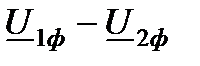равна вектору 
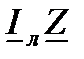, который называется падением напряжения. Падение напряжения - геометрическая разность векторов напряжений в начале и конце линии электропередачи. На векторной диаграмме (рис.6.1, в) соответствует вектору АВ. Из точки В опустим перпендикуляр на действительную ось и точку их пересечения обозначим С. Как видно. В прямоугольном треугольнике АВС падение напряжения (гипотенуза АВ) имеет две составляющие (катеты АС и СВ). Вектор АС, по направлению совпадающий с вектором напряжения 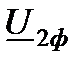, называется продольной составляющей падения напряжения, а вектор СВ, направленный перпендикулярно напряжению 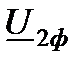, поперечной составляющей падения напряжения.
Используя векторную диаграмму (рис.6.1, г), получим аналитические выражения для определения падения напряжения и его составляющих.
Продольная составляющая падения напряжения АС может быть представлена в виде АС=АЕ+ЕС
Из треугольника АЕD АЕ=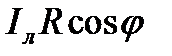 
Из треугольника DВF DF=ЕС=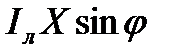 
Тогда АС=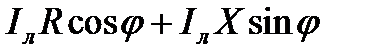 
= 
;
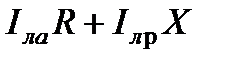где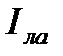 
и 
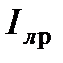- соответственно активная и реактивная составляющие тока 
.
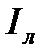Поперечная составляющая падения напряжения СВ может быть записана в виде СВ= FB-EC
Cоответственно из треугольников DBF и AED
FB=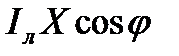 
; ED=FC=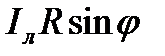 
Значит СВ= - =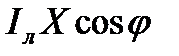 
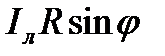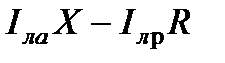
Таким образом, продольную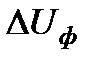 
и поперечную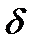 
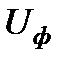составляющие падения напряжения можно определить по формулам
; 
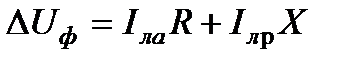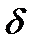
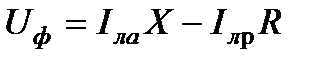(6.1)
Полученную величину падения напряжения можно записать в виде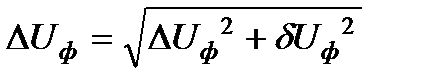 
Связь между напряжениями начала и конца линии в комплексной форме можно представить так
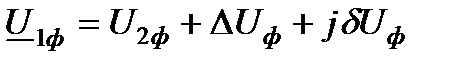(6.2)
Величину напряжения в начале линии можно найти через напряжение в конце линии и составляющие падения напряжения из треугольника ОВС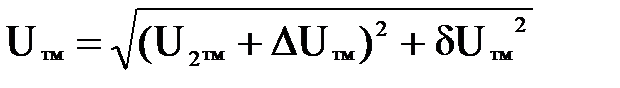 
(6.3)
Из второго уравнения (6.1) видно, что при некоторых условиях (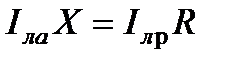
) поперечная составляющая падения напряжения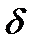 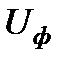превращается в нуль. Фактически это имеет место, когда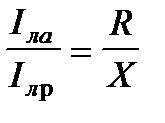 
В этом случае вектора напряжени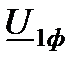й и 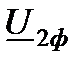совпадают по направлению и по величине отличаются на продольную составляющую падения напряжения 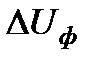. Практически это встречается в линиях низких и средних напряжений, где действительное соотношение составляющих тока 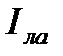и 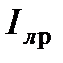и сопротивлений линий R и X делают 
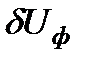малой величиной.
Отметим, что алгебраическая разность напряжений в начале и конце линии по величине (модулю) называется потерей напряжения. Для пояснения потери напряжения на векторной диаграмме (рис.6.1, в) совместим поворотом относительно точки О вектор напряжения 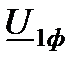с напряжением 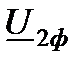. Он примет положение ОК. Разность величин отрезков ОК и ОА и есть потеря напряжения. Заметим, что при 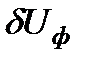=0 потеря напряжения фактически равна продольной составляющей падения напряжения.
На рис. 6.1, г несколько подробней дан фрагмент векторной диаграммы токов. Ток нагрузки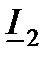 
, который, как отмечалось, имеет активно-индуктивный характер, разложен на активную 
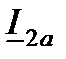и реактивную 
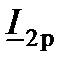составляющие. Аналогично в виде двух составляющих (
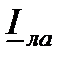и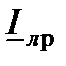 
) представлен ток в линии 
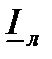. Как видно из диаграммы, ток 
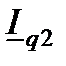, обусловленный активной проводимостью линии, увеличивает активную составляющую тока нагрузки 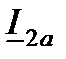, а емкостной ток 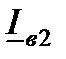, вызванный реактивной проводимостью линии, уменьшает реактивную составляющую тока нагрузки .
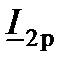Аналогично построены векторные диаграммы (рис.6.2, б и 6.3, б) для линий электропередачи, схемы замещения которых соответственно приведены на рис. 6.3, а и 6.4, а. На рис.6.3 в схеме замещения отсутствует активная проводимость, что в большей степени соответствует воздушным линиям напряжением 110 и 220 кВ. Схема замещения в соответствии с рис.6.3 применяется для линий распределительных сетей напряжением 35 кВ и ниже.
Определенный интерес представляет векторная диаграмма напряжений и токов линии, схема замещения которой включает емкостную проводимость (рис.6.2, а), при отсутствии нагрузки в конце линии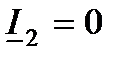 
. В этом случае по сопротивлениям линии R и X в направлении с конца к началу протекает емкостной ток 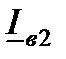, опережающий напряжение 
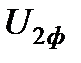на 90° (рис.6.4). По закону Ома 
.
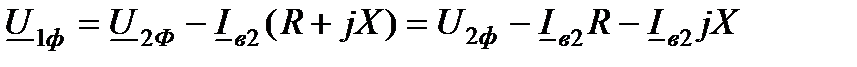В соответствии с этим выражением на рис.6.4 построен вектор напряжения 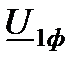, как видно в режиме холостого хода напряжение в конце линии 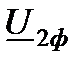больше, чем в начале 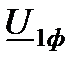, а при отсутствии тока нагрузки 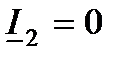в начале линии протекает ток 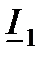, имеющий емкостной характер.
|
Рис. 1. Векторная диаграмма линии электропередачи
5.Расчет режим электрических сетей при известных U2, S2 при неизвестных U1, S1.
Известны неизменные мощность и напряжение в конце звена: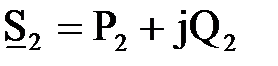 
и 
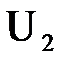. Требуется определить мощность 
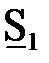и напряжение 
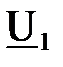в начале звена.
Здесь и далее расчет будем вести в линейных напряжениях.
Совмещая вектор напряжения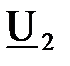 
с векторной осью, на основании закона Ома запишем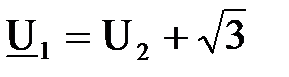 
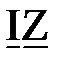(6.4)
где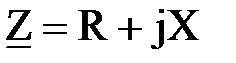 
- полное сопротивление.
Так как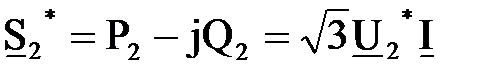 
,
то получим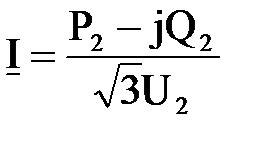 
.
Тогда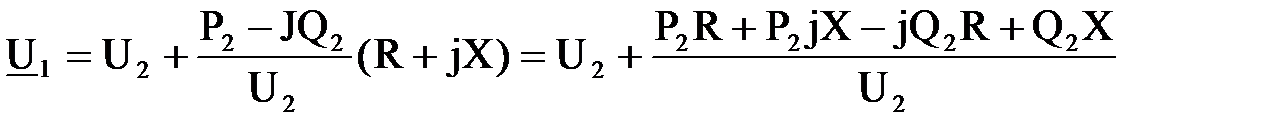 
.
После преобразований
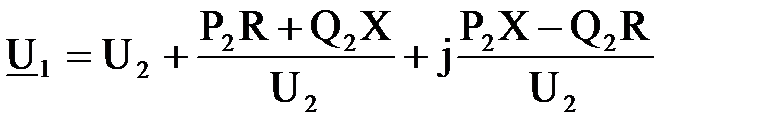; (6.5)
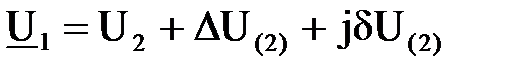, (6.6)
где продольная составляющая падения напряжения, вычисленная по данным конца звена, равна
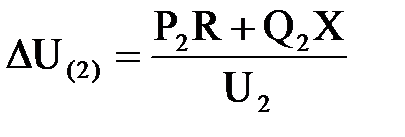(6.7)
и поперечная составляющая падения напряжения
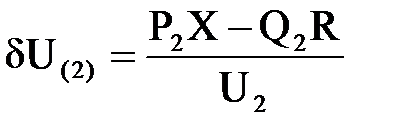. (6.8)
Модуль напряжения в начале звена
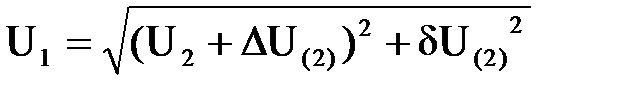. (6.9)
Векторная диаграмма напряжений для этого случая показана на рис.6.6, а.
Умножив обе части выражения (6.4) на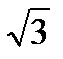 
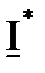, получим
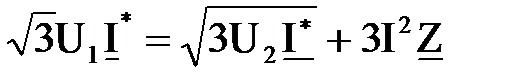или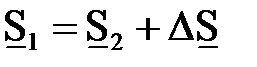 
. (6.10)
Таким образом мощность в начале звена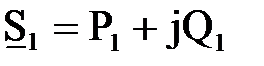 
и потерь мощности в конце 
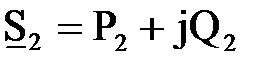и потерь мощности в звене 
.
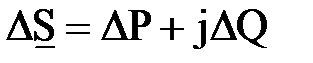Потери мощности, найденные по данным конца звена
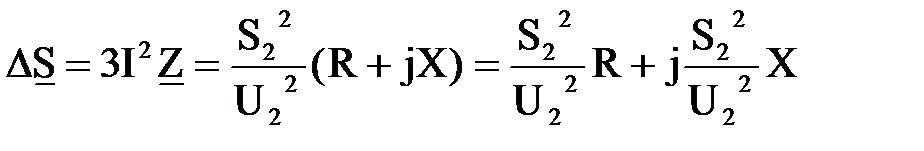. (6.11)
Потери активной и реактивной мощности в звене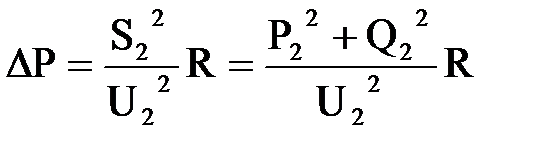 
;
.
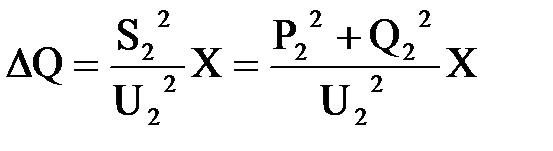6. Расчет режим электрических сетей при известных U1, S1 при неизвестных U2, S2
Второй случай. Известны мощность и напряжение в начале звена: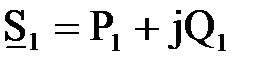 
и 
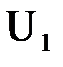. Требуется определить мощность 
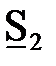и напряжение 
в конце звена.
Как и для первого случая по закону Ома можно записать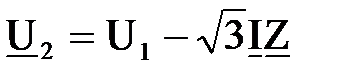 
.
Ток найдем по формуле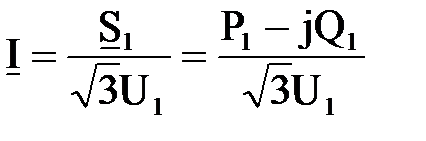 
.
Тогда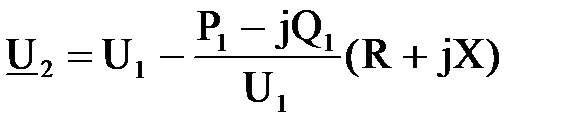 
.
Раскрыв скобки и преобразовав, получим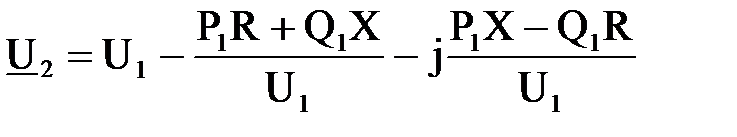 
(6.12)
Или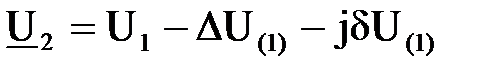 
. (6.13)
Здесь продольная и поперечная составляющие падения напряжения определяются по данным начала
; 
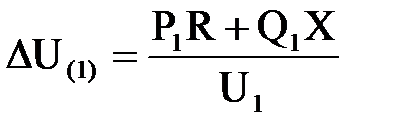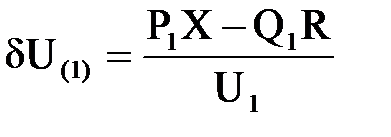. (6.14)
Величина напряжения в конце звена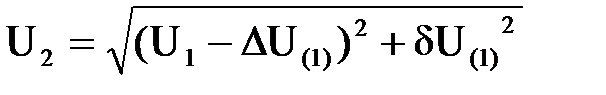 
. (6.15)
Векторная диаграмма напряжений для данного случая приведена на рис. 6.6, б.
Продольные и поперечные составляющие падения напряжения, вычисленные по данным конца звена (формулы (6.7) и (6.8)) не равны, т.е. 
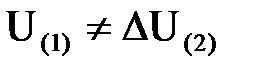и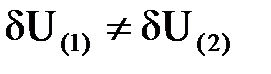 
; что также наглядно видно из совмещенной векторной диаграммы, приведенной на рис. 6.6, в.
Мощность в конце звена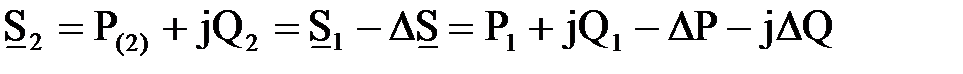 
. (6.16)
Здесь потери мощности, выраженные через параметры начала звена
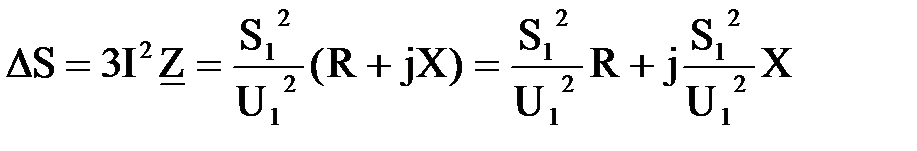. (6.17)
Потери активной и реактивной мощности в звене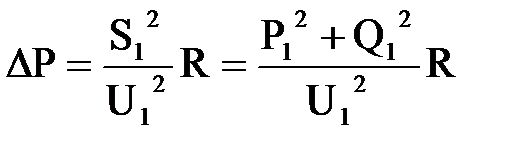 
,
.
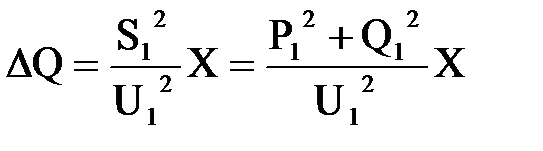Метод контурных уравнений
По. методу контурных уравнений расчет ведется в два этапа: сначала определяется потокораспределение мощностей по участкам без учета потерь мощности сети, а затем рассчитываются напряжения узлов, потери мощности и потокораспределение с учетом потерь мощности.
Для нахождения потокораспределения без учета потерь используются контурные уравнения мощности. Основой этих уравнений является второй закон Кирхгофа, согласно которому для замкнутого контура, не содержащего ЭДС, можно записать:
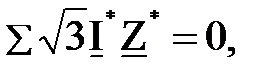
где I * ‑ ток участка контура, Z * ‑ его полное сопротивление.
Если обе части этого уравнения умножить на некоторое среднее напряжение сети и допустить, что произведение тока каждого участка на это напряжение дает значение комплекса полной мощности этого участка, можно получить контурное уравнение в мощностях:
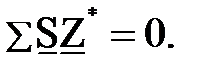(8.30)
В рассматриваемом случае ограничимся этим уравнением, которое чаще всего оказывается достаточным.
Уравнение (8.30) в комплексных числах можно представить выражением
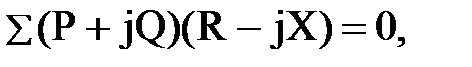
которое после преобразования может быть заменено двумя уравнениями с вещественными величинами:
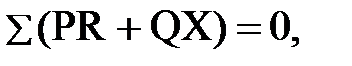(8.31)
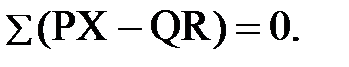(8.32)
