Теплове випромінювання
1. Закон Стефана - Больцмана для абсолютно чорного тіла
R = sT4,
де R - інтегральна випромінювальна здатність, або енергетична світимість абсолютно чорного тіла;
s - стала Стефана - Больцмана (s = 5,67×10-8 Вт/м2 ×К4);
Т - термодинамічна температура тіла.
2. Закон Стефана - Больцмана для сірого тіла
Rc = asT4,
де a - поглинальна здатність тіла, яка визначається відношенням поглинутої енергії до падаючої.
3. Закон Кірхгoфа
,
де en,T - спектральна випромінювальна здатність будь-якого тіла;
an,T - спектральна поглинальна здатність будь-якого тіла;
rn,T - стала величина для всіх тіл, називається спектральною випромінювальною здатністю абсолютно чорного тіла.
4. Закон зміщення Віна
lmax = 
,
де lmax - довжина хвилі, на якій енергія випромінювання абсолютно чорного тіла досягає максимуму;
b - стала Віна (b = 2,9×10-3 м×К);
Т - термодинамічна температура.
5. Формула Планка через частоту n випромінювання:
,
де rn,T – спектральна випромінювальна здатність абсолютно чорного тіла при температурі Т і в діапазоні частот від ν до ν + dν;
n - частота випромінювання;
с - швидкість світла;
hn - енергія кванта;
k - стала Больцмана (k = 1.38×10-23 Дж/К);
h - стала Планка (h = 6.62×10-34 Дж×с);
Т - термодинамічна температура.
6. Формула Планка через довжину хвилі l
.
7. Залежність максимальної спектральної густини випромінювання абсолютно чорного тіла від температури:
(rl,T)max = c × T5,
де с - стала величина (с = 1,30×10-5 Вт/м2К5).
Приклад 17. Абсолютно чорне тіло знаходиться при температурі 2900К. В результаті охолодження довжина хвилі, на яку припадає максимум спектральної густини випромінювальної здатності тіла, зменшилась на Dl = 9 мкм. До якої температури було охолоджено тіло?
Дано:
Т1 = 2900 К
Dl = 9 мкм
-------------------
Т2 -?
Розв`язування: Згідно закону Віна, довжина хвилі, на яку припадає максимум спектральної густини випромінювальної здатності абсолютно чорного тіла, розраховується за формулою
lmax = 
.
Після охолодження довжина хвилі, на яку припадає максимум спектральної густини випромінювальної здатності, зросте на величину Dl:
(l + Dl)max = 
.
Після нескладних перетворень одержуємо:
Звідки
T2 = 
.
Підставимо числові значення
= 290 (K).
Відповідь: Т2 = 290 К.
Приклад 18. Температура Т абсолютно чорного тіла дорівнює 2000 К. Визначити спектральну густину випромінювальної здатності rl,T для довжини xвилі l = 600 нм.
Дано:
Т = 2000 К
l = 600 нм
--------------------
rl,T -?
Розв`язування: Скористаємось формулою Планка через довжину хвилі l
,
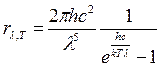де h = 6,62×10-34 Дж×с; c = 3×108 м/с; к = 1,38×10-23 Дж/К; l = 600 нм; Т = 2000 К.
Підставимо числові значення
T2 = 
= 29,8×1010 Вт/м3.
Відповідь: rl,T = 29.8×1010 Вт/м3.
Приклад 19. Потужність випромінювання абсолютно чорного тіла дорівнює 10 кВт. Визначити величину поверхні випромінювання, якщо відомо, що довжина хвилі, на яку припадає максимум спектральної густини його випромінювальної здатності, дорівнює 7×10-7 м.
Дано:
Р = 10 кВт
lmax = 7×10-7 м
--------------------------
S -?
Розв`язування: Інтегральна випромінювальна здатність aбсо лютно чорного тіла дорівнює
R = 
, (1)
де W - повна енергія випромінювання; S - величина поверхні випромінювання; Dt - час випромінювання.
Згідно з законом Стефана - Больцмана інтегральну випромінювальну здатність абсолютно чорного тіла визначають також за формулою:
R = s T4, (2)
де s - стала Стефана - Больцмана;
Т - термодинамічна температура.
Значення термодинамічної температури знаходять із закону зміщення Віна:
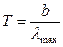, (3)
де b - стала Віна.
Прирівнюючи праві частини формул (1) і (2) та враховуючи (3), знаходимо площу випромінювання
,
де 
- потужність випромінювання.
Отже, одержуємо:
S = 
.
Підставимо числові значення
S = 
= 5,98 × 10-4 м2.
Відповідь: S = 5,98×10-4 м2» 6 см2.
Приклад 20. Обчислити температуру поверхні Сонця, якщо відомо, що сонячна стала, яка дорівнює потужності енергії випромінювання на один м2 площини, що розміщена перпендикулярно до сонячного проміння біля поверхні Землі, становить 1,4×103 Вт/м2.
Дано:
С = 1,4 ×103 Вт/м2.
Т -?.
Розв`язування: Зв`язок енергії випромінювання з одиниці площі поверхні Сонця за одиницю часу, з температурою випромінювання дається законом Стефана - Больцмана
R = s T4,
Енергія, яка випромінюється всією поверхнею Сонця, дорівнює
W = sT4 4pr2,
де r - радіус Сонця.
Величину цієї енергії можна розрахувати також через сонячну сталу, помножену на площу поверхні радіусом, рівним відстані від Землі до Сонця,
W = C4pR2,
де С - сонячна стала;
R - радіус земної орбіти.
Прирівнюючи праві частини цих рівностей та розв`язуючи одержане рівняння відносно температури, знаходимо
T = 
.
Підставимо числові значення
= 5800 K
Відповідь: Т = 5800 К.
Фотоефект
1. Енергія фотона:
e = hn = 
,
де h - стала Планка;
n - частота світлових хвиль;
l - довжина хвилі;
с - швидкість світла.
2. Маса рухомого фотона (маса спокою фотона дорівнює нулю, фотон в спокої не існує):
m = 
.
3. Імпульс фотона:
p = 
.
4. Формула Ейнштейна для фотоефекту:
,
де hn - енергія фотона;
А - робота виходу електрона з металу;
- максимальна кінетична енергія фотоелектрона.
5. Червона межа фотоефекту:
або l0 = 
,
де n0 - найменша частота світла, при якій ще можливий фотоефект;
l0 - найбільша довжина хвилі, при якій ще можливий фотоефект.
6. Формула Ейнштейна для фотонів, енергія яких спів розмірна з енергією спокою електрона (роботою виходу нехтують)
hn = E0 × 
,
де Е0 = m0с2 - енергія спокою електрона;
- відношення швидкості руху електрона до величини швидкості світла.
Приклад 21. Визначити максимальну швидкість vmax фотоелектронів, які вилітають з поверхні металу під дією g - випромінювання з довжиною хвилі l = 0,3 нм.
Дано:
l = 0,3 нм
v max -?
Розв`язування: В залежності від швидкості фотоелектронів максимальна кінетична енергія їх може бути розрахована або за класичною формулою
Kmax = 
,
або за релятивістською формулою
K = m0c2 
.
Критерієм вибору тієї чи іншої формули є співвідношення між енергією падаючого фотона і енергією спокою електрона.
Знайдемо енергію падаючого фотона на поверхню металу
e = 
0,04 (МеВ).
Енергія спокою електрона
= 0,51 (МеВ).
Енергія падаючого фотона ще значно менша енергії спокою електрона. Тому можна користуватись як класичною, так і релятивістською формулами кінетичної енергії.
а) в релятивістському випадку
e = E0 
.
Швидкість фотоелектронів дорівнюватиме
υ = 
,
де Е0 = m0с2; e = hn.
Підставимо числові значення
υ = 
=
= 3.79 ×107 (м/с)
б) в класичному випадку, нехтуючи роботою виходу,
e = 
, звідки υmax = 
.
Підставимо числові значення
υmax = 
= 3,8 × 107 (м/с).
Відповідь: υ = 3.8×107 м/с.
Тиск світла
1. Тиск світла при перпендикулярному падінні на поверхню тіла визначається за допомогою формули
p = 
або p = w (1+r),
де Е0 - енергія всіх фотонів, які падають на одиницю площі за одиницю часу;
r - коефіцієнт відбивання (для дзеркального тіла r = 1, для чорного тіла r = 0);
с - швидкість світла;
w - об`ємна густина енергії.
Приклад 22. Лазер випромінює в імпульсі протягом t = 0,134 мс промінь світла енергією W = 10 Дж. Визначити середній тиск такого світлового імпульсу, якщо його сфокусувати на невелику пляму діаметром d = 10 мкм на деякій поверхні, перпендикулярно до проміння, з коефіцієнтом відбивання r = 0,5.
Дано:
t = 0,13 мс
W = 10 Дж
d = 10 мкм
r = 0,5
----------------------
р -?
Розв`язування: При дії квантів світла на деяку поверхню половина з них поглинається, а друга половина - відбивається, змінюючи свій імпульс на протилежний.
Зміна імпульсу всіх фотонів за час одного імпульсу випромінювання лазера дорівнює
Dк = 2 
,
де 2 
- зміна імпульсу відбитих фотонів;
- зміна імпульсу поглинутих фотонів.
Або
D к = 
,
де W = Nhn.
За другим законом Ньютона
Dk = Ft,
де F - середня сила, з якою фотони діють на деяку поверхню;
t - час дії сили, який рівний часу одного імпульсу випромінювання лазера.
Звідки
Ft = .
Тиск світлового імпульсу
p = 
де S =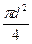 
.
Підставимо числові значення
P = 
= 4,89 × 106 Па.
Відповідь: Р = 4,89 ×106 Па.
Ефект Комптона
1. Формула ефекту Компотна має вигляд
Dl = l‘ - l = 
,
або
Dl = l‘ - l = 
,
де l - довжина хвилі фотона, який падає на вільний або зв`язаний
електрон;
l` - довжина хвилі розсіяного під кутом q фотона;
m0 - маса спокою електрона.
2. Комптонівська довжина хвилі електрона
, /L = 2,436 × 10-3 м/.
Приклад 23. Рентгенівські промені з довжиною хвилі l = 70,8 нм здійснюють комптонівське розсіювання на вільних електронах. Визначити довжину хвилі рентгенівських променів, розсіяних в напрямках:
а) p/2; б) p.
Дано:
l = 70,8 пм
q1 = p/2
q2 = p
---------------------
l1 -? l2 -?
Розв`язування: Зв`язок довжини хвиль падаючих і розсіяних фотонів подається формулою Комптона
l1 = l + .
Підставимо числові значення (cos 
= 0)
а)
l1 = 70,8 × 10-12 + 
= 73,2 × 10-12 (м).
б)
l2 = 70,8 × 10-12 + 
× (1 - cos 180°) =
= 75,64 ×10-12 (м).
Відповідь: l1 = 73,2 пм; l2 = 75,64 пм.
Задачі
398. Кожний інтерференційний максимум, який створюється на екрані двома когерентними джерелами білого світла, є багатоколірним з червоним зовнішнім (l = 0,7 мкм) і фіолетовим внутрішнім (l = 0,4 мкм) краями. Яка ширина першого максимуму, якщо відстань між джерелами світла 4 мм, а їх відстань до екрана 4 м?
Відповідь: 0,3 мм.
399. У скільки разів збільшиться відстань між сусідніми інтерференційними смугами на екрані в досліді Юнга, якщо зелений світлофільтр (l1 = 5×10-7 м) замінити червоним ( l2 = 6,5×10-7 м)?
Відповідь: в 1,3 разу.
400. Відстань між двома когерентними джерелами 1,1 мм, а відстань від джерел до екрана 2,5 м. Джерела випромінюють монохроматичне світло з довжиною хвилі 5,5×10‑7 м. Визначити число інтерференційних смуг на 1 см довжини екрана.
Відповідь: N = 8.
401. У досліді Юнга щілини освітлювались монохроматичним світлом з довжиною хвилі l = 6,0×10-7 м. Відстань між щілинами 1 мм, а відстань від щілин до екрана 3 м. Знайти положення трьох перших світлих смуг.
Відповідь: у1 = 1.8 мм; у2 = 3.6 мм; у3 = 5.4 мм.
402. Різниця ходу двох когерентних променів 2.5 мкм. Визначити довжини хвиль видимого світла (від 700 нм до 400 нм), які дають інтерференційні максимуми.
Відповідь: 625 нм; 500 нм; 417 нм.
403. На шляху одного з інтерферуючих променів у досліді Юнга помістили тонку скляну (n = 1.5) пластинку товщиною 2.5 мкм. Промінь світла падає на пластинку перпендикулярно. На скільки світлових смуг зміщується інтерференційна картина на екрані, якщо довжина світлової хвилі l = 6,5×10-7 м?
Відповідь: 2.
404. Знайти довжину хвилі світла, яке падає на дзеркала Френеля, якщо відстань між двома уявними зображеннями джерела світла в дзеркалах дорівнює 0,7 мм. Відстань уявних зображень до екрана 2,267 м, а на 1,9 см довжини екрана знаходиться 10 світлих інтерференційних смуг.
Відповідь: 0,58 мкм.
405. Знайти довжину хвилі світла, яке освітлює установку в досліді Юнга, якщо на шляху одного з інтерферуючих променів поміщено скляну пластинку (n = 1,52) товщиною 3 мкм, в результаті чого картина інтерференції змістилась на екрані на три світлих смуги.
Відповідь: l = 5,2×10-7 м.
406. Різниця ходу інтерферуючих хвиль від двох когерентних джерел світла дорівнює 0,2 довжини хвилі. Визначити різницю фаз цих хвиль.
Відповідь: 720
407. Два когерентних джерела, відстань між якими 0,2 мм, розташовані на відстані 1,5 м від екрана. Знайти довжину світлової хвилі, якщо третій мінімум розташований на екрані на відстані 12,6 мм від центра інтерференційної картини.
Відповідь: 5,6×10-7 м.
408. В досліді з дзеркалами Френеля відстань між уявними зображеннями джерела світла 0,5 мм. Відстань від уявних зображень до екрана 5 м. Знайти відстань між сусідніми інтерференційними максимумами, якщо довжина хвилі світла 5×10-7 м.
Відповідь: 5 мм.
409. Відстань двох когерентних джерел від екрана 1,5 м, відстань між ними 0,18 мм. Скільки світлих смуг розміститься на відрізку довжиною 1 см від центра інтерференційної картини. Довжина хвилі світла 6×10-7 м.
Відповідь: 2.
410. Для усунення відбивання світла на поверхню скляної лінзи наносять плівку речовини з показником заломлювання 1,2, меншим, ніж у скла. При якій найменшій товщині такої плівки відбите світло з довжиною хвилі 0,6 мкм не буде спостерігатися, якщо світло падає перпендикулярно?
Відповідь: 1,25×10-7 м.
411. Знайти найменший кут падіння монохроматичного світла (l = 0,5 мкм) на мильну плівку (n = 1,3) товщиною 0,1 мкм, яка, перебуваючи в повітрі в прохідному світлі, здається темною.
Відповідь:» 21о.
412. Мильна плівка завтовшки 0,104 мкм освітлюється промінням Сонця. Яке забарвлення матиме плівка у відбитому світлі (к=0), якщо кут відбивання 35о, а показник заломлювання плівки 1,33?
Відповідь: зелене; l = 5×10-7м.
413. На тонку мильну плівку (n1 = 1,3) товщиною 1,25 мкм падає перпендикулярно монохроматичне світло. У відбитому світлі плівка здається світлою. Якої найменшої товщини необхідно взяти іншу тонку плівку (n2 = 1,48), щоб вона за цих же умов здавалась темною?
Відповідь: 2,2 мкм.
414. На мильну плівку однакової товщини (n = 1,33) падає біле світло під кутом a = 45о. При якій найменший товщині h плівки відбите від неї світло буде зеленим (l = 550 нм)?
Відповідь: 1,22×10-7 м.
415. На мильну плівку падає світло під кутом 60о. При якій найменшій товщині плівки відбиті промені будуть забарвлені в червоний колір (l =0,65 мкм)? Показник заломлювання мильної води 1,33.
Відповідь: 1,61×10-7 м.
416. На поверхню скляної пластинки (n = 1,5) нанесена прозора плівка (n = 1,4), яка освітлюється перпендикулярно світлом з довжиною хвилі 6×10-7 м. Яку найменшу товщину повинна мати плівка для того, щоб не було відбивання світла?
Відповідь: 1,0×10-7 м.
417. Промінь монохроматичного світла (l = 5,5×10-7 м) падає перпендикулярно на тонку плівку, яка нанесена на скляну пластинку. Показники заломлювання плівки і скла відповідно рівні 1,46 і 1,54. Визначити найменшу товщину плівки, яка забезпечує максимальне ослаблення відбитого світла.
Відповідь: 94 нм.
418. Монохроматичний промінь з довжиною хвилі 6×10-7 м падає на мильну плівку під кутом 45о. Показник заломлювання мильної води 1,33. При якій найменший товщині плівки відбите від неї світло буде максимально ослаблене?
Відповідь: 5,3×10-7 м.
418. На мильну плівку товщиною 0,15 мкм падає перпендикулярно біле світло. Якого кольору буде плівка у відбитому і прохідному світлі? Показник переломлення плівки n = 1,33.
Відповідь: 
Фіолетовий.
420. На тонкий скляний клин падає перпендикулярно пучок променів з довжиною хвилі 0,6 мкм. Кут між поверхнями клина 
. Показник заломлення скла клина - 1,5. Яке число темних смуг приходиться на одиницю довжини клина?
Відповідь:
421. На шляху світлової хвилі, яка поширюється в повітрі, поставили скляну пластинку товщиною 1 мм. Як зміниться оптична довжина шляху, якщо хвиля падає на пластинку під кутом 30o? Показник заломлення скла n = 1,5.
Відповідь:
422. Пучок білого світла падає перпендикулярно на скляну пластинку, товщина якої 0,4 мкм. Показник заломлення скла n = 1,5. Які довжини хвиль, що лежать у межах видимого спектра (від 4·10-7 м до 7,8·10-7 м) підсилюються у відбитому пучку?
Відповідь:
423. У скількох разів збільшиться відстань між сусідніми інтерференційними смугами на екрані в досліді Юнга, якщо зелений світлофільтр (λ1 = 5·10-7 м) замінити червоним (λ2 = 6,5·10-7 м)?
Відповідь:
424. У досліді Юнга отвори освітлюються монохроматичним світлом з довжиною хвилі λ = 6·10-5 см. Відстань між отворами d = 1 мм і відстань від отворів до екрана L = 3 м. Знайти відстані до трьох перших максимумів, починаючи від нульового.
Відповідь:
425. Знайти довжину хвилі λ монохроматичного випромінювання, якщо в досліді Юнга відстань між першим і нульовим інтерференційними максимумами х = 0,05 см, відстань від щілин до екрана L = 5 м, а відстань між щілинами d = 0,5 см.
Відповідь:
426. На тонку плівку (n = 1,33) падає рівнобіжний пучок білого світла. Кут падіння α = 60o. При якій товщині плівки відбите світло найбільше сильно пофарбоване в жовтий колір (λ = 0,60 мкм)?
Відповідь:
427. Мильна плівка освітлюється випромінюванням, яке має такий спектральний склад: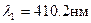 
; 
; 
; 
. Спостереження ведеться у відбитому світлі. Які світлові хвилі λ будуть максимально підсилені, а які максимально ослаблені в результаті інтерференції, якщо товщина плівки d = 0,615 мкм? Світло падає перпендикулярно до поверхні плівки. Показник заломлення мильної рідини n = 1,33.
Відповідь:
428. Знайти мінімальну товщину dmin плівки з показником заломлення n = 1,33, при якій світло з довжиною хвилі λ1 = 0,64 мкм буде повністю відбиватися, а світло з довжиною хвилі λ2 = 0,40 мкм буде повністю поглинатися. Кут падіння світла α = 30o.
Відповідь:
429. На плівку з гліцерину (n = 1,5) товщиною 0,3 мкм падає біле світло. Яким буде здаватися колір плівки у відбитому світлі, якщо кут падіння променів 45о?
Відповідь: k = 2; l = 5,29×10-7 м.
430. На тонкий скляний клин падає перпендикулярно монохроматичне світло з довжиною хвилі 6×10-7 м. Відстань між суміжними інтерференційними смугами дорівнює 2 мм. Знайти кут між поверхнями клина.
Відповідь: 20,5”.
431. Між плоско-паралельними скляними пластинками лежить дротина, внаслідок чого між ними утворився клин, який заповнили рідиною з показником заломлювання 1,5 (меншим за показник заломлювання скла). У відбитому світлі з довжиною хвилі 5×10-7 м спостерігається інтерференційна картина у вигляді смуг, відстань між якими 5 мм. Знайти кут між пластинками клина.
Відповідь: 6,8”.
432. На тонкий скляний клин перпендикулярно падає світло з довжиною хвилі 6×10-7 м. Відстань між суміжними інтерференційними смугами у відбитому світлі дорівнює 0,5 мм. Показник заломлювання скла 1,5. Визначити кут між поверхнями клина.
Відповідь: 1,37¢.
433. Радіус другого темного кільця Ньютона у відбитому світлі r2 = 0,4 мм. Визначити радіус R кривизни плоско-опуклої лінзи взятої для досліду, якщо вона освітлюється монохроматичним світлом з довжиною хвилі l = 0,64 мкм.
Відповідь: 0,125 м.
434. Пристрій для спостереження кілець Ньютона освітлюється монохроматичним світлом, яке падає перпендикулярно. Довжина хвилі світла 0,5 мкм. Знайти радіус кривизни лінзи, якщо діаметр п¢ятого світлого кільця у прохідному світлі дорівнює 10 мм.
Відповідь: R = 10,0 м.
435. На скляну пластину покладена опуклою стороною плоско-опукла лінза. Радіус п¢ятнадцятого темного кільця Ньютона у відбитому світлі (l = 0,6 мкм) дорівнює 3 мм. Знайти оптичну силу лінзи.
Відповідь: 0,5 діоптрій.
436. Кільця Ньютона утворюються між плоским склом та лінзою з радіусом кривизни 12,1 м. Монохроматичне світло падає перпендикулярно. Діаметр одинадцятого світлого кільця у відбитому світлі дорівнює 6,6 мм. Знайти довжину хвилі падаючого світла.
Відповідь: 6×10-7 м.
437. Плоско-опукла лінза з оптичною силою 2 діоптрії лежить опуклою стороною на плоскій скляній пластинці. Радіус четвертого темного кільця у відбитому світлі дорівнює 0,7 мм. Визначити довжину світлової хвилі.
Відповідь: 4,9×10-7 м.
438. У пристрої для спостереження кілець Ньютона простір між лінзою і скляною пластинкою заповнено рідиною. Визначити показник заломлювання рідини, якщо діаметр третього темного кільця у відбитому світлі дорівнює 7мм. Світло з довжиною хвилі 6,0×10-7 м падає перпендикулярно. Радіус кривизни лінзи 10 м.
Відповідь: n = 1,47°.
439. Відстань між першим та другим світлими кільцями Ньютона при спостереженні їх у відбитому світлі дорівнює 0,5 мм. Знайти відстань між десятим та одинадцятим кільцями.
Відповідь 0,152 мм.
440. У досліді з інтерферометром Майкельсона для зміщення інтерференційної картини на 500 смуг потрібно було змістити дзеркало на відстань 0,161 мм. Чому дорівнює довжина хвилі інтерферуючого світла?
Відповідь: 6,44 × 10-7 м.
441. В інтерферометрі Майкельсона переміщенням одного із дзеркал інтерференційна картина змінюється на 200 смуг. Довжина хвилі 5×10-7 м. На яку відстань було зміщено дзеркало?
Відповідь: 0,05 мм.
442. На якій найменшій відстані від діафрагми з круглим отвором радіусом 0,6 мм необхідно розмістити екран, щоб при освітленні отвору паралельним пучком променів (l = 0,6 мкм) в центрі дифракційної картини на екрані спостерігалась темна пляма?
Відповідь: 0,3 м.
443. Дифракційна картина спостерігається на відстані 1 м від точкового джерела монохроматичного світла (l = 0,5 мкм). Посередині між екраном і джерелом світла розміщено діафрагму з круглим отвором. При якому найменшому радіусі отвору центр дифракційної картини буде темним?
Відповідь k = 2; r = 5×10-4 м.
444. Світло від монохроматичного джерела (l = 0,6 мкм) падає перпендикулярно на діафрагму з круглим отвором. Діаметр отвору 6 мм. За діафрагмою на відстані 3 м від неї знаходиться екран. Скільки зон Френеля вкладається в отвір діафрагми? Яким буде центр дифракційної картини на екрані - темним чи світлим?
Відповідь: 5, світлий.
445. Знайти площу будь-якої зони Френеля у випадку сферичного хвильового фронту, якщо відстань від центральної зони до точки спостереження 5 м, а радіус кривизни хвильового фронту 3 м і довжина світлової хвилі 0,5 мкм.
Відповідь: 2,94 мм2
446. Обчислити радіуси перших трьох зон Френеля, якщо відстань від джерела світла до хвильової поверхні 1м, відстань від хвильової поверхні до точки спостереження також 1м та l = 0,5 мкм.
Відповідь: 0,5; 0,71; 0,86 (мм).
447. Світло від монохроматичного джерела (l = 0,6 мкм) падає перпендикулярно на діафрагму з круглим отвором діаметром 1,2 мм. Темним чи світлим буде центр дифракційної картини на екрані, який знаходиться на відстані 0,3 м від діафрагми?
Відповідь: k = 2, темний.
448. Обчислити розділи перших трьох зон Френеля для випадку плоскої хвилі. Відстань від хвильової поверхні до точки спостереження 1 м. Довжина хвилі 0,5 мкм.
Відповідь: 0,71; 1,00; 1,23 (мм).
449. Дифракційна картина спостерігається на відстані l від точкового джерела монохроматичного світла (l = 0,6 мкм). На відстані 0,5 l від джерела розташовано круглу непрозору перешкоду діаметром 1 см. Чому дорівнює відстань l, якщо перешкода закриває тільки центральну зону Френеля?
Відповідь: 83 м.
450. Дифракційна картина спостерігається на відстані 4 м від точкового джерела монохроматичного світла (l = 0,5 мкм). Посередині між екраном та джерелом світла розташовано діафрагму з круглим отвором. При якому радіусі отвору центр дифракційної картини на екрані буде найбільш темним?
Відповідь: 1,41 мм.
451. На відстані 20,35 м від щита з отвором, діаметр якого 10 мм встановлено екран для спостереження дифракції світла (l = 0,614 мкм). Визначити - темна чи світла пляма буде знаходитись в центрі дифракційної картини.
Відповідь: k = 2; темна.
452. На щілину шириною 0,1 мм падає перпендикулярно монохроматичне світло, яке відповідає довжині хвилі 0,7 мкм. Визначити кут відхилення променів для першого дифракційного максимуму.
Відповідь: 36’.
453. Монохроматичне світло (l = 0.5 мкм) падає перпендикулярно паралельним пучком на пластинку з щілиною. Знайти відхилення променів, яке відповідає першому дифракційному мінімуму, якщо ширина щілин 0,1 мм. Чому дорівнюватиме цей кут, якщо ширину щілини зробити рівною 1 мм?
Відповідь:» 17,7’;» 1,17’.
454. На щілину шириною 2 мкм перпендикулярно падає паралельний промінь монохроматичного світла (l = 589 нм). Під якими кутами будуть спостерігатись дифракційні мінімуми світла?
Відповідь: 17,8°; 36,5°; 62°.
455. На щілину шириною 0,2 мм падає перпендикулярно паралельний пучок монохроматичного світла з довжиною хвилі 0,6 мкм. Знайти відстань між першими дифракційними мінімумами на екрані, який знаходиться на відстані 0,5 м від щілини.
Відповідь: 3×10-3 м.
456. На щілину шириною 6 l перпендикулярно падає паралельний промінь монохроматичного світла. Під яким кутом буде спостерігатись третій дифракційний мінімум?
Відповідь: 30°
457. На непрозору пластинку з щілиною падає перпендикулярно паралельний промінь світла з довжиною хвилі 0,6 мкм. Ширина щілини 0,25 мм. Знайти кут відхилення променів, який відповідає першому дифракційному максимуму.
Відповідь: 12,4°.
458. Промінь монохроматичного світла з довжиною хвилі 0,76 мкм падає перпендикулярно на вузьку щілину, створюючи перший дифракційний мінімум під кутом 14°30`. Визначити ширину щілини.
Відповідь: 3 мкм.
459. Яку кількість рисок на одиницю довжини має дифракційна решітка, якщо зелена лінія ртуті (l = 546,1 нм) в спектрі першого порядку спостерігається під кутом 19,8°?
Відповідь: 626 мм-1.
460. При освітленні дифракційної решітки білим світлом спектри другого та третього порядків накладаються. На яку довжину хвилі в спектрі третього порядку накладається червона межа (l =780 нм) в спектрі другого порядку?
Відповідь: 520 нм.
461. На мильну плівку товщиною 0,15 мкм падає перпендикулярно біле світло. Якого кольору буде плівка у відбитому і прохідному світлі? Показник переломлення плівки n = 1,33.
Відповідь: Фіолетовий.
462. На тонкий скляний клин падає перпендикулярно пучок променів з довжиною хвилі 0,6 мкм. Кут між поверхнями клина . Показник заломлення скла клина - 1,5. Яке число темних смуг приходиться на одиницю довжини клина?
Відповідь:
463. На шляху світлової хвилі, яка поширюється в повітрі, поставили скляну пластинку товщиною 1 мм. Як зміниться оптична довжина шляху, якщо хвиля падає на пластинку під кутом 30o? Показник заломлення скла n = 1,5.
Відповідь:
464. Пучок білого світла падає перпендикулярно на скляну пластинку, товщина якої 0,4 мкм. Показник заломлення скла n = 1,5. Які довжини хвиль, що лежать у межах видимого спектра (від 4·10-7 м до 7,8·10-7 м) підсилюються у відбитому пучку?
Відповідь:
465. У скількох разів збільшиться відстань між сусідніми інтерференційними смугами на екрані в досліді Юнга, якщо зелений світлофільтр (λ1 = 5·10-7 м) замінити червоним (λ2 = 6,5·10-7 м)?
Відповідь:
466. У досліді Юнга отвори освітлюються монохроматичним світлом з довжиною хвилі λ = 6·10-5 см. Відстань між отворами d = 1 мм і відстань від отворів до екрана L = 3 м. Знайти відстані до трьох перших максимумів, починаючи від нульового.
Відповідь:
467. Знайти довжину хвилі λ монохроматичного випромінювання, якщо в досліді Юнга відстань між першим і нульовим інтерференційними максимумами х = 0,05 см, відстань від щілин до екрана L = 5 м, а відстань між щілинами d = 0,5 см.
Відповідь:
468. На тонку плівку (n = 1,33) падає рівнобіжний пучок білого світла. Кут падіння α = 60o. При якій товщині плівки відбите світло найбільше сильно пофарбоване в жовтий колір (λ = 0,60 мкм)?
Відповідь:
469. Мильна плівка освітлюється випромінюванням, яке має такий спектральний склад: 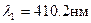; ; ; . Спостереження ведеться у відбитому світлі. Які світлові хвилі λ будуть максимально підсилені, а які максимально ослаблені в результаті інтерференції, якщо товщина плівки d = 0,615 мкм? Світло падає перпендикулярно до поверхні плівки. Показник заломлення мильної рідини n = 1,33.
Відповідь:
470. Знайти мінімальну товщину dmin плівки з показником заломлення n = 1,33, при якій світло з довжиною хвилі λ1 = 0,64 мкм буде повністю відбиватися, а світло з довжиною хвилі λ2 = 0,40 мкм буде повністю поглинатися. Кут падіння світла α = 30o.
Відповідь:
471. На дифракційну решітку падає перпендикулярно промінь світла від газорозрядної трубки. Якою повинна бути стала d дифракційної решітки, щоб в напрямку j = 41° співпадали максимуми ліній l1 = 656,3 нм та l2 = 410,2 нм?
Відповідь: d = 5 мкм.
472. На дифракційну решітку падає перпендикулярно монохроматичний промінь світла (l = 0,59 мкм), причому спектр третього порядку спостерігається під кутом 10°12`. При якій довжині світлової хвилі дифракційний спектр першого порядку буде спостерігатись під кутом 2°48’.
Відповідь: 0,490 мкм.
473. На дифракційну решітку падає перпендикулярно промінь світла від газорозрядної трубки, наповненої гелієм. На яку лінію в спектрі третього порядку накладається червона лінія гелію (l = 670 нм) в спектрі другого порядку?
Відповідь: 447 нм; синя лінія гелію.
474. На дифракційну решітку з періодом 4,8 мкм світло падає перпендикулярно. Які спектральні лінії, що їм відповідають довжини хвиль, які лежать в межах видимого спектра, будуть співпадати в напрямі j = 30°?
Відповідь: 800; 600; 480; 400 нм.
475. Знайти найбільший порядок спектра для жовтої лінії натрію (l = 589 нм), якщо стала дифракційної решітки d = 2 мкм.
Відповідь: 3.
476. На дифракційну решітку падає перпендикулярно монохроматичне світло з довжиною хвилі 600 нм. Решітка має 200 смуг на міліметр. Визначити число дифракційних максимумів, які утворюються в цьому випадку.
Відповідь: 17.
477. На дифракційну решітку падає перпендикулярно промінь монохроматичного світла. Максимум третього порядку спостерігається під кутом 36,48°. Визначити сталу решітки в довжинах хвиль падаючого світла.
Відповідь: d/l = 5.
478. Скільки смуг на 1 см довжини має дифракційна решітка, якщо зелена лінія ртуті (l = 546 нм) у спектрі першого порядку спостерігається під кутом 19°8`?
Відповідь: 6000 см-1.
479. Одна з найкращих дифракційних решіток має 2000 смуг на один міліметр. Визначити напрямок максимуму в спектрі першого порядку для блакитних променів (l = 480 нм).
Відповідь: 73,46°.
480. Скільки смуг на сантиметр має дифракційна решітка, якщо спектр четвертого порядку, який утворюється нею при перпендикулярному падінні світла з довжиною хвилі 650 нм, спостерігається під кутом 60°.
Відповідь: 3330 см-1.
481. Визначити найбільший порядок спектра, загальне число головних максимумів в дифракційній картині та кут дифракції у спектрі третього порядку при перпендикулярному падінні монохроматичного світла з довжиною хвилі 0,59 мкм. Стала дифракційної решітки 2.5 мкм.
Відповідь: N = 9; kmax = 4; j = 45°.
482. На екрані одержано дифракційні спектри за допомогою решітки, яка має 500 смуг на один міліметр та розташована паралельно до екрана. Вважаючи, що граничні довжини хвиль, що їх сприймає око людини, знаходяться в інтервалі 0,39 мкм - 0,78 мкм, знайти ширину спектра першого порядку, якщо екран знаходиться на відстані 1,8 м від решітки.
Відповідь: 35,1 см.
483. Дифракційна решітка має 117 смуг на 1 мм довжини. Визначити довжину хвилі монохроматичного світла, яке падає перпендикулярно на решітку, якщо кут між двома спектрами другого порядку 16°.
Відповідь: 0,598 мкм.
484. На дифракційну решітку падає перпендикулярно промінь монохроматичного світла з довжиною хвилі 0,59 мкм. Під якими кутами будуть спостерігатись дифракційні максимуми першого та другого порядків, якщо решітка має 500 смуг на міліметр?
Відповідь: 17°; 36°.
485. Скільки смуг повинна мати дифракційна решітка, щоб з її допомогою можна було розділити у третьому порядку лінії кадмію 288,12 нм та 288,078 нм?
Відповідь:» 2300.
486. Чому повинна дорівнювати ширина дифракційної решітки з періодом 20 мкм, щоб у спектрі першого порядку був розділений дублет l1 = 404,4 нм та l2 = 404,7 нм?
Відповідь: 2,7 см.
487. Дифракційна решітка шириною 3 см має сталу решітки 3 мкм. Яка її роздільна здатність у спектрі другого порядку? Чому дорівнює різниця довжин двох найближчих хвиль, які розділяються у спектрі другого порядку, якщо довжина однієї із хвиль 500 нм?
Відповідь: 20000; 0,025 нм.
488. Яку різницю довжин хвиль можна бачити роздільно за допомогою дифракційної решітки шириною 2 см та періодом 5 мкм в області червоних променів (l = 0.7 мкм) у спектрі другого порядку?
Відповідь: Dl = 8,75 нм.
489. Якою повинна бути мінімальна ширина дифракційної решітки, за допомогою якої можна розділити дві лінії спектра ртуті з довжинами хвиль l1 = 313,184 нм та l2 = 313,156 нм, якщо стала решітки 3,1 мкм?
Відповідь: 0,35 см.
490. На грань кристала кам’яної солі падає паралельний пучок рентгенівських променів. Відстань між атомними площинами кристала d =280пм. Під кутом q = 65° до площини грані спостерігається дифракційний максимум першого порядку. Визначити довжину хвилі рентгенівських променів.
Відповідь: 0,507 нм.
491. На грань кристала кам’яної солі падає вузький пучок рентгенівських променів (l = 0,15 нм). Під яким кутом до поверхні кристала повинні падати промені, щоб спостерігався дифракційний максимум першого порядку? Відстань між атомними площинами кристала дорівнює 0,285 нм.
Відповідь: 15,26°.
492. Паралельний пучок рентгенівських променів, яким відповідає довжина хвилі 0,15 нм, падає на поверхню кам’яної солі. Визначити відстань між атомними площинами кристала, якщо дифракційний максимум другого порядку спостерігається при куті ковзання падаючих променів в 30°.
Відповідь: 0,3 нм.
493. Падаючий на алюмінієву пластинку електронний промінь утворює при відбиванні дифракційний максимум другого порядку, який відповідає куту ковзання 84,55°. визначити швидкість електронів в промені, якщо відстань між атомними площинами кристалічної решітки алюмінію 0,4 нм.
Відповідь: 1,83×106 м/с.
494. Граничний кут повного внутрішнього відбивання для деякої речовини a = 45°. Знайти для цієї речовини кут повної поляризації.
Відповідь: 54,7°.
495. У скількох разів зменшується інтенсивність природного світла, яке пройшло крізь два поляризатори, площини поляризації яких складають кут 60o, якщо втрати інтенсивності поляризованого променя на поглинання в кожному поляроїді складають 10%?
Відповідь: І0/І = 9,87 рази.
496. Інтенсивність світла, що вийшло з аналізатора, дорівнює 10% інтенсивності природного світла, яке падає на поляризатор. Знайти кут між головними площинами поляризатора й аналізатора, якщо втрати інтенсивності поляризованого променя на поглинання в кожному поляроїді складають 8%.
Відповідь: φ =62,2о.
497. Аналізатор у 2 рази зменшує інтенсивність світла, що приходить до нього від поляризатора. Визначити кут між площинами поляризатора й аналізатора. Втрати інтенсивності світла в аналізаторі складають 10%.
Відповідь: φ =41,8о.
498. Природне світло падає на систему з трьох послідовно розташованих поляроїдів, причому головний напрямок середнього поляроїда складає кут φ = 60o з головним напрямком двох інших поляроїдів. Кожен поляроїд поглинає 19% падаючої на нього інтенсивності поляризованого світла. В скільки разів зменшиться інтенсивність світла після проходження цієї системи?
Відповідь: І0/І = 60,37 рази.
499. Чому дорівнює кут між головними площинами поляризації поляризатора й аналізатора, якщо інтенсивність природного світла, яке пройшло через поляризатор і аналізатор, зменшилася у 4 рази? Поглинанням світла знехтувати.
Відповідь: І0/І2 = 4.
500. Кут між площинами поляризації двох поляризаторів 60o. Природне світло, проходячи через таку систему, ослабляється в 10 разів. Знехтувавши втратами світла на відбивання, визначити коефіцієнт поглинання світла в поляроїдах.
Відповідь: ρ = 0,37
501. Чому дорівнює кут α між головними площинами поляризатора й аналізатора, якщо інтенсивність природного світла, що пройшло через аналізатор і поляризатор, зменшується у 4 рази? Коефіцієнт поглинання світла в кожному поляроїді дорівнює k = 10%.
Відповідь: φ = 38,2о.
502. Плоскополяризоване світло з інтенсивністю Io = 100 Вт/м² послідовно проходить через два поляризатори, площини поляризації яких утворять із площиною коливань у вхідному промені кути α1 = 20o і α2 = 50o (кути відраховуються від площини коливань по годинній стрілці, якщо дивитися уздовж променя). Визначити інтенсивність світла I на виході з другого поляризатора. Втратами інтенсивності світла в поляризаторах знехтувати.
Відповідь: І = 66 Вт/м2.
503. Пучок природного світла падає на систему із 4 ніколів, площини пропускання кожного з яких повернені на кут 30o відносно площини пропускання попереднього ніколя. Яка частина світлового потоку проходить через цю систему? Втратами інтенсивності світла в ніколях знехтувати.
Відповідь: І4/І0 = 0,21.
504. Пучок природного світла падає на систему із 6 поляроїдів, площини пропускання кожного з яких повернені на кут 60o відносно площини пропускання попереднього поляроїда. Яка частина світлового потоку проходить через цю систему? Втратами інтенсивності світла в поляроїдах знехтувати.
Відповідь: І6/І0 = 0,00049.
505. Знайти показник заломлювання n скла, якщо при відбиванні від нього світла відбитий промінь буде повністю поляризований при куті заломлювання b = 30°.
Відповідь: 1,73.
506. Під яким кутом q до горизонту повинно знаходитись Сонце, щоб його промені, відбиті від поверхні озера, були максимально поляризовані?
Відповідь: q = 37°.
507. Промінь плоскополяризованого світла (l =589 нм) падає на пластинку ісландського шпату перпендикулярно до його оптичної oсі. Знайти довжини хвиль lо та lе звичайного та незвичайного променів в кристалі, якщо показники заломлювання ісландського шпату для звичайного і незвичайного променів відповідно n0 = 1,66 та nе = 1,49.
Відповідь: l0 = 355 нм; lе = 395 нм.
508. Знайти кут між головними площинами поляризатора та аналізатора, якщо інтенсивність природного світла, яке проходить через поляризатор та аналізатор, зменшилась в чотири рази. Відбиванням та поглинанням світла знехтувати.
Відповідь: 45°.
509. У скільки разів зменшиться інтенсивність природного світла яке пройшло через два ніколі, площини поляризації яких складають кут 60°. Кожен ніколь відбиває та поглинає 10% падаючої на нього інтенсивності.
Відповідь: 9,91.
510. Осі двох поляроїдів розташовані під прямим кутом, а вісь третього поляроїда, розміщеного між ними, складає 30° з віссю першого. В скільки разів зменшиться інтенсивність світла, яке пройде через такий пристрій, якщо при проходженні кожного із поляроїдів на відбивання і поглинання втрачається 5% інтенсивності?
Відповідь: 12,5.
511. У досліді з двома ніколями втрати світла в поляризаторі та аналізаторі відповідно дорівнюють 8% та 10%. Кут між головними площинами поляризації ніколів дорівнює 30°. В скільки разів зменшилась інтенсивність світла після проходження поляризатора? після проходження аналізатора?
Відповідь: 2,2; 9,7.
512. На ніколь направлено природний промінь світла. При проходженні ніколя світло за рахунок поглинання і відбивання втрачає 8% енергії. Яким буде послаблення (у відсотках) незвичайного променя і чому?
Відповідь: 46%.
513. Розчин глюкози з концентрацією 2,8×102 кг/м3 , налитий в скляну трубку, повертає площину поляризації на кут 64°. Другий розчин, налитий в ту ж саму трубку, повертає площину поляризації на 48°. Знайти концентрацію другого розчину.
Відповідь: 2.1 × 102 кг/м3.
514. Розчин цукру з концентрацією 25×102 кг/м3 товщиною 20 см повертає площину поляризації монохроматичного світла на кут 33,3°. Інший розчин товщиною 15 см повертає площину поляризації на кут 20°. Визначити концентрацію цукру в другому розчині.
Відповідь: 1,55 × 102 кг/м3.
515. Розміщений між двома поляризаторами розчин цукру в трубці довжиною 18 см повертає площину поляризації жовтих променів полум’я натрію на 30°. Яка маса цукру в 1 м3 розчину, якщо питоме повертання площини поляризації цукру для жовтих променів натрію 0,667 о/м2×кг.
Відповідь: 250 кг.
516. Концентрація налитого в скляну трубку розчину цукру дорівнює 0,3г/см3. Цей розчин повертає площину поляризації монохроматичного світла на 25°. Визначити концентрацію іншого розчину цукру, налитого в коротшу в два рази трубку, якщо він повертає площину поляризації на 2,5°.
Відповідь: 0,06 г/см3.
517. Між схрещеними ніколями поляризатора розмістили трубку з цукровим розчином. Поле зору при цьому стало максимально світлим. Визначити довжину трубки, якщо концентрація цукру 270 кг/м3, а його питоме повертання 0,665о/кг.м2.
Відповідь: 50 см.
518. Визначити найменшу товщину пластинки у півхвилі, виготовленої з ісландського шпату, для світла з довжиною хвилі 687 нм, якщо показники заломлювання звичайного та незвичайного променів цього світла відповідно дорівнюють 1,653 та 1,484.
Відповідь: 2×10-4 см.
519. Зелене світло було максимально послаблене при проходженні через два схрещених ніколі. Якої товщини пластинку з кварцу потрібно помістити між ніколями, щоб поле зору стало максимально світлим. Питоме повертання кварцу для зеленого світла дорівнює 463 рад/м?
Відповідь: 3,4 мм.
520. Між схрещеними ніколями розмістили кварцову пластинку, вирізану паралельно до оптичної осі. Для одержання повного затемнення поля зору, аналізатор повернули на кут 20°. Визначити товщину пластинки, якщо дослід проводився з монохроматичним світлом, для якого стала повертання площини поляризації кварцу дорівнює 29,7° на 1 мм.
Відповідь: 0,67 мм.
521. Визначити найменшу товщину кварцової пластинки в четверть хвилі для світла з довжиною хвилі 527 нм. Показники заломлювання звичайного і незвичайного променів в пластинці відповідно дорівнюють 1,547 та 1.537.
Відповідь: 0,026 мм.
522. Якою має бути напруженість електричного поля в приладі Керра з сірководнем (стала Керра для сірководню 3,89×10-14 м/В), щоб зсув фаз при довжині пластин конденсатора 5 см дорівнював p /2? Довжина хвилі світла, яке взято для досліду - 5×10-7 м.
Відповідь: 8 кВ/м.
523. Показники заломлювання води при 20° С для світла з довжинами хвиль 670,8, 656,3 та 643,8 нм відповідно рівні 1,3308, 1,3311 та 1,3314. Визначити фазову та групову швидкості світла біля довжини хвилі 656,3 нм.
Відповідь: υ = 2,25×108 м/с; u = 2,23×108 м/с.
524. Показники заломлювання води при 20° С для світла з довжинами хвилі 508,6; 486,1 та 480,0 відповідно дорівнюють 1,3360; 1,3371 та 1,3374. Визначити фазову та групову швидкості біля довжини хвилі 486,1 нм.
Відповідь: 2,24×108 м/с; u = 2,20×108 м/с.
525. Показники заломлювання води при 20° С для світла з довжинами хвиль 589,3; 546,1 та 508,6 нм відповідно дорівнюють 1,3330; 1,3345; 1,3360. Визначити співвідношення фазової та групової швидкості світла біля довжини хвилі 546,1 нм.
Відповідь: 1,0155.
526. Показник заломлювання води для світла з довжиною хвилі в вакуумі 760 нм дорівнює 1,239, а для світла з довжиною хвилі 400 нм – 1,344. На скільки відсотків відрізняються фазові швидкості світла в воді?
Відповідь: 1,13%.
527. Чому дорівнює фазова швидкість світла в воді, якщо при частоті 4,4×1014 Гц довжина хвилі дорівнює 510 нм?
Відповідь: 2,24×104 м/с.
528. Показники заломлювання флюориту для світла з довжиною хвиль 670,8; 656,3; 643,8; 643,8 нм відповідно дорівнюють 1,4323; 1,4325; 1,4327. Обчислити відношення фазової швидкості до групової біля довжини хвилі 656,3 нм.
Відповідь: 1,0048.
529. Визначити відносне зменшення інтенсивності світла при проходженні ним віконного скла, товщиною 4 мм за рахунок поглинання. Коефіцієнт поглинання скла 1,23м-1.
Відповідь: 0.5%.
530. Коефіцієнт лінійного поглинання речовини дорівнює 2,5×10-3 с-1. Визначити товщину шару цієї речовини, яка послаблює інтенсивність монохроматичного світла в 5 разів.
Відповідь: 6,44 м.
531. Якої товщини шар речовини послаблює інтенсивність монохроматичного світла в 2 рази, якщо коефіцієнт поглинання речовини дорівнює 1,38 м-1?
Відповідь: 0,502 м.
532. Визначити коефіцієнт поглинання червоного світла в воді, якщо товщина шару половинного послаблення дорівнює 30 см.
Відповідь: 2,31 1/м.
533. Як зміниться інтенсивність монохроматичного світла при проходженні через два шари поглинача: товщина першого шару 10-2 м, другого 2×10-2 м, коефіцієнти лінійного поглинання відповідно дорівнюють 0,1 та 0,3 см-1 .
Відповідь: зменшиться в 2,014 разу.
534. Два захисних шари деяких речовин однакової товщини послаблюють інтенсивність монохроматичного світла: перший в 2 рази при коефіцієнті поглинання 5 м-1, другий - в 5 разів. Визначити коефіцієнт поглинання другого шару.
Відповідь: 11,61 м-1.
535. Визначити довжину шару деякого металу з коефіцієнтом поглинання 106 м-1, який послаблює інтенсивність світла в е разів.
Відповідь: 10-6 м.
536. Площа поверхні вольфрамової нитки розжарювання 25-ватної лампочки дорівнює 0,403 см2, а її температура розжарювання 2450 К. У скільки разів випромінюється енергії лампочкою менше, ніж абсолютно чорним тілом за тих же умов?
Відповідь: 0,3.
537. Потік енергії, випромінюваної з оглядового віконця плавильної печі 34 Вт. Визначити температуру печі, якщо площа отвору - 6 см².
Відповідь: Т = 1000 К.
538. Температура верхніх шарів зірки Сіріус дорівнює 104 К. Визначити потік енергії, випромінюваної з поверхні площею 1 км² цієї зірки.
Відповідь: N = 56,7.1015 Вт.
539. Приймаючи коефіцієнт чорноти вугілля при температурі 600o рівним 0,8, визначити енергію, яка випромінюється з поверхні в 5 см² нагрітого вугілля за 10 хвилин.
Відповідь: 1763,6 Дж.
540. Потужність випромінювання кулі радіусом 10 см при деякій постійній температурі дорівнює 1000 Вт. Знайти цю температуру, якщо коефіцієнт чорноти кулі дорівнює 0,25.
Відповідь: 865,7 К.
541. Знайти температуру печі, якщо відомо, що з отвору в ній площею 6,0 см2 випромінюється за 1 секунду 34,02 Дж енергії. Випромінювання вважати близьким до випромінювання абсолютно чорного тіла.
Відповідь: Т=1000 К.
542. Температура вольфрамової спіралі в 25-ватної електричної лампочки дорівнює 2450 К. Приймаючи коефіцієнт чорноти рівним 0,3, знайти величину площі випромінюючої поверхні спирали.
Відповідь: S = 0,4 см2.
543. Діаметр нитки вольфрамової спіралі в електричній лампочці дорівнює 0,3 мм, довжина нитки спіралі 5 см. При вминанні лампочки в ланцюг з напругою 127 В через лампочку тече струм силою 0,31 А. Знайти температуру нагрівання спіралі, при умові, що після встановлення рівноваги вся теплова енергія випромінюється циліндричною поверхнею нитки спіралі. Коефіцієнт чорноти дорівнює 0,31.
Відповідь: Т= 3714 К.
544. З поверхні нагрітої сажі площею 2 см² при температурі 400 К за час 5 хв. випромінюється 83 Дж енергії. Визначити коефіцієнт чорноти сажі.
Відповідь: α = 0,95.
545. Визначити температуру поверхні Сонця, приймаючи її за абсолютно чорне тіло, якщо відомо, що максимум інтенсивності спектра Сонця лежить у зеленій області λm = 5·10-7 м. Яка його енергетична світність?
Відповідь: Т = 5800 К; Re = 6,4.107 Вт/м2.
546. Поверхня Сонця близька за своєю властивістю до абсолютно чорного тіла. Максимум випромінювальної здатності цієї поверхні приходиться на довжину хвилі λm = 0,50 мкм. Визначити температуру сонячної поверхні й енергію W, яку випромінює Сонце за τ = 1 с у вигляді електромагнітних хвиль. Радіус Сонця 6,95·108 м.
Відповідь: W = 3,89.1026 Дж.
547. Визначити температуру плавильної печі, якщо відомо, що з її віконця площею поверхні 6 см2 щосекунди випромінюється 168 Дж променистої енергії.
Відповідь: 1650 К.
548. Потік випромінювання абсолютно чорного тіла Ф = 10 кВт, максимум енергії випромінювання приходиться на довжину хвилі l = 0,8 мкм. Знайти площу поверхні випромінювання.
Відповідь: 10-3 м2.
549. У скільки разів зросте потужність випромінювання абсолютно чорного тіла, якщо максимум енергії в його спектрі переміститься з довжини хвилі 0,6 мкм до 0,5
