Блок сохранения данных в рабочей области То Workspace

Назначение: Блок записывает данные, поступающие на его вход, в рабочую область MATLAB.

Параметры:

Variable name – имя переменной, содержащей записываемые данные.

Limit data points to last – максимальное количество сохраняемых расчетных точек по времени (отсчет ведется от момента завершения моделирования). В том случае, если значение параметра Limit data points to last задано как inf, то в рабочей области будут сохранены все данные.

Decimation – кратность записи данных в рабочую область.

Sample time – шаг модельного времени. Определяет дискретность записи данных.

Save format – формат сохранения данных. Может принимать значения:

1. Matrix – матрица. Данные сохраняются как массив, в котором число строк определяется числом расчетных точек по времени, а число столбцов – размерностью вектора подаваемого на вход блока. Если на вход подается скалярный сигнал, то матрица будет содержать лишь один столбец.

2. Structure – структура. Данные сохраняются в виде структуры, имеющей три поля: time – время, signals – сохраняемые значения сигналов, blockName – имя модели и блока To Workspace. Поле time для данного формата остается не заполненным.

3. Structure with Time – структура с дополнительным полем (время). Для данного формата, в отличие от предыдущего, поле time заполняется значениями времени.

На рис. 6.13 показан пример использования данного блока. Результаты расчета сохраняются в переменной simout.

Для считывания данных сохраненных в рабочей области MATLAB можно использовать блок From Workspace (библиотека Sources).

 

Рис. 6.13 – Применение блока To Workspace

Блок ScopeNew

Назначение: Строит графики исследуемых сигналов в функции времени на белом фоне. Преимущество перед блоком Scope в том, что есть возможность копировать графики на белом фоне.

ЛЕКЦИЯ №7

ОСНОВЫ ПРЕДСТАВЛЕНИЯ МОДЕЛЕЙ «ВХОД – ВЫХОД» ЛИНЕЙНЫХ ЗВЕНЬЕВ И СИСТЕМ В ИНЖЕНЕРНОЙ ПРАКТИКЕ

 

Линеаризация моделей

Внимание! При дальнейшем изложении материала будет использоваться такое понятие, как динамическое звено. Звено, представляет собой удобное математическое образование (виртуальное), которое описывается дифференциальным уравнением и представляется в виде прямоугольника со входами и выходами (вспомните, структурную схему объекта). Уравнение звена выражает зависимость между входными и выходными величинами данного звена. Динамическое уравнение звена (математическая модель звена) составляется по правилам соответствующей технической науки (звено может представлять собой тепловой двигатель, электрическую машину, механическую передачу, электрическую цепь и т.д.).

Вспомним, что принципиальным требованием к моделям объектов является отражение динамики во взаимосвязи между входными и выходными переменными. Поэтому входные и выходные переменные рассматриваются как процессы (их мы уже научились моделировать на компьютере). А модели преобразования воздействий, т.е. связь между входными и выходными переменными, математически должны описываться дифференциальными уравнениями.

Модель должна отражать существенные для исследователя свойства объекта. С одной стороны, модель должна как можно лучше отражать свойства реального объекта или системы, т.е. быть достаточно сложной. С другой стороны, она должна быть достаточно простой, чтоб ее составление занимало приемлемое время. Поэтому обычно стремятся к упрощениям при получении моделей.

Все модели реальных систем – нелинейные, так как всегда существует предельно допустимое значение входного сигнала и при его превышении объект может просто выйти из строя или даже разрушиться. Методы исследования нелинейных систем очень сложны математически.

Поэтому главным упрощением, к которому стремятся, является линеаризация моделей – использование для описания свойств объектов линейных дифференциальных уравнений.

Линеаризация допустима в следующих случаях:

1) аргумент линеаризуемой функции и сама функция изменяются на ограниченных интервалах;

2) нелинейная функция является гладкой (без разрывов) и монотонной (возрастающая или убывающая).

Идея линеаризации заключается в том, что в системах регулирования (поддержания заданных значений) сигналы мало отклоняются от рабочей точки – некоторого положения равновесия, в котором все сигналы имеют нужные значения и их производные равны нулю.

В общем случае процесс линеаризации связан с разложением нелинейной функции в ряд Тейлора в окрестности некоторой внутренней точки интервала изменения переменной и последующим отбрасыванием всех членов ряда со степенью превышающей единицу.

Рассмотрим линеаризацию на простом примере. Пусть дано звено, у которого взаимосвязь в статически установившихся режимах между входной (х) и выходной (у) переменными нелинейна, т.е. имеющее нелинейную статическую характеристику q(x). Используя понятие математической модели типа «вход-выход», изобразим его структурную схему (рис. 7.1):

 

 

Рис. 7.1

 

Пусть также входная (аргумент) и выходная (функция) переменные этого звена изменяются в некоторой окрестности точки С (х₀, у₀), заданной интервалами х Î [x₁, x₂], y Î [y₁, y₂], см. рис. 7.2.

 

 

 

Рис. 7.2

 

Раскладывая исходную нелинейную зависимость q(x) в окрестности точки C(x₀, y₀) в ряд Тейлора, и отбрасывая нелинейные члены, получим следующую зависимость (7.1):

, (7.1)

которая представляет собой аналитическое выражение линеаризованной статической характеристики звена по каналу «х – у», т.е. статической характеристики линейной модели звена по этому каналу.

Значение частной производной при значении х = х₀, k = называется коэффициентом передачи звена.

 

Графическая интерпретация процедуры линеаризации: В точке С(х₀, у₀) проводим касательную к кривой у = q(x) (ее угловой коэффициент tg(a) = k). На отрезке [х₁, х₂] кривая у = q(x) заменяется прямой y = y₀ + k(x – x₀), которая и представляет собой линеаризованную статическую характеристику звена.

Преобразуем выражение для статической характеристики звена от формы, когда мы оперируем с абсолютными значениями переменных, к форме, когда переменные задаются в приращениях относительно координат точки С. Для этого преобразуем выражение (7.1) к виду: у – у₀ = k(x – x₀). Обозначим: у – у₀ = Dу, а х – х₀ = Dх. Получаем линеаризованное уравнение звена в приращениях (отклонениях) от точки С: Dу = kDх.

Замечание: линеаризованная характеристика может быть корректно использована только на интервале линеаризации (изменение аргумента на отрезке от х₁ до х₂).

Примеры функций, для которых рассмотренная процедура линеаризации характеристик недопустима, см. рис. 7.3 и 7.4:

 

 

Рис. 7.3 Рис. 7.4

Передаточная функция

Дифференциальное уравнение звена (системы) в общем виде можно представить в виде:

. (7.2)

После перевода уравнения (7.2) к переменным в отклонениях и его линеаризации, уравнение принимает вид (8.3):

+ + + … + +

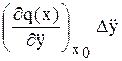+ + + … = 0, (7.3)

где обозначает, что для частной производной вычислено ее значение в точке С(х₀, у₀).

 

Возвращаясь к структурной схеме модели звена типа «вход – выход», изменим ее с учетом появившихся обозначений:

 

 

В теории систем автоматического управления приняты определенные формы записи дифференциальных уравнений, придающие их коэффициентам определенный физический смысл. Рассмотрим это на примере уравнения (7.3), считая его второго порядка. Осуществим следующие действия:

1) выходную переменную Dу оставим в левой части, а входную переменную Dх перенесем в правую часть уравнения:

+ + =

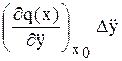+ + ; (7.4)

2) разделим обе части уравнения на коэффициент перед приращением выходной величины Dу:

Dу + + =

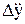= Dх + +

+ ; (7.5)

3) обозначим полученные коэффициенты перед переменными символами, отражающими их физический смысл и размерность:

. (7.6)

Для лучшего понимания рассмотрим, как были получены коэффициенты k и Т₂, их размерность и общепринятые названия:

коэффициент передачи

k = –; (7.7)

= = [c²] (7.8)

– постоянная времени. (7.9)

Перепишем (7.6) в развернутом виде:

. (7.10)

Введем оператор дифференцирования , который действует на сигнал по правилу . Здесь важно, что запись обозначает не умножение оператора на сигнал, а действие этого оператора, то есть дифференцирование .

(7.11)

или . (7.12)

Используемые в данном уравнении коэффициенты приводят все слагаемые уравнения к одной размерности – размерности выходной переменной.

Замечание: в дальнейшем будем рассматривать дифференциальные уравнения только в отклонениях. Поэтому, для сокращения записи символ «D» использовать не будем.

С учетом данного замечания перепишем уравнение (7.12):

, (7.13)

В компактной форме: Q(p)y(t) = R(p)x(t), y(t) = . (7.14)

Полученное выражение является символической записью уравнения (7.4), которой удобно пользоваться. И запись (7.14) означает не умножение, а действие сложного оператора на сигнал .

Функция обозначается и называется передаточной функцией. Она полностью описывает связи между входом и выходом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.

Преобразование Лапласа

При управлении объектами важно уметь вычислять выходной сигнал системы при известном входном. Для решения такой задачи необходимо решать ДУ. Чтоб упростить процедуру, существует специальное преобразование, которое позволяет заменить решение ДУ алгебраическими вычислениями.

Для функции вводится преобразование Лапласа, которое обозначается как .

(7.15)

Функция F(s) называется изображением для функции f(t) (оригинала). Здесь s – это комплексная переменная, которая выбирается так, чтобы интеграл (7.15) сходился.

Обратное преобразование Лапласа позволяет вычислить оригинал f(t) по известному изображению F(s).

(7.16)

Где , а постоянная выбирается так, чтобы интеграл сходился.

На практике вместо интеграла чаще всего используют готовые таблицы, по которым можно сразу определить изображение по оригиналу и наоборот.

Например, изображение Лапласа для единичного ступенчатого сигнала

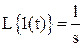
А изображение Лапласа для экспоненциального сигнала имеет вид:

Свойства преобразования Лапласа:

1. Выполнение принципа суперпозиции как для прямого так и для обратного преобразования Лапласа:

2. Изображение для производной функции равно:

,

где F(s) – изображение функции f(t), и f(0) – ее значение при t=0.

Поэтому при нулевых начальных условиях изображение производной равно изображению функции умноженному на s. А для построения изображения i-той производной нужно умножить изображение функции на .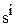

Иногда используют передаточную функцию как отношение изображений по Лапласу входного и выходного сигналов звена и обозначают: .

Здесь важно, что переход от одного вида передаточной функции к другому осуществляется формальной заменой pна sпри нулевых начальных условиях.