Вычислять вероятности случайных событий по определению вероятности события бывает порой довольно затруднительно. Поэтому для вычисления вероятностей пользуются правилами, позволяющими по известным вероятностям одних событий вычислять вероятности других событий, получаемых из них с помощью некоторых операций. Дадим определения этим операциям.
Cуммой событий А и В называется событие С, которое состоит в том, что происходит хотя бы одно из данных событий. Обозначение суммы: 
.
Произведением событий А и В называют событие С, состоящее в том, что происходят оба события А и В. Обозначение: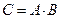 
.
Событием, противоположным событию А называют событие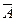 
, которое состоит в том, что А не происходит, то есть если А не происходит, то происходит .
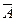Теперь укажем формулы, по которым можно вычислять вероятности определенных выше событий.
1. 
), если события 
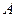и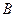 
совместны;
2. 
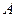, если события и 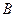несовместны
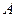События и 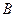называются независимыми, если появление одного из них не меняет вероятности появления другого. В противном случае события называются зависимыми.
Число, выражающее вероятность событи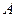я при условии, что произошло событие 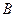, называется условной вероятностью событи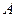я относительно 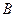и обозначается символом 
.
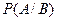Событи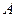я и 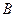независимы, если 
.
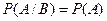3. 
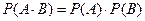для независимых событий,
4. 
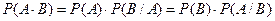для зависимых событий.
5. Если событи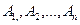я 
независимы в совокупности (то есть для любого подмножества этих событий вероятность их произведения равна произведению вероятностей), то вероятность наступления хотя бы одного из этих событий вычисляется по формуле:
.
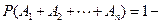
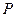
Задачи
21. Монета подбрасывается три раза. Событие Аi – появление герба при i-том исходе. Представить с помощью операций сложения и умножения событий Аi и 
следующие события:
а) А – все три раза выпадет герб,
б) В – все три раза появится цифра,
в) С – хотя бы один раз появится герб,
г) D – в точности один раз появится цифра,
д) Е – не менее двух раз выпадет герб,
е) F – герб выпадет не раньше третьего раза.
22. Бросили медную и серебряную монеты и рассмотрели события:
А – герб выпал на медной монете,
В – цифра выпала на медной монете,
С – герб выпал на серебряной монете,
D – цифра выпала на серебряной монете,
М – выпал хотя бы один герб,
F – выпала хотя бы одна цифра,
G – выпал один герб и одна цифра,
H – герб не выпал ни одного раза,
K – выпало два герба.
Каким событиям из этого списка равны события: 1) 
; 2) 
; 3) MÇF; 4) GÈM; 5) GÈM; 6) ВÇ D; 7) МÈК.
23. По мишени производится три выстрела.Рассматриваютс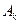я события 
- «попадание при 
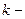ом выстреле», 
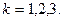Пользуясь операциями над событиям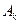и , запишите формулы следующих событий:
А – все три попадания,
В – все три промаха,
С – хотя бы одно попадание,
D – хотя бы один промах,
М – не менее двух попаданий,
F – не более одного попадания,
G – попадание в мишень не раньше третьего выстрела,
H – ровно одно попадание,
K – ровно два попадания.
24. Стрелок стреляет по мишени, разделенной на три области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35. Найдите вероятность того, что стрелок попадет в первую или во вторую область.
25. В мастерской работают три станка. За смену первый станок может потребовать наладки с вероятностью 0,15. Для второго станка эта вероятность равна 0,1, а для третьего станка – 0,12. Найдите вероятность того, что за смену хотя бы один станок потребует наладки, считая, что одновременно станки наладки потребовать не могут.
26. В цехе работает несколько станков. Вероятность того, что за смену потребует наладки ровно один станок, равна 0,2. Вероятность того, что за смену потребуют наладки ровно два станка – 0,13, больше двух станков – 0,07. Какова вероятность того, что за смену придется проводить наладку станков.
27. Бросаются две игральных кости. Какова вероятность того, что выпала хотя бы одна шестерка.
28. В ходе задержания преступника было применено огнестрельное оружие. Вероятность попадания в жизненно важные органы равна 0,3, в остальные части тела – 0,2. Найдите вероятность того, что преступник ранен в результате одного выстрела.
29. Подбрасываются две монеты. Рассматриваются: событие А – появление цифры на первой монете, событие В – появление цифры на второй монете. Найдите вероятность события С = А + В.
30. Берется наудачу трехзначное число. Какова вероятность того, что хотя бы две его цифры совпадают?.
31. Вероятность того, что студент Синицын сдаст экзамен по предмету А равна 0,9, а вероятность успешной сдачи экзамена по предмету В для него равна 0,7. Какова вероятность того, что он успешно сдаст оба экзамена?
32. В первом ящике 5 белых и 10 черных шаров. Во втором ящике 12 белых и 4 черных шара. Из каждого ящика вынули по шару. Какова вероятность того, что 1)оба шара белые? 2)один из вынутых шаров черный, а другой белый?
33. По делу о краже в суде находятся три свидетеля. Вероятность того, что первый свидетель дает ложные показания равна 0,3, для второго вероятность дачи ложных показаний равна 0,5, а для третьего – 0,4. Какова вероятность того, что а) все три свидетеля говорят правду? б) правду говорит в точности один из них? в) по крайней мере, один из них говорит правду?
34. Подбрасывают три монеты. Найдите вероятность того, что герб выпадет на всех трех монетах.
35. Игральный кубик подброшен 3 раза. Найдите вероятность того, что все три раза выпадет два очка.
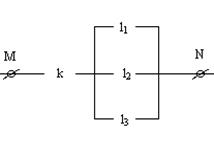36. Электрическая цепь между точками M и N составлена по схеме, приведенной на рисунке. Выход из строя за время Т различных элементов цепи – независимые события. Вероятность выхода из строя элемента k равна 0,6, элемента l1 равна 0,4, элемента l2 – 0,7, l3 – 0,9. Определите вероятность разрыва цепи за указанный промежуток времени.
Решение.
Обозначим через А событие, состоящее в выходе из строя элемента k, а через В – выход из строя всех трех элементов li (i = 1, 2, 3). Тогда искомая вероятность
.
Так как Р(А) = 0,6, а 
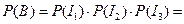0,4 × 0, 7 × 0, 9 = 0,252,
то 
0,6 + 0,252 - 0,6 × 0,252 = 0,852 - 0,1512 = 0,7008.
Ответ. 0,7008.
37. Студент изучает гражданское право, английский язык и уголовное право. Он оценивает, что вероятность получить «отлично» по этим курсам равна соответственно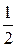 
, 
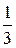и 
. В предположении, что оценки студента по трем дисциплинам независимы, найдите вероятность того, что, что 1) он не получит ни одной «пятерки»; 2) получит «пятерку» только по гражданскому праву.
38. В копилке осталосьшесть монет: четыре по 10 копеек и две по 50 копеек. Из нее извлекают последовательно одна за другой две монеты. Какова вероятность, что извлеченные монеты будут 1) одного достоинства? 2) разных достоинств?
39. Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Определите вероятность того, что в цель попадет хотя бы один стрелок.
Решение.
1 способ. Пусть событие А состоит в том, что первый стрелок попадет в цель, В – что второй попадет в цель, С – в цель попадет третий, D – в цель попадет хотя бы один. Тогда D = А + В + С.
(
) = 1- Р() × Р() × Р()=
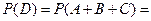
= 1 - (1 - 0,75)×(1 - 0,8)×(1 - 0,9) = 1 - 0,005 = 0,995.
2 способ. Применим правило сложения вероятностей:
.
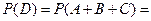
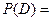0,75 + 0,8 + 0,9 - 0,6 - 0,675 - 0,72 + 0,54 = 0,995.
40. Для охраны организацией в офисе были установлены два сигнализатора, работающих независимо друг от друга. Вероятность тог, что при незаконном проникновении в помещении сигнализатор сработает, равна 0,85 для первого сигнализатора и 0,92 для второго. Найдите вероятность того, что при незаконном проникновении сработает 1)только один сигнализатор; 2) хотя бы один сигнализатор.
41. Вероятность того, что студент сдаст первый экзамен, равна 0,9, вероятность того, что он сдаст второй экзамен, равна 0,6, третий – 0,7. Найдите вероятность того, что
1) он сдаст хотя бы один экзамен;
2) он сдаст только 2 экзамена;
3) он сдаст не более двух экзаменов;
4) он сдаст более двух экзаменов;
5) он сдаст только один экзамен.
42. Вероятности появления каждого из двух независимых событий А1 и А2 равны соответственно р1 и р2. Найдите вероятность появления только одного из этих событий.
43. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,75, для третьего – 0,7. Какова вероятность:
1) хотя бы одного попадания,
2) ровно одного попадания,
3) ровно двух попаданий,
4) трех попаданий, если каждый сделал по одному выстрелу?
5)Какова вероятность того, что все промахнулись?
44. Трем студентам нужно решить по задаче в течение получаса. Вероятности того, что студенты выполнят свое задание в срок, составляют соответственно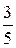 
, 
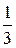и . Какова вероятность того, что через полчаса все три студента решат свои задачи? Что задачи решат только двое студентов?
45. В первом ящике лежат а белых и b черных шаров. Во втором ящике – c белых и d черных шаров. Из каждого ящика вынули по шару. Какова вероятность, что оба шара черные?
46. Из 36 карт наугад выбирают две карты одну за другой, без возвращения в колоду первой вынутой карты. Какова вероятность того, что
а) будут вынуты два туза?
б) первой вынутой картой окажется дама крестей?
в) не будет вынут ни один туз?
г) будут вынуты шестерка и валет крестей?
д) второй картой окажется туз пик?
Решите эту же задачу для случая, когда первая выбранная карта возвращается в колоду перед тем, как выбирается вторая карта.
47. В ящике имеются 7 белых, 8 черных и 5 красных шаров одного размера. Наугад вынимаются подряд два шара. Какова вероятность того, что: а) будут вынуты два черных шара? б) будут вынуты белый и черный шары? в) будут вынуты шары одного цвета? г) второй шар окажется белым? д) первый шар окажется красным?
48. Из карточек составлено слово «следователь». Из них выбирают наугад поочередно 4 карточки и приставляют одну к другой (в том порядке. как выбирали). Какова вероятность того, что получится слово 1)«дело» 2) «след» 3) «сель» 4) «тело» 5) «свет»?
49. Определите вероятность того, что на вырванном наудачу листке нового календаря (365 дней) окажется а) четное число, б) число 10, в) нечетное число?
50. Вероятность того, что подсудимого признают виновным по первой статье, равна 0,6, а по второй – 0, 3. Найдите вероятность того, что подсудимого признают виновным хотя бы по одной статье; только по одной статье.
51. Бросили игральную кость. Найдите вероятность того, что выпало простое число очков, при условии, что число выпавших очков нечетно.
52. В ящике лежат 12 красных, 8 зеленых и 10 синих шаров, одинаковых на ощупь. Наудачу вынимается один шар. Какова вероятность того, что он красный, если известно, что он не синий?
53. В ящике лежат 12 красных, 8 зеленых и 10 синих шаров, одинаковых на ощупь. Наудачу вынимаются два шара. Какова вероятность того, что: 1) они зеленые, если известно, что при этом не вынут синий шар; 2) вынутые шары разноцветные, если известно, не вынут синий шар?
54. Ведутся поиски четырех преступников. Каждый из них независимо от других может быть обнаружен в течении суток с вероятностью 0,5. Какова вероятность того, что в течении суток: а) будет обнаружен хотя бы один преступник? б) по крайней мере, два преступника? в)В точности два преступника? г) Все четыре преступника?
55. В группе10 студентов, среди которых 4 отличника. На занятии к доске вызывают 3 студентов. Найдите вероятность того, что среди них хотя бы один отличник.
56. Король Артур проводит рыцарский турнир, в котором порядок состязания определяется жребием. Среди восьми рыцарей, одинаково искушенных в ратном деле двое близнецов. Какова вероятность, что они встретятся в турнире?
5.3. Полная группа событий. Формула полной вероятности
Напомним, что события А1, А2, …, Аk образуют полную группу, если они попарно несовместны и их сумма является достоверным событием:
А1 + А2 + … + Аk = U.
Пусть события 
образуют полную группу, и событие А наступает только после наступления одного из этих событий, а какого именно, неизвестно. Тогда вероятность события А вычисляется по формуле
.
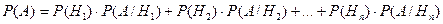Эта формула называется формулой полной вероятности, а события, , после одного из которых наступает событие А, – гипотезами.
Из формулы полной вероятности легко найти вероятност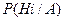ь 
для любого 
(
):
,
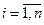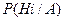
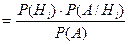где .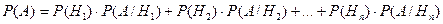
Эту формулу называют формулой Байеса.
Ее применяют при решении практических задач, связанных с вероятностной оценкой гипотез после проведения эксперимента, так как она позволяет найти вероятность каждой гипотезы при условии, что событие произошло.
Задачи
57. Поступающие в магазин часы изготовляются на трех заводах. Первый завод производит 40% продукции, второй – 45%, третий – 15%. В продукции первого завода 80% часов спешат, второго завода 70% часов спешат, третьего – 90% часов спешат. Какова вероятность того, что купленные наудачу часы спешат?
58. Детали на сборку поступают с трех автоматов, Известно, что первый автомат дает 0,3% брака, второй – 0,2%, третий – 0,4%. Найдите вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000 деталей, со второго – 2000, с третьего – 2500.
59. По самолету производятся три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,8. При одном попадании самолет сбивается с вероятностью 0,3, при двух – с вероятностью 0,6, а при трех самолет сбивается наверняка. Какова вероятность сбить самолет?
60. Два станка производят детали, поступающие на общий конвейер. Вероятность получения стандартной детали на первом станке равна 0,9, на втором – 0, 85. Производительность второго станка вдвое больше производительности первого. Определите вероятность того, что наудачу взятая с конвейера деталь стандартная.
61. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0, 02, для второго – 0,03, для третьего – 0, 04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше производительности второго, а третьего в два раза меньше, чем второго. Определите вероятность того, что взятая наудачу из ящика деталь будет бракованной.
62. В белом ящике лежат 12 красных и 6 синих шаров, одинаковых на ощупь. В желтом ящике лежат 15 красных и 10 синих одинаковых на ощупь шаров. Бросается игральная кость. Если число выпавших очков кратно трем, то наудачу вынимают шар из белого ящика. Если число выпавших очков не кратно трем, то наудачу вынимают шар из желтого ящика. Какова вероятность вынуть красный шар?
63. Старшая дочь моет посуду раз в неделю. Вероятность того, что она разобьет тарелку, составляет 5%. Младшая дочь моет посуду во все остальные дни. Вероятность того, что она разобьет тарелку, равна 20%. Какова вероятность того, что в среду во время мытья посуды будет разбита тарелка? Какова вероятность, что эту тарелку разбила младшая дочь?
64. Фирма продает батарейки, изготовленные на двух заводах. Первый завод поставляет на фирму 60% батареек, второй – 40%. Вероятность брак на первом заводе составляет 3%, на втором – 4%. Найдите вероятность того, что купленная на фирме батарейка окажется без брака. Найдите вероятность того. что эта батарейка изготовлена на первом заводе.
65. В двух пакетах находятся по 20 конфет одинаковой формы. В первом пакете 5 конфет с темной начинкой, а остальные – со светлой. Во втором – 8 конфет с темной начинкой, а остальные – со светлой. Из наудачу выбранного пакета берут одну конфету. Какова вероятность, что взята конфета с темной начинкой?
66. В магазине половина всех товаров произведена на первой фабрике, 1/3 всех товаров – на второй, 1/6 всех товаров – на третьей. Вероятность брака на первой фабрике составляет 0,04, на второй – 0,01, на третьей – 0,04. Куплено одно изделие. Какова вероятность, что оно бракованное? Какова вероятность, что купленное бракованное изделие изготовлено на третьей фабрике?
67. Первая секретарь-машинистка набрала 200 страниц текста и в 5% из них сделала ошибки. Вторая машинистка набрала 300 страниц и в 3% из них сделала ошибки. Наудачу для проверки выбрана одна страница текста. С какой вероятностью она содержит ошибки?
68. В первой урне 5 белых и 15 черных шаров, а во второй урне – 4 белых и 8 черных шаров. Из первой урны во вторую переложили один шар. Затем из второй урны вынули один шар. С какой вероятностью этот шар окажется белым? Черным?
69. В первой урне 20 шаров, среди которых 5 шаров – белые.Во второй урне 10 шаров, из них 3 белых. Из каждой урны взяли наудачу по одному шару, а затем из этих двух шаров выбрали наудачу один шар. С какой вероятностью он окажется белым?
70. На экзамене студенту предлагается выбрать наугад один из 20 экзаменационных билетов. Он может ответить на «отлично» на 8 билетов с вероятностью 0,9, еще на 10 билетов – с вероятностью 0,6 и на 2 билета – с вероятностью 0,2. Найдите вероятность того, что студент, выбрав билет, ответит на него на «отлично».
71. В ящик, содержащий 2 шара, опускают белый шар, после чего из него наудачу берут шар. Найдите вероятность того, что извлеченный шар белый, если все предположения о первоначальном составе шаров по цвету равновозможны.
72. В специализированнуюбольницу поступают в среднем 50% больных с заболеванием А, 30% больных с заболеванием Б, 20% – с заболеванием С. Вероятность полного излечения болезни А равна 0,7. Для болезней Б и С эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, выписан здоровым. Найдите вероятность того, что он страдал заболеванием А.
73. Преподаватель шутки ради предложил студенту распределить по двум урнам два белых и один черный шар. Преподаватель выбирает наугад урну и вынимает из нее один шар. Если шар будет белый, то студент получает зачет по теории вероятностей. Каким образом студенту следует распределить шары по урнам, чтобы иметь наибольший шанс получить зачет?
74. Имеются три колоды по 36 карт и две колоды по 52 карты. Наудачу выбирается колода, а из нее карта. 1) Какова вероятность, что взят туз? 2) Взятая карта оказалась дамой. Какова вероятность, что она взята из колоды в 36 карт?
Случайные величины
