Для звена 3 заменяем силу инерции 
и момент сил инерции 
одной силой 
, равной по величине и направлению силе , но приложенной в центре качания k3 звена. Для его нахождения вычисляем плечо
что в масштабе кинематической схемы µL =0,005 м/мм составляет 11 мм, и смещаем силу на 11 мм параллельно самой себе так, чтобы обеспечить относительно точки S3 момент такого же направления, что и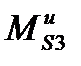 
. Точка пересечения линии действия силы 
и звена 3 дает точку k3.
Для звена 2 заменяем силу инерции 
и момент сил инерции 
одной силой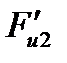 
, равной по величине и направлению силе , но приложенной в центре качания k2 звена. Для его нахождения вычисляем плечо
что в масштабе кинематической схемы µL =0,005 м/мм составляет 4,2 мм, и смещаем силу на 4,2 мм параллельно самой себе так, чтобы обеспечить относительно точки S2 момент такого же направления, что и 
. Точка пересечения линии действия силы 
и звена 2 дает точку k2.
5.2.2 Определение реакций в кинематических парах группы Ассура 
.
Определение реакций начинаем с последней присоединенной группы Ассура, т.е. группы 
.
Вычерчиваем схему группы (µL =0,005 м/мм) в том положении, в котором она находится в механизме в данном положении.
Прикладываем к звену 5 внешние силы Fпс = 1350 Н, G5 = 235,44 Н и 
=1405,800 Н.
По принципу освобождаемости от связей заменяем действие стойки 0 на звено 5 реакцией R05, перпендикулярной к линии движения ползуна 5 (т.к. силы трения не учитываются). Со стороны отсоединенного камня 4 на звено 5 действует реакция R45, перпендикулярная к линии движения ползуна 4.
Рассмотрим равновесие звена 5.
Выбрав масштаб μF = 10 Н/мм, строим план сил для звена 5, последовательно откладывая векторы сил и замыкая силовой многоугольник от точки пересечения направлений неизвестных реакций 
и 
.
По построенному силовому многоугольнику определяем величины реакций, умножая длину соответствующего вектора на масштабный коэффициент плана сил:
Н
Н
Далее рассмотрим равновесие звена 4.
Выбрав масштаб μF = 10 Н/мм, строим план сил для группы 
, последовательно откладывая векторы сил и замыкая силовой многоугольник.
По построенному силовому многоугольнику определяем величины реакций, умножая длину соответствующего вектора на масштабный коэффициент плана сил
Н
5.2.3 Определение реакций в кинематических парах группы Ассура 
Прикладываем к звену 3:
Н, 
Н, 
Н. Вектор 
прикладываем в точке D', развернув вектор R34 на 180˚.
К звену 2 прикладываем: 
Н.
В раскрытых кинематических парах прикладываем реакции. Реакцию R03 представляем в виде нормальной и касательной составляющих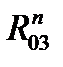 
и 
(
направим вдоль СB, а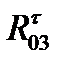 
- перпендикулярно СB). Реакцию R12 представляем в виде нормальной и касательной составляющих 
и 
(
направим вдоль АВ, а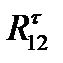 
- перпендикулярно АВ)
Величину 
определим из уравнения моментов всех сил, действующих на звено 3, относительно точки В (центрального шарнира группы):
Откуда
.
Поскольку знак 
из уравнения получен положительным, значит предварительное направление этой составляющей реакции на листе совпадает с предварительно выбранным направлением.
Величину 
определим из уравнения моментов всех сил, действующих на звено 2, относительно точки В (центрального шарнира группы):
Поскольку знак 
из уравнения получен положительным, значит направление этой составляющей реакции на листе соответствует предварительно выбранному направлению.
Поскольку направления реакций 
и 
известны, то, применяя принцип Даламбера, записываем условие равновесия группы Ассура:
.
Выбрав масштаб μF = 10 Н/мм, строим план сил для группы 
, последовательно откладывая векторы сил и замыкая силовой многоугольник от точки пересечения направлений неизвестных реакций 
и 
.
С учетом масштаба величины реакций
Н;
Н;
Н;
Н;
Применяя принцип Даламбера, записываем условие равновесия звена 3:
.
На построенном плане сил по данному векторному уравнению достраиваем недостающий вектор 
, соединяя конец вектора 
с началом вектора 
. Определяем величину этой реакции
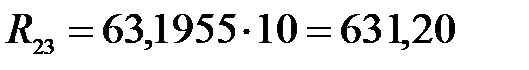Н
