Исследуемый зубчатый механизм, изображенный на рисунке 3 является планетарным. Исходные данные для исследования зубчатого механизма приведены в таблице 3.1
Таблица 3.1 – Исходные данные для исследования зубчатого механизма
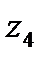
| 
|  , мм , мм
| 
|  , рад/с , рад/с
|

Рисунок 3 – Исходный зубчатый механизм
1) Применим метод коэффициентов (сомножителей). Определение чисел зубьев будем вести используя формулу Виллиса, выразив при этом передаточное отношение планетарного механизма через числа зубьев колес:
 (3.1)
(3.1)
и условие соосности:
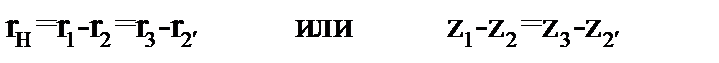 (3.2)
(3.2)
В результате получим формулы для определения чисел зубъев колес:
 , (3.3)
, (3.3)
 , (3.4)
, (3.4)
 , (3.5)
, (3.5)
 . (3.6)
. (3.6)
Вычислим коэффициенты  :
:
 (3.7)
(3.7)
где  при
при  ,
,
 ;
;
 , (3.8)
, (3.8)
 ;
;
 ;
;
 , (3.9)
, (3.9)
 .
.
2) По формуле (3.3) вычислим  , приняв
, приняв 

 условие выполняется, значит, коэффициент q выбран верно и
условие выполняется, значит, коэффициент q выбран верно и 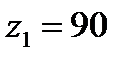 .
.
Аналогично
 ,
,
 ,
,
 .
.
При этом условия правильного зацепления также выполняются:
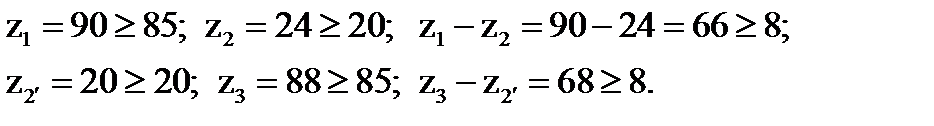
3) Определим фактическое передаточное число редуктора по формуле (3.1):

Найдем относительную погрешность вычислений передаточного отношения:

Значение  не превышает 3 %.
не превышает 3 %.
4) Используя условие «соседства» определим максимально возможное число сателлитов. Вычисления проводим по формуле:
 (3.10)
(3.10)
Изменяя значение  , найдем максимальное значение
, найдем максимальное значение 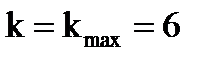 , при котором выполняется неравенство (3.7). Это значение применяем как предварительный результат.
, при котором выполняется неравенство (3.7). Это значение применяем как предварительный результат.
5) Используя условие сборки, уточним число сателлитов. По формуле
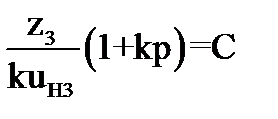 , (3.11)
, (3.11)
вычислим C, изменяя последовательно значения p и k. При этом значение p увеличиваем от 0 до 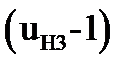 , а значение k уменьшаем от
, а значение k уменьшаем от  до 2. Вычисления ведем до тех пор, пока не получим C – целое число.
до 2. Вычисления ведем до тех пор, пока не получим C – целое число.
Таким образом, получаем 
6) Принимаем окончательное значение  , отвечающее условиям «соседства» и сборки.
, отвечающее условиям «соседства» и сборки.
7) Определим угловую скорость вращения колеса 4:
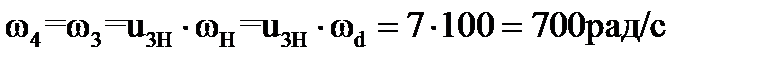 .
.
8) Определим угловую скорость вращения выходного звена (шестерни 5):

Кинематический анализ рычажного механизма
Исходные данные для кинематического анализа рычажного механизма приведены на рисунке 4 и в таблице 4.1.

Рисунок 4 – Исходный рычажный механизм
Таблица 4.1 – Исходные данные для кинематического анализа рычажного механизма
 , м , м
| 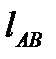 , м , м
|  , м , м
| 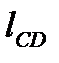 , м , м
|  , м , м
|  , м , м
|  , м , м
|  , м , м
|
| 0,10 | 0,60 | 0,60 | 0,20 | 0,10 | 0,70 | 0,20 | 0,6 |
Построение планов положений механизма
Масштаб планов механизма 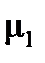 выбираем по длине кривошипа так, чтобы планы механизма занимали примерно от одной трети до половины листа:
выбираем по длине кривошипа так, чтобы планы механизма занимали примерно от одной трети до половины листа:
 , (4.1)
, (4.1)
 м/мм.
м/мм.
Исходя из найденного масштаба планов механизма, найдем длины звеньев и координаты точек вращения:
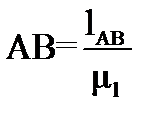 ,
,
 мм;
мм;
 ,
,
 мм;
мм;
 ,
,
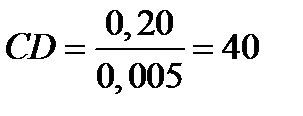 мм;
мм;
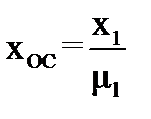 ,
,
 мм;
мм;
 ,
,
 мм;
мм;
 ,
,
 мм.
мм.
Отмечаем точку O. Чертим окружность радиусом  мм. В положении начала рабочего хода, которое соответствует углу 282°47’ проводим линию
мм. В положении начала рабочего хода, которое соответствует углу 282°47’ проводим линию  кривошипа 1 до пересечения с окружностью с центром в точке O.
кривошипа 1 до пересечения с окружностью с центром в точке O.
Из центра C слева от опоры проводим дугу окружности радиусом 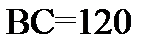 мм.
мм.
Из точки A0 проводим отрезок A0B0=120 мм до пересечения с дугой, радиусом 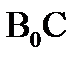 .
.
Из точки C0 на продолжении отрезка  проводим отрезок
проводим отрезок  =40 мм.
=40 мм.
Проводим вертикальную линию на расстоянии  мм от точки C.
мм от точки C.
Из точки 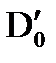 проводим горизонтальную прямую до пересечения с вертикальной линией. Точка пересечения даст точку
проводим горизонтальную прямую до пересечения с вертикальной линией. Точка пересечения даст точку  .
.
Построение планов скоростей и ускорений
Планом скоростей (ускорений) называется рисунок, на котором в масштабе изображены, векторы, равные по модулю и направлению скоростям (ускорениям) различных точек звеньев механизма в данный момент времени. План скоростей (ускорений), построенный для исследуемого положения механизма, является совокупностью нескольких планов скоростей (ускорений) отдельных точек звеньев, у которых полюса планов являются общей точкой – полюсом плана скоростей (ускорений) механизма.






