Визначення залишкової довговічності елемента конструкції

Визначення кількості циклів до руйнування (залишкову довговічність) і аналіз стану елемента при варіації початкової довжини тріщини розглянемо для конструктивного елемента за наявності концентратора напружень і тріщини (рис. 18.5), на який діє асиметричний цикл навантаження.

Дані для розрахунку: матеріал Д16; механічні характеристики матеріалу - критичний коефіцієнт інтенсивності напружень МПа·м , умовна границя текучості = 400 МПа, найбільший коефіцієнт інтенсивності напружень циклу при швидкості поширення тріщини 10 м/цикл, МПа·м , параметр n = 4; коефіцієнт асиметрії циклу r = 0,33; максимальна інтенсивність навантаження 140 МПа; ширина елемента

2 W = 20 см; висота елемента 2 h = 40 см; товщина елемента t = 2 мм; радіус отвору R = 1см.

Рис. 18.5

Величину (

) визначаємо за формулою

де різниця ( - ) являє собою залишкову довговічність елемента конструкції з тріщиною;

, .

Критичну довжину тріщини розраховуємо з умови руйнування Ірвіна, коли (рис. 18.3). У цьому випадку , , 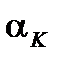= 0,63.

Використовуючи формулу Сімпсона, обчислюємо інтеграл, що входить у вираз (18.5).

Вводимо позначення:

Тоді

(18.6)

де m = 8, m + 1 – кількість вузлових точок, у яких відомі значення підінтегральної функції ƒ().

Для обчислення поправкової функції F ₁(), яка залежить від геометрії елемента і тріщини, використовується графік (рис. 18.2) і табл. 18.1. Розрахунок роблять у табличній формі. Так, для початкової довжини тріщини отримано результати, наведені в табл. 18.3. Підставляючи значення ƒ() у вираз (18.6), обчислюємо величину інтеграла

Після розрахунку значення інтеграла, за формулою (18.5) визначаємо число циклів, яке витримає такий конструктивний елемент до руйнування

Таблиця 18.3.

і	а_і, см		F ₁(a)
	1,300	0,130	1,091	41,8
	1,925	0,193	1,075	20,2
	2,550	0,255	1,074	11,6
	3,175	0,318	1,091	7,0
	3,800	0,380	1,119	4,4
	4,425	0,443	1,158	2,8
	5,050	0,505	1,203	1,9
	5,675	0,568	1,284	1,1
	6,300	0,630	1,374	0,7

Примітка. Аналогічні обчислення можна зробити і при інших значеннях початкової довжини тріщини .

Методичні рекомендації

Аналіз міцності і довговічності деталі, в якій є тріщина можна виконати за допомогою методів механіки руйнування. Під час вивчення механіки руйнування особливу увагу потрібно звернути на поняття коефіцієнта інтенсивності напружень. Необхідно розібратися, від яких факторів залежить коефіцієнт інтенсивності напружень. На основі поняття коефіцієнта інтенсивності напружень формулюється умова руйнувань Ірвіна, будується діаграма циклічної тріщиностійкості і вирішується питання про довговічність елемента конструкції з тріщиною.

Запитання для самоперевірки

Сформулюйте умову крихкого руйнування.

Чим відрізняється квазікрихке руйнування від крихкого?

Назвіть види деформації біля кінчика тріщини.

4. Для чого потрібно знати поле напружень і переміщень біля кінчика тріщини?

5. Що таке коефіцієнт інтенсивності напружень і від яких факторів він залежить?

У чому полягає принцип Бюкнера?

7. Як визначається коефіцієнт інтенсивності напружень для простих конструктивних елементів?

Сформулюйте умову руйнування Ірвіна.

9. Що таке критичний коефіцієнт інтенсивності напружень і як він визначається?

Як розраховується вплив практичної зони?

11. Дайте визначення критичної довжини тріщини. Як побудувати графік який дає змогу знаходити ці величини?

12. Які конструктивні методи використовують для підвищення тріщиностійкості елементів конструкцій?

Який вигляд має діаграма руйнування матеріалу від утоми?

Скільки ділянок має ця діаграма?

15. Які рівняння використовуються для аналітичної характеристики діаграми циклічної матеріалостійкості матеріалу?

Як визначити залишкову довговічність деталі з тріщиною?

17. У чому полягає основна ідея методу визначення граничного стану, в якій є елементи конструкцій, у яких є концентратори напружень?

СПИСОК ЛІТЕРАТУРИ

1. Астанін В. В. Технічна механіка. Частина II. Опір матеріалів: навч. посіб. / В. В. Астанін. — К.: Вид-во Нац. авіа. ун-ту «НАУ-друк», 2009. — 192 с.

2. Астанін В. В. Динаміка та міцність машин у прикладах і задачах: навч. посіб. / В. В. Астанін, М. М. Бородачов, М.І. Савченко. — К.: НАУ, 2008. — 184 с.

3. Бородачов М. М. Опір матеріалів: навч. посіб. / М. М. Бородачов, М. І. Савченко. — К.: НАУ, 2003. — 424 с.

4. Бородачев Н.М. Расчет балок на упругом основании: метод. указ. / Н. М. Бородачев — К.: КИИГА, 1979. — 56 с.

5. Беляев Н. М. Сопротивление материалов. — 15-е изд. / Н. М. Беляев М.: Вид-во Наука, 1976. — 607 с.

6. Бойл Дж. Анализ напряжений в конструкциях при ползучести. Пер. с англ. / Дж. Бойл, Дж. Спенс — М.: Мир, 1986. — 360 с.

7. Дарков А. В. Сопротивление материалов. / А. В. Дарков, Г. С. Шпиро — М.: Высш. шк., 1989. — 622 с.

8. Коллинз Дж. Повреждение материалов в конструкциях / Пер. с англ. / Коллинз Дж. — М.: Мир, 1984. — 624с.

9. Малинин Н. Н. Прикладная теория пластичности и ползучести. Н. Н. Малинин. — М.: Машиностроение, 1968. — 400 с.

10. Писаренко Г. С. Опір матеріалів: підруч. / Г. С. Писаренко, Е. С. Квітка, Е. С. Уманський — К.: Вища шк., 1993. — 655 с.

11. Писаренко Г. С. Справочник по сопротивлению материалов. -е изд., перераб. и доп. / Г. С. Писаренко, А. П. Яковлєв, В. В. Матвеев — К.: Наук. думка, 1988. — 736 с.

12. Справочник машиностроителя: в 6 т. / Под ред. акад. АН УССР С. В. Серенсена. — М.: Машгиз, 1968. — Т.3. — 651 с.

13. С правочник по коэффициентам интенсивности напряжений. В 2-х томах. / Под ред. Ю. Мураками. — М.: Мир, 1990. т.1 —

448 с., т. 2 – 565 с.

14. Сопротивление материалов / Под общей ред. А. Ф. Смирнова. 3-е изд., перераб. и доп. — М.: Высш.шк., 1975. — 480 с.

15. Хеллан К. Введение в механику разрушения. / К. Хеллан — М.: Мир, 1988. — 364 с.

16. Химушин Ф. Ф. Жаропрочные стали и сплавы. / Ф. Ф. Химушин — Изд-во «Металлургия», 1969, 2-е изд., — 752 с.

17. ГОСТ 8509-93. Уголки стальные горячекатаные равнополочные. Сортамент. — Введ.01.01.97.

18. ГОСТ 8510-86. Сталь прокатная угловая неравнополочная. Сортамент. — Введ. 01.07.87.

19. ГОСТ 8239-89. Двутавры стальные горячекатанные. Сорта-мент. — Введ. 01.07.90.

20. ГОСТ 8240-97. Швеллеры стальные горячекатаные. Сортамент. — Введ. 01.01.2002.