Приклад 1. Ступінчастий стержень жорстко закріплений в абсолютно непіддатливі стінки і навантажений однією поздовжньою силою (рис. 16.2).
Рис. 16.2
Потрібно:
1) визначити допустиме навантаження 
і граничнодопустиме навантаження 
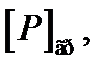якщо діаграма деформування відповідає ідеальному пружно-пластичному тілу (рис.16.3), а коефіцієнт запасу k = 1,5. Пластичність без зміцнення називається ідеальною.
Рис. 16.3
2) зробити висновок про те, який метод розрахунку найповніше використовує несучу здатність стержня.
Дані для розрахунку:
F =7,2 см2; матеріал - сталь Ст-45; 
=360 МПа.
Розв'язання:
1. Розкриваємо статичну невизначеність системи.
Задана система один раз статично невизначувана. Припустимо спочатку, значення сили Р таке, що у всіх поперечних перерізах стержня
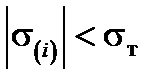, і = 1, 2, …
Для розв’язання задачі необхідно скласти такі рівняння:
Рівняння статики:
(16.2)
Рівняння сумісності деформацій
(16.3)
Визначаємо нормальні сили на ділянках стержня. Проводимо переріз 1-1; 2-2. Отримуємо
(16.4)
Використовуючи закон Гука і співвідношення (16.4), рівняння (16.2) і (16.3) подамо у вигляді:
(16.5)
(16.6)
Після перетворень рівняння (16.6) набуває вигляду:
(16.7)
Розв'язуючи сумісно рівняння(16.5) і (16.7), знаходимо:
Розраховуємо напруження на ділянках стержня:
, 
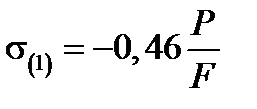2. Знаходимо величину небезпечного навантаження.
Оскільки 
, то при збільшенні зовнішньої сили P, напруження на першій ділянці, раніше досягне значення границі текучості. Це відбудеться, якщо
Звідси 
Якщо на будь-якій ділянці стержня напруження досягають границі текучості, то рівняння сумісності деформацій (16.7) втрачає зміст, оскільки дія закону Гука обмежена границею пропорційності 
.
Так як 
, то рівняння рівноваги (16.5) при 
буде мати вигляд:
.
Знаходимо значення нормальних сил на ділянках стержня:
стержень буде зберігати свою несучу здатність, оскільки на другій ділянці напруження буде менше величини границі текучості і дорівнюватиме:
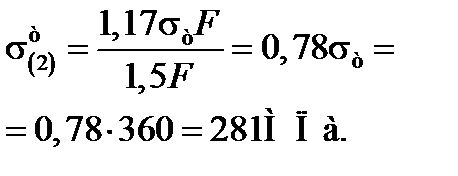
За отриманими даними будуємо епюри нормальних сил і напружень при 
(рис. 16.4)
3. Розраховуємо величину граничного навантаження 
.
За подальшого збільшення навантаження напруження на першій ділянці буде постійним 
, а на другій - збільшуватиметься поки не досягне границі текучості 
, що призведе до втрати несучої здатності стержня. Такий стан називають граничним, а відповідну йому силу визначають за умовою рівноваги, яка матиме вигляд:
Звідси 
При 
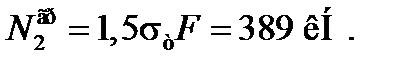
За отриманими даними будуємо епюри нормальних сил і напружень при 
(рис.16.5).
Знаходимо значення допустимого і граничнодопустимого навантажень:
Таким чином, значення граничнодопустимого навантаження більше значення допустимого навантаження на
Приклад 2. Для заданої балки треба визначити розміри поперечного перерізу за допустимими напруженнями та руйнівним навантаженням.
Для поперечного перерізу, розрахованого за допустимими напруженнями, потрібно знайти величини небезпечного згинального моменту 
і граничного згинального моменту 
.
Діаграма деформування матеріалу балки відповідає ідеальному пружно-пластичному тілу (рис. 16.3).
Беремо: 
; 
; k = 1,5.
Дані для розрахунку: q =10 кН/м; а = 1 м; n = 2. Матеріал сталь - Ст-45, 
МПа. Схема балки зображена на рис. 16.6, поперечний переріз – на рис. 16.7.
Рис. 16.6
1. Будуємо епюри згинальних моментів M.
Визначаємо опорні реакції:
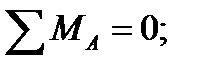
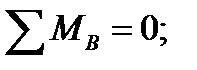
Перевірка:
Розбиваємо балку на ділянки. Для кожної ділянки складаємо рівняння згинальних моментів.
Маємо:
I ділянка: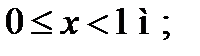 
при x = 0 М = 0;
при x = 1м М = 26 кНм.
II ділянка: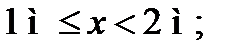 
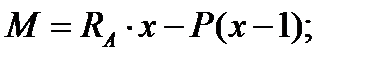
при x = 1 м М = 26 кНм;
при x = 2 м М = 42 кНм.
III ділянка: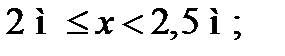 
при x = 2 м М = 42 кНм;
при x = 3 м М = 48,8 кНм.
IV ділянка: 
при x = 3 м М = 48,8 кНм;
при x = 4 м М = 24 кНм.
V ділянка: 
при x = 4 м М = 24 кНм;
при x = 5 м М =0.
На основі отриманих результатів будуємо епюру згинальних моментів (рис. 16.6).
2. Підбираємо поперечний переріз балки.
Визначаємо величину допустимого напруження:
Максимальне значення згинального моменту:
Осьовий момент опору за умовою міцності при плоскому згинанні дорівнює:
Визначаємо величину осьового моменту опору для заданого поперечного перерізу (рис. 16.7):
Звідки розміри поперечного перерізу балки за допустимими напруженнями дорівнюють:
Виконуємо підбір поперечного перерізу балки методом руйнівних навантажень. Осьовий пластичний момент опору визначається за умовою:
Водночас 
дорівнює сумі статичних моментів верхньої і нижньої частин перерізу відносно нейтральної осі:
Розміри поперечного перерізу за руйнівними навантаженнями дорівнюютьзу за ідносно нейтральної осіу балки:
2. Для поперечного перерізу балки, знайденого по допустимим напруженням знаходимо величину небезпечного згинального моменту:
Визначаємо величину граничного згинального моменту:
Відношення граничного згинального моменту до небезпечного рівня:
Методичні рекомендації
Під час вивчення цього розділу передусім слід запам’ятати, що таке допустимі й небезпечні навантаження, а також граничне і граничнодопустиме навантаження. Далі необхідно розглянути дійсну діаграму деформування матеріалу і її можливі схематизації, ознайомитися з методами розрахунку на розтягання і стискання бруса з ідеального пружно-пластичного матеріалу, а також з матеріалу з лінійним зміцненням, розглянути кручення бруса з ідеального пружно-пластичного матеріалу. Потрібно навчитися розв’язувати задачі на згинання балки з ідеального пружно-пластичного матеріалу, розібратися, що являє собою пластичний шарнір і яка величина називається осьовим пластичним моментом опору перерізу, що таке залишкове напруження і які існують методи їхнього визначення (на прикладі балки).
Запитання для самоперевірки
1. Що таке небезпечне і допустиме навантаження?
2. Що являють собою граничне і граничнодопустиме навантаження?
3. Чому при небезпечному навантаженні в багатьох випадках не відбувається повного вичерпання несучої здатності конструкції?
4. Чому розрахунок конструкції за граничними (руйнівними) навантаженнями є більш економічним, ніж розрахунок за допустимим напруженням?
5. Чим відрізняється дійсна діаграма деформування від звичайної (умовної)?
6. Як проводиться схематизація діаграми деформування?
7. Який вигляд мають діаграми деформування у випадку ідеальної пластичності та у випадку лінійного зміцнення?
8. В якій послідовності проводиться розрахунок на розтягання і стискання бруса з ідеального пружно-пластичного матеріалу? Як можна розрахувати лінійне зміцнення?
9. Напишіть основні формули, пов’язані з крученням бруса з ідеального пружно-пластичного матеріалу.
10. Що таке пластичний шарнір?
11. Яка величина називається осьовим пластичним моментом опору перерізу?
12. Як виконують розрахунок балки з ідеального пружно-пластичного матеріалу? Як визначити граничне навантаження для балки?
13. Які напруження називаються залишковими?
14. Як визначають залишкові напруження?
