Для зображеного на рис. 18.1 конструктивного елемента розрахувати залишкову міцність за наявності в ньому концентратора напружень і тріщини, зробити висновок про міцність конструктивного елемента, виконаного з матеріалу Д16.
Рис. 18.1
Дані для розрахунку:
характеристики матеріалу Д16: критичний коефіцієнт інтенсивності напружень КС = 84,4 МПа·м1/2 умовна границя текучості  МПа; інтенсивність навантаження
МПа; інтенсивність навантаження  МПа, ширина елемента 2 W = 20 см; висота елемента 2 h = 40 см, товщина елемента t = 2 мм; радіус отвору R = 1 см.
МПа, ширина елемента 2 W = 20 см; висота елемента 2 h = 40 см, товщина елемента t = 2 мм; радіус отвору R = 1 см.
Для пластини з центральним круговим отвором залежність коефіцієнта інтенсивності напружень нормального відриву 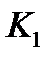 від довільної інтенсивності навантаження
від довільної інтенсивності навантаження  , прикладеного до елемента, записується у вигляді
, прикладеного до елемента, записується у вигляді
К 1 = F 1(a)  a =
a =  , (18.1)
, (18.1)
де  - поправкова функція, що залежить від геометрії елемента і тріщини.
- поправкова функція, що залежить від геометрії елемента і тріщини.
Для обчислення функції  користуються графіком (рис. 18.2) і табл. 18.1 [13].
користуються графіком (рис. 18.2) і табл. 18.1 [13].
Рис. 18.2.
Таблиця 18.1.
| а/W | с/R | F 1(a) | а/W | с/R | F 1(a) | |
| 0,12 | 0,2 | 0,994 | 0,24 | 1,4 | 1,072 | |
| 0,13 | 0,3 | 1,091 | 0,26 | 1,6 | 1,074 | |
| 0,14 | 0,4 | 1,072 | 0,30 | 2,0 | 1,083 | |
| 0,15 | 0,5 | 1,078 | 0,40 | 3,0 | 1,128 | |
| 0,16 | 0,6 | 1,079 | 0,50 | 4,0 | 1,203 | |
| 0,18 | 0,8 | 1,077 | 0,60 | 5,0 | 1,319 | |
| 0,20 | 1,0 | 1,073 | 0,70 | 6,0 | 1,502 | |
| 0,22 | 1,2 | 1,072 | 0,80 | 7,0 | 1,82 |
Обчислення коефіцієнта інтенсивності напружень 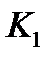 нормального відриву роблять у вигляді таблиці 18.2.
нормального відриву роблять у вигляді таблиці 18.2.
Таблиця 18.2
| a | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| F 1(a) | 1,073 | 1,083 | 1,128 | 1,203 | 1,319 | 1,502 | 1,820 |
| а, 10-2 м | |||||||
 , м1/2 , м1/2
| 0,251 | 0,307 | 0,354 | 0,396 | 0,434 | 0,469 | 0,501 |
| К 1, МПа.м1/2 | 37,70 | 46,54 | 55,90 | 66,69 | 80,14 | 98,62 | 127,6 |
| ry, 10-2 м | 0,141 | 0,216 | 0,311 | 0,442 | 0,639 | 0,967 | 1,621 |
| a + ry, 10-2 м | 2,141 | 3,216 | 4,311 | 5,442 | 6,639 | 7,967 | 9,621 |
| sк , МПа | 313,7 | 254,2 | 211,5 | 177,3 | 147,5 | 119,8 | 92,5 |
| a + ry*, 10-2 м | 2,709 | 3,709 | 4,709 | 5,709 | 6,709 | 7,709 | 8,709 |
| a * | 0,271 | 0,371 | 0,471 | 0,571 | 0,671 | 0,771 | 0,871 |
| F 1(a *) | 1,090 | 1,103 | 1,181 | 1,285 | 1,449 | 1,727 | - |
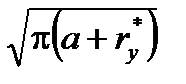 , м1/2 , м1/2
| 0,292 | 0,341 | 0,385 | 0,424 | 0,459 | 0,492 | - |
| sк *, МПа | 267,6 | 224,3 | 185,6 | 154,9 | 126,8 | 99,3 | - |
За отриманими даними будуємо графік залежності К  від довжини тріщини а (рис. 18.3).
від довжини тріщини а (рис. 18.3).
Рис. 18.3
Для аналізу напруженого стану біля вершини тріщини, де концентрація напружень зумовлена малим радіусом заокруглення вершини тріщини, використовують формули для визначення напружень  У випадку нормального відриву при плоскому напруженому стані ці формули мають вигляд:
У випадку нормального відриву при плоскому напруженому стані ці формули мають вигляд:
 ;
;
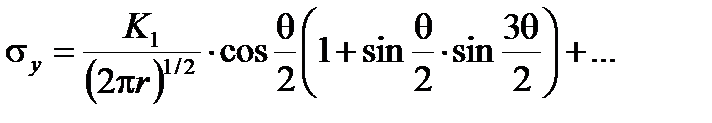 ;
;
 .
.
Використовуючи ці формули й умову пластичності Мізеса, визначаємо розмір пластичної зони біля вершини тріщини
 ,
,
де  - умовна границя текучості матеріалу.
- умовна границя текучості матеріалу.
У момент руйнування К 1 = КС. Тоді граничний розмір пластичної зони при  = 0 можна визначити за формулою:
= 0 можна визначити за формулою:
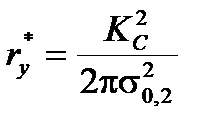 . (18.2)
. (18.2)
У цьому випадку при КС = 84,4 МПа·м 
 м = 0,709 см.
м = 0,709 см.
Умові плоского напруженого стану відповідає умова 
Для заданого елемента  - умова виконується.
- умова виконується.
Отже, у цьому випадку маємо злам у вигляді зрізу. Таким чином, пластична зона поширюється на всю товщину зразка, а елементи крихкого зламу відсутні. При цьому досягається невелика міцність матеріалу. Критичне напруження визначаємо з урахуванням і без урахування пластичної зони.
З умови Ірвіна критерій розвитку тріщини нормального відриву має вигляд К  = КС. Отже, у момент початку нестійкого поширення тріщини з урахуванням формули (18.1)
= КС. Отже, у момент початку нестійкого поширення тріщини з урахуванням формули (18.1)
 .
.
Тоді критичне напруження без урахування пластичної зони можна визначити за формулою:
 . (18.3)
. (18.3)
Результати обчислення 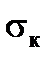 за формулою (18.3) подано в табл. 18.2 і на рис. 18.4.
за формулою (18.3) подано в табл. 18.2 і на рис. 18.4.
Критичне напруження з урахуванням пластичної зони розраховуємо за формулою
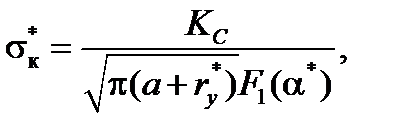
 (18.4)
(18.4)
де  визначається за формулою (18.2).
визначається за формулою (18.2).
У табл. 18.2 і на рис. 18.4 подано значення величини  , обчислені за формулою (18.4). Поправкову функцію
, обчислені за формулою (18.4). Поправкову функцію 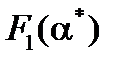 знаходимо за графіком (рис. 18.2) чи за табл. 18.1.
знаходимо за графіком (рис. 18.2) чи за табл. 18.1.
За результатами розрахунків можна зробити висновок про міцність цього конструктивного елемента. Тріщина в елементі поширюватися не буде, якщо виконується умова Ірвіна:
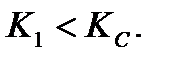
У цьому випадку критерій Ірвіна виконується за умови, що довжина тріщини в елементі буде не більше критичної довжини  см.
см.
Рис. 18.4.
На рис. 18.4: 1 - без урахування пластичної зони поблизу вершини; 2 - з її урахуванням.






