Рассмотрим следующую задачу. Из 67 студентов 47 знают английский язык, 35 -немецкий язык и 23 оба языка. Сколько студентов знают хотя бы один язык, сколько студентов не знают ни одного языка?
Разобьем множество всех студентов на подмножества, не имеющие общих элементов. Первое подмножество составят те, кто знает хотя бы один язык, второе - те, кто не знает ни одного языка. В свою очередь первое подмножество можно разбить на три непересекающихся подмножества: те, кто знает только английский; те, кто знает только немецкий; те, кто знают оба языка. Нам дано, что последнее подмножество состоит из 23 человек. Но так как английский знает 47 студентов, то только английским владеют 47 - 23 = 24 студента. Точно так же, только немецким владеют 35 - 23 =12 студентов. Отсюда следует, что число студентов, владеющих хотя бы одним языком, равно 23 + 24 + 12 = 59. А так как всего студентов 67, то на долю, не владеющих ни одним языком, приходится 67 – 59 = 8 студентов.
Полученные результаты запишем следующим образом. Число студентов, владеющих языками, равно сумме числа студентов, владеющих английским (а может быть и немецким), и числа студентов, владеющих немецким (а может быть и английским), минус число студентов, владеющих обоими языками 47 + 35 - 23 = 82 - 23 = 59 Число студентов, не знающих языков, равно общему числу студентов минус число студентов, владеющих хотя бы одним языком 67 - 59 = 8 Число студентов, владеющих только английским, равно числу студентов, владеющих английским (а может быть и немецким) минус число студентов, владеющих обоими языками.
После решения этой частной задачи перейдем к решению следующей общей задачи. Пусть имеется множество А, состоящее из двух подмножеств А1 и А2, так что А=А1UА2.Число элементов множества А1 известно и равно |А1|, число элементов множества А2 также известно - |А2|. Спрашивается, каково число элементов в множестве А. Очевидно, сумма |А1| + |А2| есть число, которое мы получим перечислив все элементы множества А1, а затем - все элементы множества А2, но при этом общие элементы обоих множеств А1 и А2 будут перечислены дважды. Общие элементы множеств А1 и А2 есть, по определению, пересечение (произведение) этих множеств - А1∩А2, число же элементов в этом пересечении есть |А1∩А2|. Итак, имеем очевидное соотношение
|А1| + |А2| = |А1UА2| + |А1∩А2|, отсюда получаем решение задачи
|А| = |А1UА2| = |А1| + |А2| - |А1∩А2|.
Получим теперь решение аналогичной задачи в случае, когда множество А состоит из трех подмножеств А = А1UА2UА3.
|А|=|А1UА2UА3|=|А1|+|А2|+|А3|-|А1∩А2|-|А3∩А2|-|А1∩А3|+|А1∩А2∩А|.
Пример. На курсе обучаются - либо девушки, либо блондины, либо любители математики. На курсе 20 девушек, из них 12 блондинок, и одна блондинка любит математику. Всего на курсе 24 студента-блондина, математику из них любят 12, а всего студентов (юношей и девушек), которые любят математику, - 17, из них 6 девушек. Сколько студентов на курсе?
А1 - множество девушек,
А2 - множество блондинов,
А3 - множество студентов, любящих математику.
А1UА2UА3 – все студенты обучающиеся на курсе.
Требуется найти |А1UА2UА3|. Для этого надо определить множества и число элементов в них, таких, как
А1∩А2 - множество блондинок,
А1∩А3 - множество студенток, любящих математику,
А3∩А2 - множество блондинов (юношей и девушек), любящих математику,
А1∩А2∩А3 - множество блондинок, любящих математику. Тогда:
|А1UА2UА3|=|А1|+|А2|+|А3|-|А1∩А2|-|А3∩А2|-А1∩А3|+|А1∩А2∩А3|=
= 2 + 24 + 17 – 12 – 6 – 12 + 1 = 32.
Установим теперь общую формулу для нахождения числа элементов объединения нескольких множеств. Пусть имеется
А = А1UА2UА3U…….UАn.
Тогда справедливо следующее соотношение:
|А| = |А1| + |А2| + |А3| +…+ |Аn| - |А1∩А2| - |А3∩А2| - |А1∩А3| -…- |Аn-1∩Аn|+|А1∩А2∩А3| + |А1∩А2∩А4| +…..+ |Аn-2∩Аn-1∩Аn|+….+ +(-1)n|А1∩А2∩А3∩…∩Аn|.
Данная формула интуитивно правдоподобна, ее точное доказательство проводится довольно просто, аналогично тому, как это было сделано при n =3.
Рассматриваемая формула носит название формулы включений-исключений. Это название естественно вытекает из конструкции формулы - сначала включаются в расчет все элементы, обладающие хотя бы одним из свойств 1,2,... n, потом исключаются из расчета элементы, обладающие, по крайней мере, двумя из этих свойств, включаются имеющие, по крайней мере, три свойства и т.д.
Формула включений-исключений представляет один из важнейших комбинаторных методов - принцип включения и исключения, известен также под названиями: символический метод, принцип перекрестной классификации, метод решета.
Рассмотрим некоторые задачи, при решении которых полезно использование формулы включений-исключений.
Пример. Из 100 студентов английский язык знают 28 студентов, немецкий - 30, французский - 42, английский и немецкий - 8, английский и французский - 10, немецкий и французский - 5, все три языка знают 3 студента. Сколько студентов не знают ни одного языка?
Обозначим через А множество студентов, знающих хотя бы один язык, через 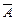 - множество студентов, не знающих ни одного языка, очевидно, А = А1UА2UА3, где А1 -множество студентов, знающих английский, А2 - множество студентов знающих немецкий, А3 - множество студентов, знающих французский язык, I - множество всех студентов. Ответ на поставленный вопрос дается теперь непосредственным применением формулы включений-исключений
- множество студентов, не знающих ни одного языка, очевидно, А = А1UА2UА3, где А1 -множество студентов, знающих английский, А2 - множество студентов знающих немецкий, А3 - множество студентов, знающих французский язык, I - множество всех студентов. Ответ на поставленный вопрос дается теперь непосредственным применением формулы включений-исключений
| 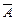 | =| I |-|А1UА2UА3|=| I | -|А1| -|А2| - |А3| + |А1∩А2| + |А3∩А2| + |А1∩А3| - |А1∩А2∩А3| = 100 - 28 - 30 - 42 + 8 + 10 + 5 – 3 = 20.
| =| I |-|А1UА2UА3|=| I | -|А1| -|А2| - |А3| + |А1∩А2| + |А3∩А2| + |А1∩А3| - |А1∩А2∩А3| = 100 - 28 - 30 - 42 + 8 + 10 + 5 – 3 = 20.
При решении задач, аналогичных рассмотренной, кроме формулы включений-исключений, полезно применять и законы Моргана.
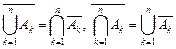 .
.
Рассмотрим задачу математика Доджсона, который под псевдонимом Льюиса Керрола известен как автор "Алисы в стране чудес".
"В бою 70 из 100 пиратов потеряли один глаз, 75 - одно ухо, 80 - одну руку, 85 -одну ногу. Каково минимальное число пиратов, потерявших одновременно глаз, ухо, руку и ногу?"
Обозначим через A1 множество одноглазых, через А2 - множество одноухих, через A3 - множество одноруких, через A4 - множество одноногих.
Ясно, что в задаче требуется оценить 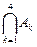 Очевидно, что все множество пиратов (универсальное множество) состоит из двух непересекающихся множеств: подмножества
Очевидно, что все множество пиратов (универсальное множество) состоит из двух непересекающихся множеств: подмножества 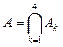 и его дополнения
и его дополнения 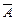 .
.
I = AU 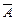 = AU
= AU  = AU
= AU  ,
,
следовательно:
| I | = | А1∩А2∩А3∩А4| + |  U
U  U
U  U
U  |
|
откуда:
| А1∩А2∩А3∩А4| = | I | - |  U
U  U
U  U
U  |
|
Используя теперь очевидное неравенство
|  U
U  U
U  U
U  |≤ |
|≤ |  | + |
| + |  |+ |
|+ |  | + |
| + |  |
|
получим неравенство
| А1∩А2∩А3∩А4| ≥ | I | - |  | - |
| - |  | - |
| - |  | - |
| - |  |
|
Подставляем в него данные задачи | I | = 100,
|  | = | I \ A 1,| = | I | - |A1| = 100 - 70 = 30, аналогично:
| = | I \ A 1,| = | I | - |A1| = 100 - 70 = 30, аналогично:
|  | = 25, |
| = 25, |  | = 20, |
| = 20, |  | = 15, получим решение задачи
| = 15, получим решение задачи
| А1∩А2∩А3∩А4| ≥ 100 – 30 – 25 – 20 – 15 = 10






