Схема размещения частиц по ячейкам является как бы образным языком многих важных практических задач. Этот язык, эта схема позволяет рассматривать, исследовать и решать единым образом весьма разные на первый взгляд задачи. Рассмотрим некоторые из таких задач.
Дни рождения. Распределение дней рождения n человек соответствует размещению n различных частиц по k = 365 (положим, что в году 365 дней) ячейкам.
Стрельба по мешениям. При стрельбе по k мишеням пули соответствуют одинаковым частицам, мишени - ячейкам.
Классификация. Классификация n несчастных случаев по дням недели, в которые они происходят, эквивалента размещению n шаров по 7 ячейкам.
Задача о лифте. Лифт отправляется с n пассажирами и останавливается на k этажах. Распределение пассажиров по группам соответственно этажу, на котором они выйдут, соответствуют размещению n различных частиц по k ячейкам.
Игральные кости. Различные исходы бросания n игральных костей соответствуют размещению n различных частиц по k = 6 ячейкам.
Игральные карты. Распределение карт при игре в бридж соответствует размещению n =52 различных частиц по k = 4 ящикам при условии, что в каждом ящике размещается 13 частиц.
Случайные числа. Каждой последовательности n случайных цифр отвечает размещение n различных частиц по k =10 ячейкам.
Статистическая квантовая физика. Эта наука изучает, как распределяются по своим свойствам физические частицы. При этом множество всех возможных состояний называется фазовым пространством. Все фазовое пространство делится на k мелких областей - фазовых состояний. Рассматриваемые n частиц могут находиться в этих фазовых состояниях. Какими свойствами обладают частицы и какими способами они размещаются в фазовом пространстве состояний, определяется статистикой, которой подчиняются частицы.
В классической статистической физике, созданной Максвеллом и Больцманом, частицы считаются различимыми друг от друга. В этом случае возможны kn различных способов нахождения n частиц в k состояниях. Такой статистике подчиняются в первом приближении молекулы газа.
Оказалось, что этой статистике подчиняются не все физические частицы. Фотоны, атомные ядра и атомы, содержащие четное число элементарных частиц, подчиняются иной статистике, разработанной Эйнштейном и индийским ученым Бозе. В статистике Бозе-Эйнштейна частицы считаются неразличимыми, поэтому имеет значение лишь то, сколько частиц попало в ту или иную ячейку, а не то, какие именно частицы туда попали. При таком подходе количество способов размещения будет равно:
.
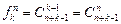Однако для многих частиц, например, таких, как электроны, протоны, нейтроны, не годится и статистика Бозе-Эйнштейна. Для этих частиц в одном фазовом состоянии может находиться не более одной частицы, причем частицы неразличимы между собой. В этом случае общее число распределений частиц по состояниям равно числу размещений n одинаковых частиц в k ячейках, а это число равно числу сочетаний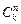 
. Такая статистика называется статистикой Ферми-Дирака.
Комбинаторика и множества
Основные задачи теории конечных множеств состоят в следующем: зная количество элементов некоторых множеств, вычислить количество элементов других множеств, которые составлены из первых с помощью некоторых операций.
