95*. Реактивный самолет имеет четыре двигателя, развивающих силу тяги 20000Н каждый. Сколько керосина израсходуют двигатели на перелет в 5000 км? Теплотворная способность керосина 45.106 Дж/кг, КПД двигателя 25 %.
96*. Автомобиль «Москвич» расходует 5,67 кг бензина на 50 км пути. Определить мощность, развиваемую двигателем, если скорость движения 90 км/ч и КПД двигателя 22 %. Теплотворная способность бензина 45.106 Дж/кг.
97**. Поезд массой М идет по горизонтальному пути со скоростью υ. Тепловоз сжигает при этом за время τ топливо массой m. КПД двигателя равен η. Какую скорость разовьет поезд при тех же условиях на пути с уклоном вверх α? Удельная теплота сгорания топлива q.
| Требования к оформлению отчетов по домашним задачам: ü для учащихся, работающих на уровне А – оформить в отдельной тетради решение всех задач без «звездочек» - 33 задачи; ü для учащихся, работающих на уровне В – перерешать в черновике все задачи без «звездочек» и оформить в отдельной тетради решение всех задач с одной «звездочкой» - 28 задач; ü для учащихся, работающих на уровне С – перерешать в черновике все задачи без «звездочек» и с одной «звездочкой» и оформить в отдельной тетради решение всех задач с двумя «звездочками» - 30 задач. При сдаче отчетов указать, какой процент задач выполнен. |
Критерии оценивания на зачете № 3 «Задачи для самостоятельного решения».
В рамках этого зачета Вы получите две отметки. Для этого Вы сдаете учителю тетради с оформленными решениями задач и отчет о количестве решенных Вами домашних задач. Первую отметку Вы получаете за количество решенных задач.
Критерии отметки за количество решенных задач:
|
| Критерии оценивания на зачете № 4 «Контрольная работа». На этом зачете Вам будут предложены задачи, заранее Вам не раскрытые, но по уровню сложности такие же, как и открытые задачи для самостоятельного решения. Критерии оценивания на этом зачете такие же, как и на зачете № 3. |
V. ОТВЕТЫ, ПОДСКАЗКИ, ПРИМЕРЫ
Ответы и подсказки к тесту
1. Б. 2. Б. 3. Внутренняя энергия газа уменьшится. Уменьшится средняя кинетическая энергия молекул: 
, которая однозначно определяет температуру газа: 
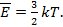Следовательно, уменьшится температура, а значит и внутренняя энергия газа. 4. Б. 5. В. 6**. В. Подсказка: необходимо учитывать количество степеней свободы у двухатомных и трехатомных молекул. 7**. Б. 8**. В. Подсказка: импульс, передаваемый стенке сосуда каждой молекулой при ударе, зависит только от импульса поступательного движения молекулы. 9. В. Подсказка: внутренняя энергия идеального газа определяется только его температурой. 10. Г. Подсказка. Внутренняя энергия одноатомного идеального газа равна: U = 3/2 vRT. Но согласно уравнению Менделеева-Клапейрона: vRT = РV. Следовательно, U =3/2 РV, то есть чем больше произведение РV, тем больше внутренняя энергия газа. 11*. Г. Подсказка: согласно основному уравнению МКТ: р = 
nm 0 
= 
= 
= = 
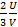, где: 
. 12. Б. 13. А. Подсказка: 
. Следовательно: 
. 14**. В. 15. В. 16*. Б. 17*. В. 18*. Б. 19*. В. 20*. Г. 21. В. 22. Б. 23. В. 24. Б. 25. В. 26*. В. 27**. Б. 28*. А. 29. В. 30. Г. 31. А. 32. Г. 33. А. 34*. Г. Подсказка. Из графика видно, что зависимость p (V) прямо пропорциональная: во сколько раз увеличивается температура, во столько же раз увеличивается давление. Следовательно, этот процесс изохорный: V = const - работа газом не совершается. 35*. Г. 36**. Б. 37*. Д. 38. В. Подсказка. Согласно первому закону термодинамики, количество теплоты, переданное газу, идет на увеличение внутренней энергии газа и на совершение им работы над внешними телами: Q = Δ U + А. Отсюда можно определить значение изменения внутренней энергии газа. 39. Г. Подсказка. Обратите внимание, что сам газ при этом совершил отрицательную работу. 40. В. 41. Г. Подсказка. При адиабатическом процессе Q = 0. 42. Поднимаясь в менее плотные слои атмосферы теплый воздух расширяется и совершает при этом работу, охлаждаясь. 43. Затрачиваемая механическая энергия при накачивании воздуха в шину превращается во внутреннюю энергию сжатого воздуха, и температура его повышается. При этом насос также нагревается. 44. А. Подсказка. Ответ зависит от знака совершенной газом работы и от знака изменения внутренней энергии газа: Q = Δ U + А. Если оба знака положительны, то Q > 0, и наоборот. 45*. Б. 46. А. 47*. В. 48*. А. 49*. А. 50*. Г. 51*. Б. 52*. Б. 53*. В. 54*. Г. 55*. Б. 56**. В. 57**. В. Подсказка. В соответствии с определением молярной теплоемкости, еe значение можно найти следующим образом: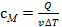 
. Главное, значения Q и v Δ Т выразить через взаимно сокращаемые множители. 58**. А. 59**. А. 60**. В. 61**. Б. 62**. А. 63**. В. 64**. Б. 65**. Г. 66**. В. 67. Нет. КПД тепловых машин меньше 100% в основном за счет того, что одним из условий работы теплового двигателя является необходимость передачи холодильнику части количества теплоты, получаемого от нагревателя. 68. Нагревателем – ракетное топливо, холодильником – окружающая среда. 69. А. Подсказка. Полезная работа двигателя A, количество теплоты Q н, получаемое от нагревателя рабочим телом и количество теплоты, передаваемое им холодильнику Q х, всегда связаны друг с другом так: A = Q н - Q х. 70*. Б. 71*. Г. 72*. А. 73*. Г. 74*. В. 75**. А. 76**. В. 77**. А. 78*. В. 79*. Б. 80*. В. 81**. В. 82**. А. 83**. Б. 84**. Д. 85**. Б. 86**. Б. 87. Г. 88. Б. 89. А. 90. Г. 91. Г. 92. Б. 93. В. 94. Механическая энергия волн превращается во внутреннюю энергию. 95. Когда гвоздь перемещается, кинетическая энергия молотка частично превращается в кинетическую энергию гвоздя и частично во внутреннюю энергию гвоздя и дерева. Но когда гвоздь не перемещается, то передаваемая молотком энергия превращается только во внутреннюю энергию. 96. Нет. Часть кинетической энергии метеоритов при падении на Землю превращается в его внутреннюю энергию из-за работы силы сопротивления воздуха. В результате метеориты накаляются до свечения. У луны же нет атмосферы. 97*. А.
Ответы и подсказки к задачам
1. 20 кДж. 2*. 15 кДж. 3*. 9 кДж. 4**. ≈ 113 К, если пренебречь теплоемкостью сосуда. 5. 22,4 кДж. 6. 897 Дж. 7**. 3,7 кДж, 2,2 кДж, 1,5 кДж. Подсказка. Для двухатомного газа количество степеней свободы молекул i = 5, причем i = 3 приходится на долю поступательного движения и i = 2 – на долю вращательного движения. 8**. 83 кДж. 9*. 450 Дж. 10*. Увеличилась в 3,2 раза. 11*. 180 кПа. 12*. 750 Дж. 13**. 100 кПа; 1,5 г. 14**. 
. Подсказка: необходимо использовать закон сохранения суммарной кинетической энергии всех молекул в теплоизолированной системе. 15. 1 а: Δ U 12 > 0 (увеличивается), Δ U 23 < 0 (уменьшается), Δ U 31 = 0 (не изменяется); 1б: Δ U 12 > 0; Δ U 23 = 0, Δ U 31 < 0. Подсказка. В случае 1а об изменении внутренней энергии можно судить непосредственно по изменению температуры. В случае 1 б об изменении внутренней энергии можно судить по изменению произведения рV, которое в соответствии с уравнением Менделеева-Клапейрона меняется пропорционально температуре: рV = vRT, при этом надо иметь в виду, что переход 2–3 - изотермический, то есть Т 23 - постоянная величина. 16. Δ U ≈ 499 Дж. 17. Δ U ≈ -25 Дж. 18. Δ U = 600 кДж. 19. ΔU = - 450 кДж. 20**. Г. 
21. А = 200 Дж; А ’= - 200 Дж. 22. А = - 500 Дж; А ’= 500 Дж. 23. А = 400 Дж; Δ Т ≈ 24 К; Δ U = - 600 Дж. Подсказка. Для определения изменения температуры газа необходимо воспользоваться уравнением Менделеева-Клапейрона. 24. А ≈ 665 Дж. Подсказка. Разберите пример 1.
Пример 1. Какую работу совершает 1 моль идеального газа при его изобарном нагревании от 20 оС до 22 оС?
Решение. Поскольку нагревание происходит при постоянном давлении, то имеем право воспользоваться формулой для работы газа в виде: А = р∆V. По условию неизвестны изменение объема ∆ V, а также давление газа. Но все три термодинамических параметра газа взаимосвязаны уравнением Менделеева-Клапейрона. Запишем это уравнение дважды – для начального и конечного состояния газа:
pV 1 = νRT 1 (1)
pV 2 = νRT 2 (2)
Вычтем из левой и правой частей второго уравнения соответствующие части первого уравнения:
р (V 2 – V 1) = νR (T 2 – T 1), или: р∆V = νR ∆T. Но р∆V = А, следовательно, при изобарном процессе работу можно определить по формуле: А = νR ∆T. При заданных условиях, работа газа равна А = 16,6 Дж.
25. А ≈ 33,24 кДж. 26*. Ав/Аа = 14. 27. 12 . 105 Дж; -1,7 . 104 Дж; 0. Подсказка. В случае, изображенном на рисунке 2в, давление меняется прямо пропорционально температуре. Следовательно, это изохорный процесс, то есть объем газа не меняется ∆ V = 0, и газ не совершает работу. 28. А 12 = 0; А 23 = 18 . 105 Дж; А 34 = 0; А 41 = -6 .105Дж; А = 12 . 105 Дж; на участке 4-1; Т 4 ≈ 481 К. 29. 12 . 105 Дж. Подсказка. Процесс не изобарный, следовательно нельзя пользоваться формулой для работы газа в виде А = р∆V. Но можно воспользоваться тем, что работа газа численно равна площади под графиком зависимости р (V), в данном случае - площади трапеции. При расчете площади (работы газа) следите за единицами измерения величин вдоль каждой оси. 30. 600 кДж. Подсказка. График р (V) замкнутый. Следовательно, работа газа равна площади, ограниченной этим графиком, то есть площади треугольника. Знак результирующей работы положительный, так как положительная работа газа (площадь трапеции под переходом 1-2) больше по модулю отрицательной работы газа (площади под переходом 3-1). 31. – 5 . 105 Дж. 32*. 105 Дж; над поршнем и атмосферным воздухом; 5 Дж; увеличилась потенциальная энергия поршня на 5 Дж, увеличилась внутренняя энергия атмосферного воздуха на 105 Дж. Подсказка. Разберите пример 2.
Пример 2.
| Рис. 1 |
| ∆ h |
| S |
| M |
| pS |
| Mg |
| p 0 S |
Решение. Полезно графически представить себе состояние системы в начале и в конце процесса (см. рис. 1).
По условию нагревание газа производится изобарно, то есть давление газа постоянно, поэтому можно воспользоваться формулой для работы газа, которая справедлива лишь при изобарном изменении его объема: А = р∆V. Процесс будет изобарным, если нагревание происходит настолько медленно, что поршень поднимается равномерно. Тогда, согласно второму закону Ньютона, сумма сил действующих на поршень, равна нулю. На поршень действуют силы: сила атмосферного давления p 0 S, вес груза Mg и сила давления газа pS. Следовательно: p 0 S + Mg = pS. То есть:
Изменение объема газа равно: ∆V = S∆h. Таким образом, работа газа будет равна: 
. Подставив числовые значения, получим: А = 50025 Дж.
Возникают вопросы: 1) над какими телами газ совершил данную работу; 2) какие энергетические изменения произошли с этими телами в результате работы газа над ними (работа, совершенная над телом – мера изменения его энергии). Безусловно, газ совершает работу над поршнем с грузом. В результате этой работы потенциальная энергия груза увеличивается: ∆W = Mg∆h = 12,5кг.10м/с2.0,2м = 25 Дж. Следовательно, именно в 25 Дж совершается газом работа над поршнем. Но полная работа газа значительно больше! Многие делают серьезную ошибку, отвечая, что газ совершает работу только над поршнем. Поскольку газ совершает работу и против силы атмосферного давления, то именно над атмосферным воздухом и совершается газом остальная (и в данном случае, основная) работа в 50000 Дж. В результате, именно на 50000 Дж увеличивается внутренняя энергия окружающего воздуха: молекулы воздуха, сталкиваясь с движущимся поршнем приобретают дополнительный импульс, следовательно, и дополнительную кинетическую энергию.
33*. В кинетическую энергию баллончика (если он не закреплен) и кинетическую энергию газовой струи. 34*. 0,22 г. 35*. ∆T ≈ 13 К. Подсказка. Обратите внимание на то, что положительная работа совершена над газом внешними телами. 36**. 324 К; ≈ 0,031 м3. 37**. T = const .V 2; A = 3 PoVo/ 2. Подсказка. Разберите пример 3.
Пример 3. Идеальный газ нагревается так, что температура изменяется прямо пропорционально значению квадрата его давления. Найдите работу, произведенную газом, при увеличении его объема от V 1 до V 2.
Решение. Так как расширение газа происходит при переменном давлении, то мы не можем пользоваться формулой для работы газа при изобарном процессе: А = р∆V. Возможно, удастся использовать тот факт, что работа газа численно равна площади под графиком р (V). Но чтобы построить график р (V), необходимо знать уравнение этой зависимости. Запишем два уравнения, отражающие связь параметров газа в данном процессе:
pV = νRT (1) - уравнение Менделеева-Клапейрона;
Т = αр 2 (2) – по условию задачи, где α - введенный коэффициент пропорциональности между Т и р 2.
Исключим из этих уравнений параметр Т, подставив его значение из уравнения (2) в уравнение (1): pV = νRαр 2. Таким образом: р = V / νRα. Построим интересующий нас график (рис. 2).
| V 1/ vRα |
| V |
| Р |
| V 2 |
| V 1 |
| Рис. 2 |
| V 2/ vRα |
| 0 |
| V |
| Р |
| Рис. 3 |
| 1 |
| 2 |
| 3 |
Фигура под графиком – трапеция, чья площадь, а следовательно, и работа газа равна:
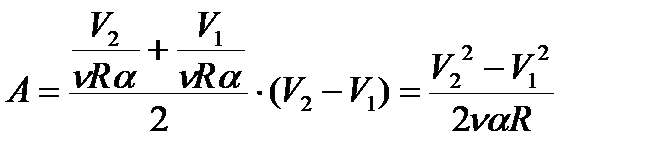
Разумеется, если бы зависимость р (V) оказалась не линейной, то решение было бы более сложным. Во всяком случае, более сложным настолько, насколько Вы не владеете таким математическим действием, как интегрирование.
38**. A = mRα(V22 – V21)/2M. 39**. T = A/R (k - 1). Подсказка. Разберите пример 4.
Пример 4. Состояние моля идеального газа изменялось вначале по изохоре 1-2, а затем по изобаре 2-3 (рис. 3). При этом газом совершена работа А. Известно, что температура в конечном состоянии 3 и в состоянии 1 одинакова и равна Т. Определить отношение давлений в состояниях 1 и 2.
Решение. Переход 1-2 – изохорный. Следовательно, искомое значение отношений давлений равно р 1/ р 2 = Т 1/ Т 2, или (с учетом условия Т 1 = Т):
р 1/ р 2 = Т / Т 2 (1)
Очевидно, необходимо попытаться определить Т 2 через заданное значение работы газа А. Газ совершил работу при изобарном расширении на переходе 2-3 (на участке 1-2 работу газ не совершает, т.к. V = const): А = р 2(V 3 – V 2). Из уравнения Менделеева-Клапейрона для изобарного процесса справедливо: р ∆ V = νR∆T. То есть работа газа на участке 2-3 равна: А = νR (Т 3 – Т 2), или – с учетом условия Т 3 = Т:
А = νR (Т - Т 2)
Из последнего уравнения выразим Т 2: Т 2 = vRT – A. Подставив это значение в уравнение (1), получаем: р 1/ р 2 = Т / (vRT – A), или с учетом условия v = 1:
р 1/ р 2 = Т /(RT – A)
40**. v (Т 1 – Т 2)(Т 1 – Т 0) R / T 1. Подсказка. Обязательно постройте график р (V). 41**. R (
)2. 42. Увеличилась на 7,5 МДж. 43*. 9а: Q 12 > 0, Q 23 > 0, Q 31 < 0, Q > 0; 9б: Q 12 > 0, Q 23 < 0, Q 31 > 0, Q < 0; 9в: Q 12 > 0, Q 23 > 0, Q 31 < 0, Q < 0. Подсказка. Разберите пример 5.
Пример 5. На рисунке 4 изображен циклический процесс, проведенный с газом при неизменной его массе. Опишите характер теплообмена газа при каждом переходе, составляющем цикл. Каков характер теплообмена газа за полный цикл?
| Рис. 5 |
| Р |
| V |
| 2 |
| 1 |
| 3 |
| Рис. 4 |
| Р |
| Т |
| 2 |
| 1 |
| 3 |
Q = ∆A + ∆U (1)
Если правая часть равенства (1) больше нуля, то газ получает тепло, и наоборот: если меньше нуля, то – отдает.
Рассмотрим переход 1-2. Это изобарный процесс, поскольку р 12 = const, и идет с увеличением температуры ∆ Т 12 > 0, следовательно, внутренняя энергия газа увеличивается: ∆ U 12 > 0. При изобарном процессе объем прямо пропорционален температуре. Значит, на этом участке объем так же увеличивается ∆ V 12 > 0, следовательно, газ совершает положительную работу над внешними телами: ∆ А 12 > 0. Таким образом, на участке 1–2 газ получает некоторое количество теплоты Q 12 = ∆ U 12 + ∆ А 12 > 0.
Рассмотрим участок 2–3. Он описывает изотермический процесс, поскольку Т 23 = const (∆ Т 23 = 0). Следовательно, внутренняя энергия газа не изменяется: ∆ U 23 = 0. Давление увеличивается, а поскольку при изотермическом процессе давление газа обратно пропорционально его объему, то на этом участке объем газа уменьшается: ∆ V 23 < 0. Следовательно, А 23 < 0. Таким образом, на участке 2–3 газ отдает некоторое количество теплоты Q 23 = 0 + А 23 < 0.
| Q 31 < 0 |
| - получает тепло |
| на участке 1-2: |
| ∆ Т 12 > 0 ∆ U 12 > 0 ∆ V 12 > 0 ∆ А 12 > 0 |
| Q 12 > 0 |
| - отдает тепло |
| на участке 2-3: |
| ∆ Т 23 = 0 ∆ U 23 = 0 ∆ V 23 < 0 А 23 < 0 ∆ V 12 > 0 ∆ А 12 > 0 на участке 1-2 |
| Q 23 < 0 |
| - отдает тепло |
| на участке 3-1: |
| ∆ V 31 = 0 А 31 = 0 ∆ Т 31 < 0 ∆ U 31 < 0 ∆ V 23 < 0 А 23 < 0 ∆ V 12 > 0 ∆ А 12 > 0 на участке 1-2 |
Каков же характер теплообмена газа за весь цикл? То есть, каков знак суммы Q = Q 12 + Q 23 + Q 31? Ответить на этот вопрос можно, применив первый закон термодинамики сразу ко всему циклу: Q = ∆A + ∆U. Поскольку газ в результате замкнутого цикла из состояния 1 опять вернулся к тому же состоянию 1 с теми же термодинамическими параметрами, то и ∆ Т = 0, следовательно, ∆U = 0 за весь замкнутый цикл, тогда: Q = A – полной работе газа за весь замкнутый цикл.
Полная работа газа за весь цикл численно равна площади фигуры, ограниченной графиком р (V). Вопрос, каков знак этой площади. Построим график зависимости р (V) - рис. 5. Площадь фигуры по модулю равна площади под графиком р (V) на участке 3-2 минус площади фигуры под графиком р (V) на участке 1-2. При этом отметим, что отрицательная работа газа на участке 3-2, где объем уменьшается, больше по модулю положительной работы на участке 1-2, где объем увеличивается: | A 32| > | A 12|. Значит, полная работа газа за весь цикл A = A 32 + A 12 =- | A 32| +| A 12| < 0. Таким образом, за весь цикл Q = А < 0, то есть газ отдает количество теплоты окружающим телам.
44. а) получил 1 МДж; б) отдал 1 МДж. Подсказка. Обратите внимание, что в условии говорится о значении работы не самого газа, а над газом. 45. 665 кДж; 1335 кДж. 46*. 99,7 кДж; 149,6 кДж; 249,3 кДж. 47*. cV/(cV + R); R/(cV + R). Подсказка. При изохорном процессе газ не совершает работы, так как V = const, и поэтому Q = ∆ U = сVv∆T. Поэтому изменение внутренней энергии в любом процессе при изменении температуры на ∆T всегда можно выразить как величину сVv∆T. При изобарном процессе Q = ∆ U + A = ∆ U + p∆V = сVv∆T + vR∆T. 48*. 3 кДж; 4,23 кДж. 49*. В ≈ 2,1 раза; 379 Дж. 50*. ≈ 0,4 м3. 51**. 298 К. 52**. 0,5 α (V 22 – V 12); αсV (V 22 – V 12)/ R. 53**. сV + 0,5 R. 54*. ≈ 77 оС. Подсказка. Разберите пример 6.
Пример 6. Моль идеального газа, первоначально находившийся при нормальных условиях, переводят в состояние с вдвое большим объемом и давлением. Процесс перевода слагается из двух участков – изобары и изохоры. Какое количество теплоты подведено к газу? Молярная теплоемкость газа при постоянном объеме сV = 21 Дж/ (моль . К).
| 3 |
| 2 |
| 1 |
| 2 P 0 |
| P 0 |
| 2 V 0 |
| V 0 |
| V |
| P |
| Рис. 6 |
Q = Q 12 + Q 23
Согласно первому закону термодинамики:
Q 12 = ∆ U 12 + A 12
Q 23 = ∆ U 23 + 0, так как процесс 2-3 - изохорный
При любом процессе изменение внутренней энергии газа равно: ∆ U = сVv ∆ T. При изобарном процессе работа газа равна А = р∆V, а V 2 = 2 V 0, поэтому:
Q 12 = сV (T 2 – T 0) + Р 0(V 2 – V 0) = сV (T 2 – T 0) + Р 0(2 V 0 – V 0) = сV (T 2 – T 0) + Р 0 V 0; Q 23 = сV (T 3 – T 2).
В уравнениях учтено, что v = 1.
Задача сводится к определению значений Т 0, Т 2, Т 3 и Р 0 V 0. Поскольку в начальном состоянии 1 газ находится при нормальных условиях, то Т 0 = 273 К. Температуру газа в конце изобарного процесса 1-2 определим из закона Гей-Люссака: T 2/ T 0 = V 2/ V 0 = 2 V 0/ V 0 = 2. Откуда T 2 = 2 T 0. Произведение Р 0 V 0 = RT 0 в соответствии с уравнением Менделеева-Клапейрона. Таким образом, Q 12 = сV T0 + RT 0 = T 0(сV + R). Для определения Т 3 в состоянии 3 воспользуемся законом Шарля. Так как переход 2 - 3 – изохорный, то: Т 3/ Т 2 = Р 3/ Р 2. Учитывая, что Т 2 = 2 Т 0, Р 2 = Р 0 и Р 3 = 2 Р 0, получаем: Т 3/2 Т 0 = 2 Р 0/ Р 0. Отсюда: Т 3 = 4 Т 0. Таким образом, мы имеем систему уравнений:
| Q = Q 12 + Q 23 Q 12 = сV (T 2 – T 0) + Р 0 V 0 T 2 = 2 T 0 Р 0 V 0 = RT 0 Q 23 = сV (T 3 – T 2) Т 3 = 4 Т 0 |
Решая ее относительно Q, получаем: Q = T 0(3 CV + R) = 20 кДж.
55**. 6 кДж. 56**. В 5/3 раз. Подсказка. Разберите пример 7.
Пример 7. В вакуумном пространстве вертикально стоит цилиндрический сосуд, закрытый сверху подвижным поршнем массы М. Внутри сосуда находится одноатомный газ при давлении р. Внутреннее сечение цилиндра S, а поршень находится на высоте H над его дном. Поршень отпустили. После непродолжительных колебаний он останавливается. На каком расстоянии от начального положения остановится поршень, если теплоемкость газа при постоянном объеме много больше теплоемкости поршня и цилиндра? Вся система теплоизолирована.
Решение. Изобразим на рисунке начальное и конечное состояния системы (рис. 7). Мы предположили, что уровень поршня в конечном состоянии снизится. Для решения задачи можно использовать первый закон термодинамики для газа с учетом того, что процесс изменения его состояния адиабатный (система теплоизолирована): 0 = ∆ U + A, где А – отрицательная работа газа, совершаемая над поршнем при переменном давлении. Но можно использовать закон сохранения энергии для замкнутой системы: газ-поршень-земля (атмосферный воздух исключен по условию). Нулевой
| P1, V1, T1 |
| h |
| Рис. 7 |
| P, V, T |
| H |
| Mgh = 3/2 R (Т 1 – Т) рSH = RT p 1 S (H - h) = RT 1 p 1 = Mg/S |
Решая ее относительно h, получаем: 
.
57**. 2 Р 0 V 0/ T 0. Подсказка. Разберите пример 8.
Пример 8. Состояние одноатомного идеального газа меняется по закону Р = аV, где а – постоянный коэффициент. Определите молярную теплоемкость газа при этом процессе.
Решение. Молярная теплоемкость показывает, какое количество теплоты необходимо, чтобы повысить температуру 1 моля газа на 1 К, и соответственно равна:
Очевидно, необходимо выразить Q через v и ∆ Т, чтобы сократились их значения. В соответствии с первым законом термодинамики количество теплоты, переданное газу, идет не только на повышение его внутренней энергии, но и на совершение газом работы:
Q = ∆ U + A (1)
Поскольку идеальный газ одноатомный, то изменение его внутренней энергии при повышении температуры на ∆Т равно: ∆U = 3/2 Rv∆Т.
| V |
| P |
| P 2 = aV 2 |
| V 2 |
| V 1 |
| P 1 = aV 1 |
| Рис. 8 |
(2)
Выразим значение V 2 через Т газа. С одной стороны при любом процессе выполняется уравнение Менделеева - Клапейрона: РV = vRT. С другой стороны, по условию Р = аV. Из этих двух последних соотношений, исключив переменную Р, получаем: аV 2 = vRT. Используя полученную связь между V и Т, перепишем уравнение (2):
. Таким образом, уравнение (1) можно переписать:
Q = 3/2 Rv∆Т + 1/2 vR∆Т = 2 vR∆T
Тогда молярная теплоемкость газа будет равна:
.
58**. 
R Δ Т – 
Q. Подсказка. Разберите пример 9.
Пример 9. Моль гелия совершает работу величиной А в замкнутом цикле (рис. 9), состоящем из адиабаты 1-2, изотермы 2-3, изобары 3-1. Найти величину работы, совершаемой в изотермическом процессе, если разность максимальной и минимальной температуры газа в цикле равна Δ Т.
| V |
| Р |
| Рис. 9 |
| 1 |
| 2 |
| 3 |
Переход 3-1 изобарный, поэтому А 31 = р Δ V = vR (T 1 – T 3). Но T 3 = T 2, так как точки 3 и 2 лежат на одной изотерме, поэтому А 31 = vR (T 1 – T 2) = vR Δ Т. Таким образом, работа газа в изотермическом процессе равна: А 23 = А - 3/2 vR Δ Т - vR Δ Т.
С учетом v = 1 имеем: А 23= А - 5/2 R Δ Т. 59**. Q = А + 3/2 R Δ Т. 60. 11 %. 61. а) 274 кВт . ч; ≈ 200 кВт . ч. 62*. k Т. 63**. По циклу 1-3-4-1 больше в 23/21 раз. Подсказка. Разберите пример 10.
| 3 |
| 2 |
| 1 |
| V |
| Р |
| Рис. 10 |
| 4 |
Решение. По определению КПД тепловой машины равен: 
, где А – работа, совершенная газом за цикл; QH - количество теплоты, переданное газу (QH > 0) от нагревателя. По условию Т 2 = Т 4 = Т. Проанализируем, на каких переходах газ получает тепло. На изохорном переходе 1-2 температура повышается пропорционально давлению, а работа газом не совершается. Следовательно, на участке 1-2 газ получает тепло (Q 12 > 0): Q 12 = ∆ U 12 = 3/2 Rv (T – Т 1). Здесь учтено, что газ одноатомный, а следовательно, CV = 3/2 R.
На изобарном переходе 2-3 температура газа растет пропорционально повышению объема и, кроме того, газ совершает положительную работу. Следовательно, на участке 2-3 газ получает тепло (Q 23 > 0): Q 23 = ∆ U 23 + А 23 = 3/2 Rv (T – Т 1) + vR (T 3 - T). Здесь учтено, что при изобарном процессе работу газа можно определить как: А = р∆V = vR∆T.
Анализируя аналогично переходы 3-4 и 4-1, приходим к выводу, что на этих участках газ отдает тепло (Q 34 < 0 и Q 41 < 0).
Таким образом, газ за весь цикл получает от нагревателя количество теплоты, равное:
QH = Q 12 + Q 23 = 3/2 Rv (T – Т 1) + 3/2 Rv (T – Т 1) + vR (T 3 - T) = 
(1)
Определим, какую работу совершает газ за весь цикл. Газ совершает работу на изобарном переходе 2-3: А 23 = vR (T 3 - T) > 0 и на изобарном переходе 4-1: А 41 = vR (T1 - T) < 0. Таким образом, работа газа равна: А = А 23 + А 41 = vR (T 3 - T) + vR (T1 - T) = vR (Т 3 – 2 Т + Т 1) (2)
В выражении для Q и для А неизвестной величиной является температура Т в состояниях 2 и 3. На переходах 1-2 и 3-4 по закону Шарля для изохорного процесса справедливо: 
; 
. Здесь учтено, что р 2 = р 3 и р 1 = р 4. Тогда: 
. Отсюда следует, что 
. Подставим найденное значение Т в уравнения (1) и (2): 
; 
Таким образом, КПД цикла равен: 
. Самое главное в подобных задачах:
1) понимать, что поиск КПД тепловой машины можно искать по формулам:
- важно сделать наиболее рациональный выбор, исходя из условий задачи.
2) выразить числитель и знаменатель через одни и те же физические величины, так как в результате должна получиться безразмерная величина.
64**. А (1 – η)/ η. 65**.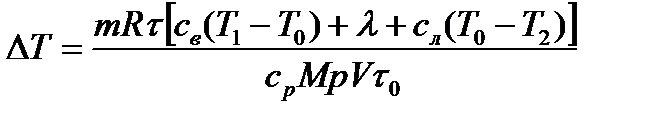 
. Подсказка. Поскольку охлаждение воды начинается с Т 1 = 293 К, то очевидно, это и есть комнатная температура, то есть температура нагревателя. Лед охлаждается до температуры Т 2 = 271 К – это и есть температура холодильника. Нагревание воздуха в комнате происходит при атмосферном давлении, которое можно взять равным 100 кПа. Разберите пример 11.
Пример 11. Идеальная машина, работающая по обратному циклу Карно, передает тепло от холодильника с водой при температуре Т 1 = 0 оС кипятильнику с водой при температуре Т 2 = 100 оС. Сколько воды нужно заморозить в холодильнике, чтобы превратить в пар mп = 1 кг воды в кипятильнике?
Решение. Прежде всего, необходимо разобраться, каковы температуры нагревателя и холодильника тепловой машины. Очевидно, температура холодильника равна температуре замерзающей воды, то есть Т 1 = 0 оС. Температура нагревателя равна температуре кипящей воды Т 2 = 100 оС. Поскольку тепловая машина идеальная, работающая по циклу Карно, то его КПД равен: 
. С другой стороны, как у любой тепловой машины КПД так же равен: 
. Но, поскольку машина работает по обратному циклу (то есть как холодильная машина), то Q 2 < 0 – тепло, передаваемое нагревателю, то есть в нашем случае кипящей воде; Q 1 > 0 – тепло, отбираемое у холодильника, то есть у льда. (Напомним, что при работе машины по прямому циклу Q 2 > 0– рабочее тело забирает у нагревателя, Q 1 < 0 – отдает холодильнику). Тепло, выделяемое при замерзании воды и отбираемое машиной, равно: Q 1 = λ mл; тепло передаваемое нагревателю тратится на парообразование воды: Q 2 = Lmп. Таким образом, мы имеем систему уравнений:
 
Q 1 = λ mл
Q 2 = Lmп
|
Решая систему относительно искомой величины mл, получаем результат:
= 5 кг.
66. 153,7 МДж. 67. 557 кДж. 68. 2,2 кДж/(кг.К). Подсказка. Разберите пример 12.
Пример 12. В калориметр с теплоемкостью С = 60 Дж/К было налито воды массой m 1 = 200 г при температуре t 1 = 80 оС. В воду опустили кусочек льда массой m 2 = 50 г с начальной температурой t 2 = – 10 оС. Каково значение установившейся температуры системы?
Решение. В задачах, в которых идет речь о теплообмене тел, важно ответить на следующие вопросы.
Вопрос первый. Сколько тел участвуют в теплообмене? В данном случае – три тела: лед, вода и калориметр (так как задана его теплоемкость). Хотя конечно, окружающие тела так же участвуют в теплообмене, например, воздух и подставка под калориметром. Но калориметр имеет плохую теплопроводность, поэтому отдачей тепла окружающим телам можно пренебречь, тем более, что в условии задачи нам ничего неизвестно об окружающих телах. Поэтому будем считать, что система тел: калориметр – вода – лед – теплоизолированная система.
Вопрос второй. Какие тела отдают часть своей внутренней энергии (выделяют количество теплоты), а какие - приобретают (поглощают количество теплоты). В данном случае, очевидно, выделяют количество теплоты более нагретые вода и калориметр (справедливо полагать, что начальные температуры воды и калориметра одинаковы), а лед – поглощает как менее нагретое тело. В соответствии с законом сохранения энергии, выделенное количество теплоты одной частью тел равно поглощенному количеству теплоты другой частью тел теплоизолированной системы при условии, что тела в системе не производят механической работы: | Q воды| + | Q калорим| = Q льда (1).
Вопрос третий. К какому конечному результату вероятнее всего приведет процесс теплообмена между телами системы. Почему «вероятнее всего»? Дело в том, что результат теплообмена не всегда очевиден. Например, в нашем случае конечная температура системы может оказаться ниже нуля, если вся вода охладится до 0 оС, закристаллизуется и охладится до более низкой общей температуры системы. Но температура системы может оказаться и выше нуля, если лед нагреется до 0 оС, растает и нагреется до общей температуры системы. Поэтому важно проанализировать начальные параметры системы, чтобы предугадать наиболее вероятный результат теплообмена. По условиям задачи масса воды 200 г существенно больше, чем масса льда 50 г, да и начальная температура воды 80 оС существенно дальше отстоит от температуры ее кристаллизации 0 оС, чем начальная температура льда от температуры плавления. Вероятнее всего, конечная температура системы будет выше 0 оС.
Вопрос четвертый. Какие тепловые процессы происходят с телами в результате теплообмена? Если конечная температура системы будет выше 0 оС, становиться ясно, что вода и калориметр просто охладятся до конечной температуры, а лед, во-первых, охладиться до 0 оС, во-вторых, расплавиться при 0 оС, в-третьих, нагреется до конечной температуры, будучи уже в жидком состоянии.
Схематично, все ответы на поставленные вопросы изображены на рисунке 11.
| Рис. 11 |
| Выделяют количество теплоты |
| вода |
| калориметр |
| t 1 |
| t к |
| Q 1 |
| t 1 |
| t к |
| Q 2 |
| Поглощает количество теплоты |
| лед |
| t 2 |
| Q 3 |
| t пл |
| t к |
| Q 5 |
| t пл |
| Q 4 |
Тогда в уравнении теплового баланса с одной стороны будут стоять две порции количества теплоты, описывающие его выделение в результате охлаждения двух тел. С правой стороны будут стоять три порции количества теплоты, описывающие его поглощение одним и тем же телом в результате трех последовательных тепловых процессов, происходящих с этим телом: | Q 1| + | Q 2| = Q 3 + Q 4 + Q 5 (2). Осталось расписать формулы расчета каждой порции количества теплоты. Необходимо отметить, что уравнение (2) записано в таком виде, при котором все порции Q берутся по модулю. Итак:
Q 1 = c в m 1(t 1 – t к) – количество теплоты, выделяемое водой при ее охлаждении от температуры t 1 до конечной температуры t к. Здесь из большего значения температуры t 1 отнимается меньшее значение t к (мы определяем модуль Q).
Q 2 = C (t 1 – t к) - количество теплоты, выделяемое калориметром при его охлаждении от температуры t 1 до конечной температуры t к. Здесь необходимо помнить, что С – это не удельная теплоемкость вещества, из которого изготовлен калориметр (тепловая характеристика 1 кг вещества), а теплоемкость тела - калориметра (тепловая характеристика всего тела). Теплоемкость тела равна количеству теплоты, которое необходимо сообщить всему телу для нагревания его на 1 оС (на 1 К);
Q 3 = cлm2 (t пл – t 2) - количество теплоты, поглощаемое льдом при его нагревании от температуры t 2 до температуры плавления t пл.
Q 4 = λm2 - количество теплоты, поглощаемое льдом при его плавлении, которое происходит при одной и той же температуре плавления.
Q 5 = cлm2 (t к – t пл) - количество теплоты, поглощаемое водой, образовавшейся при плавлении льда, при ее нагревании от температуры плавления t пл до конечной температуры t к системы. Подставим все расшифрованные значения порций количества теплоты в уравнение (2):
c в m 1(t 1 – t к) + C (t 1 – t к) = cлm2 (t пл – t 2) + λm2 + cлm2 (t к – t пл) (3)
В уравнении (3) одна неизвестная величина – конечная температура t к. Решим это уравнение относительно неизвестной величины:
Осталось подставить числовые значения, взяв их в единицах системы СИ. Правда, размерность температуры совсем не обязательно брать в единицах системы СИ (в Кельвинах), так как в уравнении (3) везде идет речь об изменении температуры, а поскольку цены деления шкалы Цельсия и шкалы Кельвина совпадают, то изменение температуры так же будут иметь одинаковые значения по обеим шкалам.
≈ 47 (оС)
69. 22 кг. Подсказка. В этой задаче система тел: дрова – снег – не является теплоизолированной. Необходимо учесть, что снег поглощает количество теплоты Q с, составляющее лишь 40 % от того количества теплоты Q д, которое выделяется при сгорании дров. Остальные 60 % поглощают окружающие тела (сосуд, в котором находится снег, окружающий воздух, опора под дровами и т.п.). С учетом этого уравнение теплового баланса будет записано: Q с = 0,4 Q д. Далее необходимо уточнить, из какого количества слагаемых будет состоять левая часть уравнения (исходя из ответа на вопрос: какие тепловые процессы будут происходить со снегом). 70*. 33,4 оС. 71. Нет, так как из-за теплообмена между каплей воды и массивным по сравнению с массой воды термометром погрешность измерения будет слишком велика (см. предыдущую задачу). 72. 89 оС. 73*. 55 оС. Подсказка. Эта задача типа «2 в 1». Решение этой задачи представляет собой описание с помощью уравнения теплового баланса двух этапов теплообмена: теплообмен в системе «вода – первое тело» и теплообмен в системе «вода – первое тело – второе тело». При этом необходимо понимать, что конечная температура воды и первого тела в результате первого этапа теплообмена являются одновременно начальной температурой при втором этапе теплообмена. Но в полученных двух уравнениях будут три неизвестные величины: масса воды, масса тела и конечная искомая температура. Тут вам необходимо вспомнить математические приемы, позволяющие комбинировать две неизвестные величины в одну. 74*. 23 г. Подсказка. Обратите внимание на выражение «мокрый снег». Оно означает, что вода в комке состоит частично из кристаллической фазы, а частично из жидкой фазы. При какой температуре это возможно? 75*. 0 оС; 400 г воды и 300 г льда. Подсказка. Анализируя начальные параметры системы, необходимо обратить внимание на то, что массы льда в 2,5 раза больше, чем воды. При таких условиях трудно с большой вероятностью предугадать результат теплообмена: то ли конечная температура будет ниже нуля (температуры плавления льда), то ли она будет выше нуля. В таких случаях разумно сделать предварительный расчетный анализ: рассчитайте, какое количество теплоты Q 1 выделилось бы, если бы вся вода
