При анализе и синтезе больших систем получил развитие системный подход, который отличается от классического (иначе - индуктивного) подхода.
При классическом подходе рассматривается система путей перехода от частного к общему и синтезируется (конструируется) система путем слияния ее компонент, разрабатываемых раздельно.
Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель, причем исследуемый объект выделяется из окружающей среды.
Независимо от типа модели при ее построении необходимо руководствоваться рядом принципов системного подхода:
1) пропорционально-последовательное продвижение по этапам и направлениям создания модели;
2) согласование информационных, ресурсных, надежностных и др. характеристик;
3) правильное соотношение отдельных уровней иерархии в системе;
4) цельность отдельных обособленных стадий построения модели.
2.1.1. Структура системы – совокупность связей между элементами системы
Можно выделить различные подходы к исследованию структуры системы с ее свойствами:
- структурный;
- функциональный.
При структурном подходе выявляются:
- состав выделенных элементов;
- связи между ними.
Структура система в зависимости от цели может быть описана на разных уровнях рассмотрения.
Наиболее общее описание структуры – это топологическое, позволяющее определить в самых общих понятиях составные части системы и хорошо формализуемое на базе теории графов.
Менее общим является функциональное описание, когда рассматривается отдельные функции, т.е. алгоритмы поведения системы.
При наличии некоторого эталона сравнения можно ввести количественные и качественные характеристики систем.
Для количественной характеристики вводятся числа, выражающие отношение между данной характеристикой и эталоном.
Качественные характеристики системы находятся, например, с помощью метода экспериментальных оценок.
Качество функционирования системы S определяется показателем эффективности, который является значением критерия оценки эффективности.
Система S может оцениваться либо совокупностью частных критериев, либо некоторым общим интегральным критерием.
Создаваемая модель M с точки зрения системного подхода также является системой S’ = S’ (M) и может рассматриваться по отношению к внешней среде E: М’ = М’ (S,E).
2.1.2. Экспериментальные исследования систем
Основным критерием любой теории является практика, и даже сугубо математические науки базируются на фундаменте практических знаний.
Одновременно с развитием теории и методов анализа и синтеза совершенствуются и методы экспериментального изучения реальных объектов.
Моделирование базируется на некоторой аналогии реального и мысленного эксперимента.
Аналогия – основа для объяснения изучаемого явления. Однако критерием истины может служить только практика, только опыт.
Эксперимент – это некоторая процедура организации и наблюдения каких-то явлений, которые осуществляются в условиях, близких к естественны, либо имитируют их.
Различают пассивный эксперимент, когда исследователь наблюдает протекающий процесс, и активный, когда вмешивается и организует протекание процесса.
Стадии разработки моделей
Существуют две основные стадии:
- макропроектировние;
- микропроектирование.
На стадии макропроектирования на основе данных о реальной системы S и внешней среде E:
- строится модель внешней среды;
- выявляются ресурсы и ограничения;
- выбирается критерий адекватности модели M реальной системе S.
В процессе моделирования выбирается оптимальная стратегия управления.
Стадия микропроектирования зависит от типа выбранной модели. На этой стадии можно установить основные характеристики созданной модели, оценить время работы сетей и затраты для получения заданного качества соответствия модели процессу функционирования системы S.
Понятие подобия
2.3.1. Общие положения
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же [9, 16].
При моделировании абсолютное подобие отсутствует, и это приводит к тому, что приходится ограничиваться тем требованием, чтобы созданная модель достаточно хорошо отражала лишь какие-то отдельные стороны функционирования объекта.
Характеристики объектов или их отдельных элементов можно определить как теоретически, так и экспериментально.
Теоретические методы основаны на использовании полной системы уравнений.
При проведении экспериментов для проверки результатов теоретических исследований не всегда удается применить реальный объект. Поэтому эксперименты проводятся на модели.
В связи с этим возникает вопрос о возможности переноса полученных на модели экспериментальных результатов на реальные объекты.
Ответ на этот вопрос дает теория размерности и подобия, которая:
- устанавливает условия, которые должны соблюдаться в опытах с моделями;
- выделяет характерные и удобные параметры, определяющие основные свойства объекта.
При изучении механических явлений вводится ряд понятий, например, энергии, скорости, напряжения и т.п., которые характеризуют рассматриваемое явление и могут быть заданы и определены с помощью чисел.
Все вопросы о движении и равновесии формируются как задачи об определении некоторых функций и числовых значений для величин, характеризующих явление. Причем при решении таких задач законы природы и различные геометрические соотношения представляют в виде функциональных уравнений – обычно дифференциальных.
При исследованиях эти уравнения служат для:
- установления общих качественных свойств движений и
- фактического вычисления искомых функциональных связей с помощью различных математических операций.
Однако механическое исследование не всегда возможно осуществить путем математических рассуждений и вычислений.
В ряде случаев решение механических задач встречается с неопределенными математическими трудностями.
Очень часто мы не имеем вообще математической постановки задачи, т.к. исследуемое явление настолько сложно, что для него пока еще нет удовлетворительной схемы и нет уравнения движения (например, с этим встречаются в области авиамеханики, гидромеханики, в проблемах изучения прочности и деформаций различных конструкций ит.п.).
В этих случаях главную роль играют экспериментальные методы исследования, которые дают возможность установить простейшие опытные факты, на основе которых можно формировать законы, управляющие исследуемым явлением, и записать их в виде математических соотношений.
Для правильной постановки и обработки экспериментов, результаты которых позволяли бы установить общие закономерности и могли бы быть приложенными к случаям, в которых эксперимент не проводился непосредственно, необходимо давать общий качественный анализ.
Кроме того, сама постановка экспериментов, результаты которых представляются в виде совокупности чисел, может осуществляться только на основе предварительного теоретического анализа.
В постановке опытов очень важно правильно выбрать безразмерные параметры. Число их должно быть минимальным, и взятые параметры должны отражать в наиболее удобной форме основные эффекты.
Возможность такого предварительного качественного теоретического анализа и выбора системы определяющих безразмерных параметров дает теория размерности и подобия.
2.3.2. Основные понятия теории размерности
Размерные и безразмерные величины
Величины, числовые значения которых зависят от принятых масштабов, т.е. от системы единиц измерения, называются размерными величинами.
Величины, числовые значения которых не зависят от системы единиц измерения, называются безразмерными величинами.
Примеры:
- длина, время, сила, энергия, момент силы и т.д. – размерные величины;
- углы, отношение двух длин, отношение квадратов длины к площади, отношение энергии к моменту силы и т.п. - безразмерные величины.
Основные и производные единицы измерения
Различные физические величины связаны между собой определенными соотношениями.
Поэтому если некоторые из этих величин принять за основные и установить для них какие – то единицы измерения, то единицы измерения всех остальных величин будут определенным образом выражаться через единицы измерения основных величин.
Принятые для основных величин единицы измерения называются основными, а все остальные – производными.
На практике достаточно установить единицы измерения для 3 (трех) величин, каких именно – зависит от конкретных условий задачи.
Так в физических исследованиях удобны единицы:
- длины;
- времени;
- массы;
в технике:
- длина;
- время;
- сила.
В системе СИ (с 1963 г. в СССР) за основные величины приняты:
- механические единицы измерения: - метр;
- килограмм;
- секунда;
- единицы силы тока - ампер;
- единица термодинамической температуры – кельвин (К);
- силы света – кандела;
- количества вещества - моль.
После установления основных единиц измерения единицы измерения для других механических величин получаются автоматически.
Выражение производной единицы измерения через основные единицы измерения называется размерностью.
Критерии подобия можно получить из теории размерности.
Размерность данной физической величины определяется соотношением между нею и теми физическими величинами, которые приняты за основные.
В каждой системе единиц имеются свои основные единицы.
Размерность производных единиц принимается на основе физических законов, устанавливающих связь между этими единицами. Эта связь может быть представлена в виде формулы, называемой формулой размерности.
Таблица. Символы единиц измерения и формулы размерности
| Единицы измерения | Формулы размерности (символы и выражения) | Примечания |
| Длина | L | Основные единицы |
| Масса | M | |
| Время | T | |
| Площадь | S = L2 | Производные |
| Скорость | V = L/T | |
| Сила | F = ML/T2 |
Для обозначения размерности какой-либо величины а используется символ [ а ].
Например, для размерности силы F в физической системеобозначают:
[F] = ML/T2.
Теория размерности основана на двух положениях:
1). Отношение двух численных значений какой-нибудь производной величины не зависит от выбора масштабов для основных единиц измерения. (Например, отношение двух площадей не зависит от того, в каких единицах будут измеряться площади).
2). Всякое соотношение между размерными величинами можно сформулировать как соотношение между безразмерными величинами (это положение в теории размерности называют П-теоремой).
Из первого положения следует, что формулы размерности должны иметь вид степенных одночленов, т.е.
,
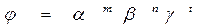где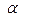 
, 
, 
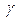- размерности основных единиц.
Пример.
Установить зависимость коэффициента лобового сопротивления тела, обтекаемого газовым потоком (воздухом) сx от основных показателей, входящего в выражение
.
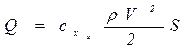Допустим, что сx зависит от размерных величин:
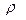- плотности газа;
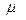- вязкости газа;
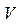- скорости полета;
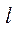- линейного размера тела.
Тогда справедливо:
.
Пользуясь формулой размерности, можно найти безразмерные комбинации указанных физических величин, представив их размерности степенным одночленом
.
Для нахождения показателей a, d, c, n подставим в эту формулу значения размерностей физических величин, например, в системе СИ.
Тогда
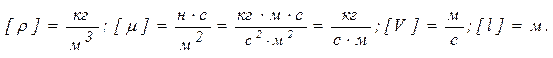
Подставив эти величины в степенной одночлен, получим
.
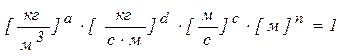Отсюда относительно основных единиц измерения имеем три следующих уравнения:
Решим эти уравнения, считая один из показателей, например, n, известным. Получим
.
Следовательно, коэффициент сx при малых скоростях зависит от числа Re. Показатель степени Re можно найти из эксперимента или каких-либо дополнительных данных о механизме сопротивления тела.
По теории подобия в подобных газовых потоках одинаковы аэродинамические коэффициенты. В частности, для полной аэродинамической силы R при полном подобии имеет место
.
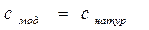Проведя эксперимент, в подобных условиях, результаты моделирования можно переносить на натуру. Поскольку полное подобие практически неосуществимо, то аэродинамические характеристики, определенные в лабораторных условиях, лишь приближенно равны соответствующим характеристикам объекта.
Очевидно, что наиболее достоверные результаты могут дать лишь натурные испытания.
В большинстве случаев моделирование основано на рассмотрении физически подобных явлений.
Механическое или вообще физическое подобие можно рассматривать как обобщение геометрического подобия.
Как известно еще из курса школьной программы по математике, две геометрические фигуры подобны, если отношения всех соответствующих длин одинаковы.
При этом если известен коэффициент подобия (масштаб), то простым умножением на масштаб размеров одной геометрической фигуры получаются размеры другой, ей подобной геометрической фигуры.
Существуют различные способы определения механического или физического подобия.
Два явления подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы к другой.
При этом для осуществления пересчета необходимо знать всего лишь переходные масштабы.
Числовые характеристики для двух различных, но подобных явлений можно рассматривать как числовые характеристики одного и того же явления, выраженные в различной системе единиц измерения.
Для всякой совокупности подобных явлений все безразмерные характеристики (безразмерные комбинации из размерных величин) имеют одинаковые числовые значения. Эти комбинации называются критериями подобия.
Обратное заключение также справедливо: если все безразмерные характеристики для двух движений (явлений) одинаковы, то движения (явления) подобны.
Таким образом, необходимым и достаточным условием подобия двух явлений будет постоянство числовых значений безразмерных комбинаций, образующих базу, т.е. систему безразмерных величин, которые определяют собой все остальные величины.
2.3.3. Примеры подобия
1. Задача об установившемся поступательном плоскопараллельном движении тела в несжимаемой вязкой жидкости.
Все безразмерные величины для такого случая определяются двумя параметрами: углом атаки α и числом Рейнольдса Re.
При этом условие физического подобия – критерии подобия - представляются соотношениями
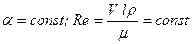. (2.1)
При моделировании этого явления результаты опытов с моделью можно переносить на натуру только для одинаковых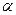 
и 
.
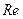Первое условие на практике всегда легко осуществить.
Труднее удовлетворить условие второе: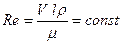 
, особенно в тех случаях, когда обтекаемое тело имеет большие размеры.
Если модель меньше натуры (
), то для сохранения 
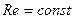необходимо:
- либо увеличить скорость 
, что на практике неосуществимо;
- либо существенно изменить плотность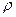 
(увеличить) и вязкость 
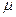(уменьшить).
На практике для обеспечения условия 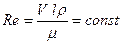сталкиваются с большими трудностями, что выражается в необходимости построения:
- гигантских аэродинамических труб, в которых можно производить продувки самолетов в натуру;
- а также труб закрытого типа, в которых циркулирует с большой скоростью сжатый, т.е. более плотный воздух (с большой ).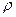
2. Задача исследования механического сооружения из однородного материала, например, мостовой фермы.
Рассмотрим геометрически подобные конструкции – натуру и модель. Составим таблицу определяющих параметров для описания такой конструкции.
Такими являются следующие параметры.
1). Характерный размер конструкции B [м].
2). Если вес конструкции существен, то удельный вес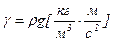 
3). Внешние нагрузки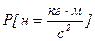 
, действующие на конструкцию.
4). Модуль Юнга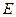 
.
Он используется для определения деформации тела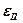 
в направлении действия силы и входит в соответствующее выражение
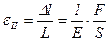, (2.2)
в котором 
- сила, а 
- площадь поперечного сечения. Поскольку деформация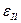 
, как следует из соотношения 
, является безразмерной величиной, то из приведенного выражения (2) вытекает размерность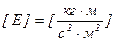 
.
5). Безразмерный коэффициент Пуассона 
, используемый для определения деформации в направлении, перпендикулярном направлению действия силы
. (2.3)
Таким образом, количество определяющих параметров равно 5.
Для этих 5 параметров для механически подобных состояний упругого равновесия существуют 3 параметра - безразмерные комбинации – база. Такую базу в данном случае составляют:
, 
, 
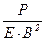. (2.4)
Критерий подобия заключается в равенстве этих параметров на модели и в натуре, т.е.
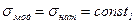; (2.5)
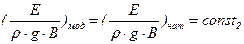; (2.6)
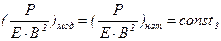. (2.7)
Если модель в n раз меньше натуры, то и на модели деформации (перемещения) будут в n раз меньше, чем в натуре.
Рассмотрим первый случай, когда модель и реальное сооружение состоят из одного и того же материала.
В этом случае из приведенных выше определяющих параметров одинаковыми являются 
, 
, .
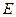Поэтому из второго выражения из (6) следует, для механического подобия необходимо выполнение
. (2.8)
Очевидно, что в условиях исследования обычно имеет место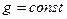 
. Отсюда следует, что должно быть 
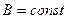, т.е. модель должна совпадать с натурой и, следовательно, при 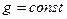моделирование невозможно, т.е. получаемые на модели результатам нельзя распространить на натуру.
Для этого необходимо изменить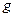 
.
Этого можно добиться искусственным путем, если заставить модель вращаться с постоянной угловой скоростью Ω, поместив ее на так называемую центробежную машину (центрифугу, см. рисунок).
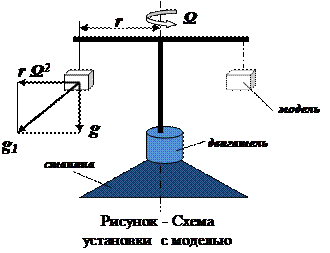При достаточно малых размерах модели и большом радиусе r центробежные силы инерции элементов модели rΩ2 можно считать параллельными.
Вращая вокруг вертикальной оси установку, получим, что в состоянии относительного равновесия модели (по отношению к центробежной машине) на модель будут действовать постоянные массовые силы, аналогичные силе тяжести, но только с другим ускорением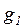 
. При этом из условия обеспечения соотношения (8) вытекает, что требуемая величина 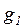обратно пропорциональна характерному линейному размеру модели 
: 
.
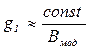Выбором угловой скорости вращения установки Ω можно получить любые большие значения для ускорения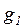
Рассмотрим второй случай, когда внешняя нагрузка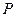 
велика, а собственный вес конструкции мал, что им можно пренебречь. В этом случае параметр 
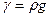несуществен. Тогда условие подобия представляется только двумя критериями (см. (5) и (7)): (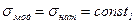) и .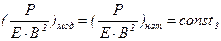
Отсюда следует, что при моделировании с сохранением свойств материала внешние нагрузки необходимо изменять пропорционально квадрату линейных размеров: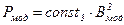 
.
Из теории размерностей и подобия следует, что необходимым и достаточным условием подобия является постоянство числовых значений безразмерных комбинаций, образующих систему безразмерных величин, определяющих остальные параметры свойств объекта.
Эти безразмерные комбинации называются критериями подобия.
Пример.
Сила лобового сопротивления, действующего на тело при обтекании его газовым потоком, определяется зависимостью:
Q = cx q S,
где cx - коэффициент сопротивления;
q – скоростной напор потока;
S – характерная площадь тела.
Коэффициент сопротивления тела cx зависит от 7 параметров
cx = cx(V, p, r, m, cp, cu, L),
где V - скорость воздушного потока ;
p – давление газа в потоке;
r - плотность газа;
m - вязкость;
cp, cn - удельные теплоемкости газа;
L - характерный линейный размер тела.
Поскольку коэффициент cx является безразмерной величиной, то под знаком функции должны быть также безразмерные параметры.
Из общих соображений метода размерности следует, что 7 размерных аргументов функции cx можно свести к 3 аргументам, которые представляют собой безразмерные комбинации параметров V, p, r, m, cp, cu, L, т.к. имеются 4 независимые единицы измерения – масса, длина, время и температура.
Эти безразмерные комбинации (критерии подобия) имеют вид:
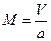
- число Маха, (здесь а – скорость звука);
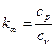- число Рейнольдса;
- показатель адиабаты.
Отсюда следует, что
cx = cx(M, Re, k¥).
Эти критерии имеют физический смысл.
Известно выражение
a2=dp/dr,
где a – скорость звука;
p – давление;
ρ - плотность.
Из приведенного выражения следует, что скорость звука можно рассматривать как параметр, зависящий от свойств сжимаемости, т.е. способности газа изменять плотность с изменением давления. Следовательно, число Маха M характеризует величину воздействия сжимаемости на течение газа.
Число Рейнольдса Re характеризует воздействие вязкости на движущийся газ.
Параметр k¥ определяет особенности течения, обусловленные термодинамическими свойствами газа.
