|
Надамо нормальним рівнянням відповідного вигляду, враховуючи значен
ня коефіцієнтів табл. ІІ.8.2 і те, що- = St, a[St ] = L:
|
(ІІ.8.51)
Розв'яжемо систему (ІІ.8.51) відносно невідомих корелат:
Розділ II
|
(И.8.52) (ІІ.8.53)
Залишається знайти шукані поправки в кути v; та в лінії со;. Скористаємося уже відомою формулою (II.8.45):
|
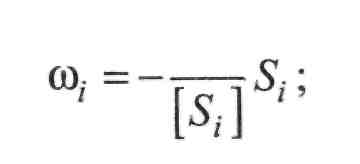
Значення коефіцієнтів 6, і с, візьмемо з табл. II.8.2. Отримаємо: • для ліній:
t
(II. 8.54)
для кутів:
|
(ІІ.8.55)
Виправивши лінії та кути відповідними поправками, знайдемо ймовірніші координати пунктів ходу. Приклад зрівноваження витягнутого полігономет-ричного ходу буде подано в п. П.8.8.
//. 8.7. Строге зрівноваження витягнутого рівностороннього полігонометричного ходу
Поправки в лінії обчислюють за простою формулою:
| (ІІ.8.56) |
|
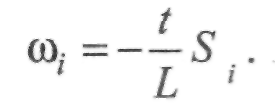
Оскільки — —с - стала величина для цього ходу, а лінії рівні, то поправки
Li
в лінії будуть однаковими:
(П.8.57)
Проте для обчислення поправок v(- в кути необхідно знати абсциси точок
ходу відносно центра ваги ходу £; та суму їхніх квадратів Јj.
Розглянемо, як зміниться формула (II.8.55) для рівностороннього ходу. Візьмемо для простоти хід із парною кількістю сторін п. Це буде справедливим
Планові геодезичні мережі
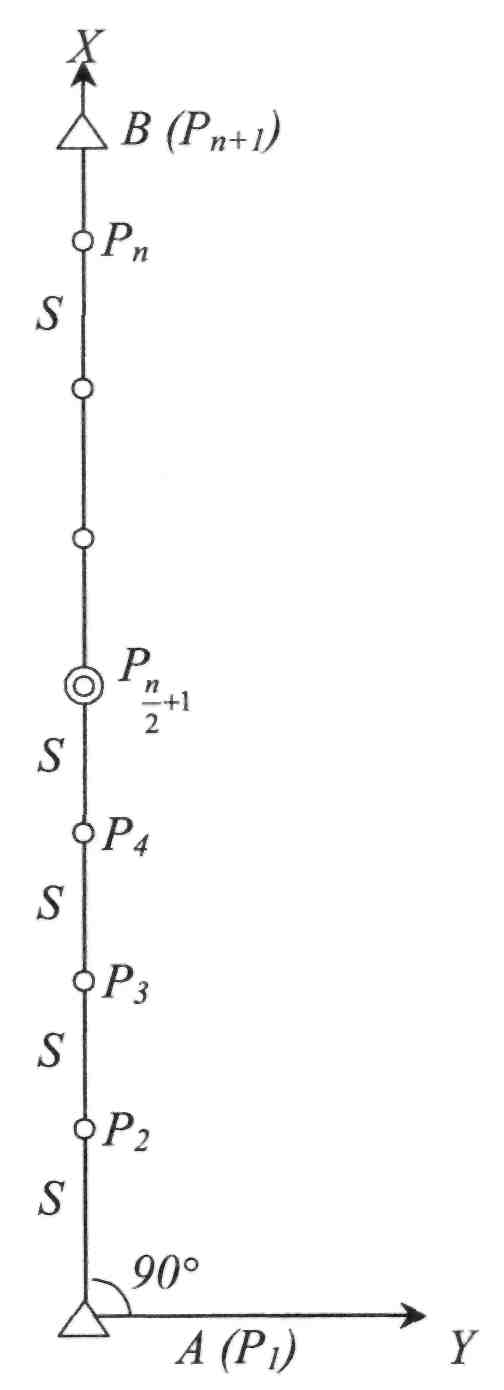
і для непарної кількості сторін. Спрямуємо вісь X уздовж ходу і за початок координат приймемо першу точку (рис. П.8.5).
Тоді: Xl = 0; X2=S; Х3 = 2 S. Отже, для будь-якої точки і маємо:
(ІІ.8.58)
| (П.8.59) (П.8.60) |
|
Центральну абсцису знайдемо за формулою
|
|
Визначимо абсцису точок 
ходу відносно центра ваги: або:
|
(П.8.61)
Розглянемо далі, як зміниться CM - Спочатку
|
знайдемо на основі (И.8.61) значення усіх C,t. Маємо:
(П.8.62)
Такими самими за абсолютним значенням будуть абсциси для другої половини точок ходу, тільки
| Рис. 11.8.5. До зрівноваження витягнутого рівностороннього ходу полігонометрії |
|
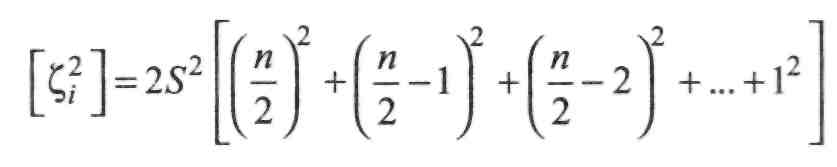
| . (П.8.63) |
зі знаком "плюс". Тому £,- можна подати так:
Розділ II
У квадратних дужках сума квадратів натурального ряду чисел від — до 1.
Як відомо, для такого ряду з п чисел справедлива формула
(II. 8.64)
п Для і—— маємо (помноживши і поділивши на 2 п):
|
|
|
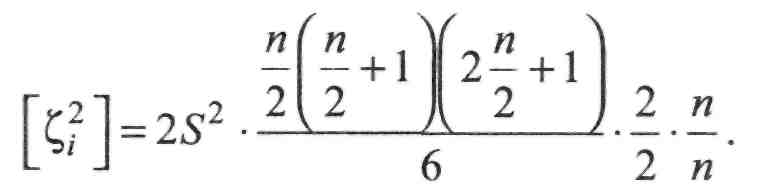
Після перетворень
Отже,
(ІІ.8.65) (ІІ.8.66)
Враховуючи, що S ■ п - L, а також позначивши:
(П.8.67)
отримаємо для поправок 
у кути просту формулу
(П.8.68)
Зауважимо, що bt є функцією тільки кількості сторін ходу п та номера сторони ходуг. Професором А.С. Чеботарьовим складено таблиці bt =/(«,/). Під час обчислення поправок у кути значення Z>, вибирають з цих таблиць.
Отже, зрівноваження витягнутого рівностороннього ходу (майже рівно-стороннього) значно спрощується.
11.8.8. Приклад зрівноваження витягнутого полігонометричного ходу корелатним методом (способом найменших квадратів)
Для кращого розуміння зрівноваження витягнутого полігонометричного ходу, описаного у п. ІІ.8.6, наведемо приклад такого зрівноваження. Використовується відомість обчислення координат, в останньому стовпчику якої подано робочі формули та виконано допоміжні обчислення.
Планові геодезичні мережі
У вертикальній графі 1 виписані номери відомих та тільки що закладених пунктів, координати яких треба визначити.
У графі 2 записані виміряні кути, зокрема і прилеглі. Нев'язка в ході виявилась такою, що дорівнює 
, за допустимої. 
Ця нев'язка
майже порівну розподілена у виміряні кути з оберненим знаком. Поправки величиною 2", або 3" записані зверху над виміряними кутами. Внизу, під виміряними кутами, записані вторинні поправки, поки що невідомі. Щоб позбутися двох поправок на кожний кут, можна у графу 2 записати кути, уже виправлені первинними поправками, або доповнити відомість ще одною вертикальною графою.
Далі переходимо до обчислення дирекційних кутів, використовуючи кути, виправлені первинними поправками. Дирекційні кути записуємо у графу 3. Початковий дирекційний кут ап = 101°38'46" і кінцевий ак = 329°36'29", як задані, уже повинні бути записані у відомість (у графу 3). Так само в графах 10 та 11 повинні бути записані координати початкової (№ 38) та кінцевої (№ 40) точок:
Контролем правильності обчислень дирекційних кутів є формула
Тобто, послідовно обчислюючи дирекційні кути усіх ліній, використовуючи спочатку а„ - початковий дирекційний кут сх37-28 = Ю1°38'46" (наприклад, 
і, дійшовши до
кінцевого дирекційного кута 
, ми повинні отримати
точно кінцевий дирекційний кут оск, тому що кутова нев'язка вже врахована.
У графу 4 записують виміряні лінії. Графу 5 поки що пропускаємо. А далі виконуються обчислення наближених приростів координат за виміряними лініями S та дирекційними кутами, що подані у графі 3.
Обчислені значення Дх та Лу записують у графах 6 та 7. Розраховуються
нев'язки fx та / і записують їх унизу відомості. Використовують, зазвичай, формули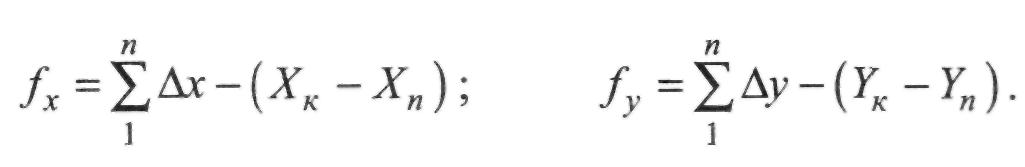 
Далі графи 8 і 9 та 10 і 11 поки що не заповнюються.
Розділ II
Заповнюють далі графу 12, в якій обчислюються наближені абсциси X'. Абсциса X' початкової точки Х^8 = 0. Абсциса наступної точки Х'9% дорівнює довжині лінії S38_98 = 423,678 м, округленій до цілих метрів: +424. Для точки № 99 
і так далі. Для кінцевої точки № 40
Х'40 = +2060. Далі знаходять абсцису центра ваги ходу Хц:
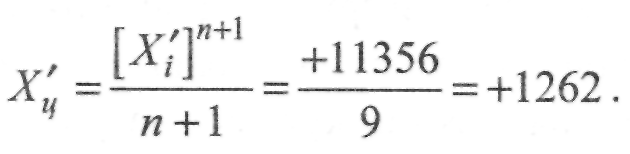
У графі 13 обчислюють абсциси точок ходу відносно центра ваги:
У графі 14 обчислюють квадрати цих абсцис 
та їхню суму 
Далі у допоміжній графі 15 обчислюють:
1. Поздовжній і поперечний зсуви t і и. Необхідні формули виписані у цій графі.
2. Поправки в лінії. Робоча формула: 
(є визначається з точністю до сьомого знака після коми). Поправки у лінії у міліметрах записані у графі 4 над виміряними лініями.
Для отримання зрівноважених довжин S поправки алгебраїчно
додаються до виміряних ліній. Зрівноважені лінії подано у графі 5.
|
3. Поправки в кути. Робоча формула: 
, де(й* = р"
[У] ■
Значення со" також обчислюється з точністю до сьомого знака після коми. Поправки V* записані під виміряними кутами у графі 2. Контроль поправок у кути: [v*] = 0. Кути округляються до 1".
4. Поправки в дирекційні кути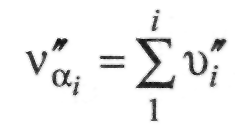 
. Ці поправки записані над
приблизними дирекційними кутами у графі 3.
Щоб знайти зрівноважені дирекційні кути, ці поправки алгебраїчно додають до наближених значень дирекційних кутів. Зрівноважені дирекційні кути у відомості не записані. За бажанням їх можна записати в графу 3 під наближеними дирекційними кутами, взявши їх у дужки. Обчислення закінчуються заповненням граф 8 і 9 та 10 і 11. У графах 8 і 9 записуються ув'язані прирости координат, обчислені за зрівноваженими дирекційними кутами та довжинами ліній S1.
Планові геодезичні мережі
Головним контролем правильності виконаного зрівноваження є рівності
Інакше кажучи, оскільки прирости координат зрівноважені, то їхні суми повинні дорівнювати різницям координат кінцевої та початкової заданих точок (не повинно бути нев'язок).
У графах 10 і 11 обчислюють кінцеві (точні) координати пунктів 
Оцінка точності кутів та ліній за результатами зрівноважень може бути виконана на основі знайдених поправок.
Таблиця II.8.S
