Оптично-віддалемірна полігонометрія

11.7.1. Принцип роботи та класифікація оптичних віддалемірів

Вимірювання довжин оптичними віддалемірами ґрунтується на роз­в'язанні дуже витягнутого, так званого паралактичного трикутника за кутом (р та базисом Ь (рис. И.7.1), перпендикулярним до лінії. Із трикутника АВМ маємо:

b
_{s =} ^_. (И.7.1)

Ф

Оскільки кут ф малий, то

Планові геодезичні мережі

 

Рис. II. 7.1. Паралактичний трикутник AMN для визначення довжини AB=S

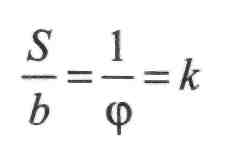
Тому

У цій формулі кут ф у радіанах. Відношення

(П.7.2) коефіцієнт

віддалеміра. Оскільки ф = — і р' = 3438', то для ф' = 34,38' (кутових мінут),

Р k =100. Отже,

(П.7.3)

Оптичні віддалеміри, залежно від положення базису b, поділяються на:

1) віддалеміри з базисом, відокремленим від кутомірного приладу;

2) віддалеміри з базисами, поєднаними з кутомірним приладом (відда­леміри внутрішньобазисні).

Останні віддалеміри використовуються для вимірювання віддалей до недоступних та важкодоступних предметів.

За способом визначення елементів паралактичного трикутника оптичні віддалеміри можна класифікувати так:

• віддалеміри одинарного зображення;

• віддалеміри подвійного зображення. Конструктивно оптичні віддалеміри поділяються на:

 

1) віддалеміри з постійним (відомим) базисом b та змінним кутом ф, що вимірюється;

2) віддалеміри зі змінним базисом Ь, що вимірюється та постійним (відомим) кутом ф.

Розділ II

Відцалеміри одноразового зображення з постійним кутом ф та змінним базисом Ь - це вже відомі з першого курсу ниткові відцалеміри. Відносні похибки вимірювання ліній нитковими віддалемірами наближено дорівнюють 1/300-1/400. Така точність недостатня для полігонометрії навіть 2 розряду.

Вищу точність мають віддалеміри одноразового зображення з постійним базисом Ь та точно виміряним змінним кутом ф, а також віддалеміри подвійного зображення, які і будуть розглянуті далі.

11.7.2. Віддалемір із постійним базисом та змінним кутом

У комплект такого віддалеміра входить точний або високоточний оптич­ний теодоліт та горизонтальна рейка (базис), яка встановлюється на штативі. Рейка без поділок, з марками на кінцях. Довжина рейки 2-3 м.

Для такого віддалеміра справедлива формула (П.7.2). Розрахуємо його точність. Для цього спочатку прологарифмуємо (П.7.2):

(П.7.4)

In S = In b - In ф. Тепер, диференціюючи (ІІ.7.4) за обома параметрами, матимемо:

(ІІ.7.5)

 

Рис. II. 7.2. До пояснення принципу роботи віддалеміра з постійним базисом Перейдемо від диференціалів до середніх квадратичних похибок:

(П.7.6)

S [ь) ф

Планові геодезичні мережі

Довжина базису b може бути визначена як завгодно точно, якщо прийняти т_ь = 0. На підставі (ІІ.7.6) матимемо:

Визначимо ф з (П.7.2):

Підставляючи у (ІІ.7.7) значення ф з (ІІ.7.8), отримаємо:

(ІІ.7.7)

(П.7.8)

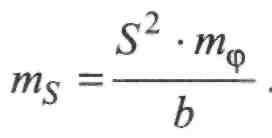
(П.7.9)

Переходячи від т_ф у радіанній мірі до кутової міри /я* (у секундах) остаточно маємо:

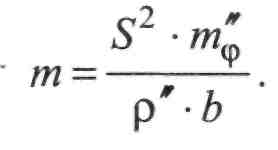
(П.7.10)

Як бачимо, похибка такого віддалеміра прямо пропорційна до квадрата вимірюваної довжини та похибки вимірювання кута т" і обернено пропорційна

до довжини базису Ь. Це означає, що для підвищення точності роботи від­далеміра необхідно:

1) вимірювати кут ф з мінімально можливою похибкою;

2) застосовувати якомога довші базиси Ь;

3) основне: виконувати вимірювання ліній короткими відрізками, встановлюючи віддалемір та рейку у створі лінії, яка підлягає визначенню (див. рис. П.7.3).

Рис. 11.7.3. Принцип створної короткобазисної полігонометрії

Такий метод вимірювання ліній називають методом створної короткоба­зисної полігонометрії.

Нехай таким віддалеміром вимірюється лінія завдовжки S = 200 м. Розрахуємо відносну похибку вимірювання цієї лінії, якщо довжина базису

Розділ II

b = 2 м, а похибка вимірювання куга т" = 1" (це практично мінімальна

похибка вимірювання кутів точним теодолітом). Запишемо формулу (П.7.10 у вигляді:

(II. 7.11)

Розрахунки дають:

Щ_

S

Як бачимо, такими відрізками (по 200 м) можна виконувати вимірювання ліній у теодолітному ході, а не в полігонометрії. У полігонометрії найнижчої точності (2 розряд) допустима відносна похибка, як відомо, дорівнює

(II. 7.12)

Розрахуємо допустиму довжину відрізка, якщо точність його вимірювання повинна становити 1/5000. На підставі (П.7.11)та (П.7.12) запишемо:

1 S-m^

5000 р'-Ь Розв'язуючи (П.7.13) відносно S, маємо:

(ІІ.7.13)

(П.7.14) Для тих самих значень Ь і от_ф отримуємо:

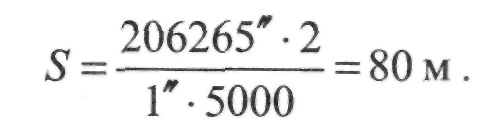
Якщо кути 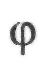будуть вимірюватися з абсолютною похибкою 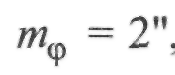, що

ймовірніше, тоді, відповідно:

5= 40 м. Отже, можливості використання в полігонометрії віддалеміра однора­зового зображення з постійним базисом доволі обмежені. Але, все-таки, точність такого віддалеміра майже на порядок вища, ніж ниткового віддалеміра, і ним можна прокладати полігонометрію 2 розряду.

11.7.3. Віддалеміри подвійного зображення

Оптичні віддалеміри подвійного зображення поширеніші у виробництві, ніж віддалеміри одноразового зображення. У таких віддалемірах, створених у кінці XIX століття, промені світла, що йдуть через об'єктив зорової труби,

Планові геодезичні мережі

розділяються на два пучки. Це досягається завдяки тому, що перед об'єктивом ставлять оптичний клин, який перекриває половину поля зору труби (рис. И.7.4).

Рис. 11.7.4. Оптичний клин: а - загальний вигляд; б - оптичний клин перекриває половину об'єктива зорової труби

Вертикальний розріз зорової труби з оптичним клином, встановленим на об'єктив, показано на рис. ІІ.7.5.

Горизонтальна вісь обертання труби проходить через точку О. Точка Р -так звана аналатична (вимірювальна) точка. Якраз у цій точці відбувається розділення (заломлення тієї частини променів світла, що проходить через об'єктив і клин). Та частина променів, яка проходить тільки через об'єктив, не заломлюється. У результаті в полі зору труби видно дві рейки, зміщені по вертикалі одна відносно одної, тобто видно подвійне зображення рейки. Інакше кажучи, точка Р проектується на рейку подвійно: у точці М тав точці./V.

Рис. II. 7 '.5. Вертикальний розріз зорової труби з оптичним клином та принцип роботи

віддалеміра подвійного зображення: 1 - окуляр; 2 - фокусувальна лінза;

З - об'єктив; 4 - оптичний клин

Якщо на рейці між точками М та N є п поділок рейки, а одна поділка завширшки a, тоді відрізок MN = an.

Розглядаючи трикутник PMN, запишемо:

(П.7.15)

Розділ II

або

(ІІ.7.16)

Оскільки кут ф незмінний, то й ctg ф - стала величина. Позначимо ^ф =С'. Тоді (II.7.16) набуде вигляду:

(П.7.17) Введемо нове позначення:

(П.7.18) отримаємо:

(П.7.19)

Формула (П.7.19) така сама, як і формула ниткового віддалеміра. Проте завдяки подвійному зображенню відрізок на рейці п ■ а може бути виміряний значно точніше ніж нитковим віддалеміром. У цьому перевага віддалеміра подвійного зображення порівняно з нитковим віддалеміром. Завдяки саме цій перевазі віддалеміри подвійного зображення значно точніші від віддалемірів одноразового зображення.

Розглянутий тільки що віддалемір подвійного зображення з постійним кутом ф та змінним базисом Ь = ап. Інколи замість оптичного клина перед

об'єктивом труби розташовують лінзові компенсатори, які дають змогу не тільки змінювати, але й вимірювати змінний кут ф між двома пучками про­менів. Тоді ми маємо віддалемір з постійним базисом b (горизонтальним або вертикальним) та змінним кутом ф.

Оптичні віддалеміри, як правило, є віддалемірами подвійного зображення.

Відповідно до ДЕСТу в СРСР випускали оптичні віддалеміри трьох типів. Всі вони подвійного зображення.

ДН8 (віддалемірна насадка, 8 см - похибка на 100 м довжини). За допомогою ДН8 вимірюються нахилені (не редуковані на горизонтальну площину) віддалі. Це віддалемір з постійним базисом Ь та змінним кутом ф. Рейка встановлюється на штативі горизонтально. Можна вимірювати довжини від 50 до 700 м з відносною похибкою 1:1000. Використовується для вимірю­вання ліній у теодолітних ходах. Може бути застосована в полігонометрії, якщо виконувати вимірювання ліній створним методом короткими відрізками.

ДНР5 (віддалемірна насадка, редукційна, 5 см - похибка на 100 м довжини). Дає змогу (для кутів нахилу до 12°) автоматично редукувати й одержувати горизонтальні прокладення ліній з відносною похибкою 1:1000-1:2000 завдовжки 20-120 м. Рейка двостороння, вертикальна. Це віддалемір з постійним кутом ф та змінним базисом Ь. Використовується так само, як і ДН8.

Планові геодезичні мережі

Д-2 (відцалемір, 2 см - похибка на 100 м довжини). Це удосконалений віддалемір ДН8; також з постійним базисом Ь та змінним кутом ф. Рейку можна встановлювати на штативі горизонтально або вертикально. Дає змогу вимірювати похилі (не редуковані) віддалі 40-400 м з відносною похибкою 1:5000. Можна вимірювати віддалі до 700 м, тільки тоді точність 1:1000. Використовується для вимірювання ліній у полігонометрії 2 розряду та в теодо­літних ходах.

11.7.4. Суть паралактичної полігонометрії

Траверсна полігонометрія з вимірюванням ліній підвісними мірними приладами потребує значних затрат праці. Тому, коли ще не було світло-віддалемірів, пошуки нових, посередніх методів вимірювання ліній були дуже актуальною науковою проблемою.

Як відомо, оптимальна довжина ліній полігонометрії 4 класу 500 м, а максимальна - 3 км. Враховуючи, що допустима довжина ходу 14 км, то для довжини ліній 1000 метрів у ході буде 14 сторін. Розрахуємо необхідну точність вимірювання ліній ходу з такими сторонами. Скористаємося відомою розра­хунковою формулою для висячого ходу:

\2»2

(Н.7.20)

У правій частині (ІІ.7.20) перший та другий члени є складовими відносної похибки — висячого ходу, викликаними відповідно похибками вимірювання ліній та кутів. За умови рівності цих двох членів можна записати:

або

М_v2(Щ

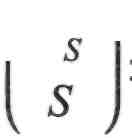
(т ^ Розв'яжемо (П.7.21)відносно ——

(П.7.21)

(ІІ.7.22)

Розділ II

Оскільки для 4 класу полігонометрії

= 14

то для п

отримаємо:

S 10000

Жодний оптичний віддалемір не дає такої точності для S = 1000 м. У

1836 р. проблема швидкого визначення була успішно вирішена В.Я. Струве,

який запропонував паралактичну ланку полігонометрії. Головна відмінність

відомої вже полігонометричної ланки з коротким базисом (з горизонтальною

рейкою, завдовжки 2-3 м) і паралактичною ланкою в тому, що в цій ланці

застосовують значно довший базис, виміряний мірними дротами. Така ланка

показана на рис. ІІ.7.6.

Рис. 11.7.6. Панка паралактичної полігонометрії Розрахуємо спочатку необхідну величину паралактичного кута. Оскільки

(ІІ.7.23)

якщо т" =2", можна записати:

(П.7.24)

10000 ф*

А тому ф*= 20000", або ф°= 5,6°. Залишається знайти необхідну довжину базису Ь. Відповідно до (ІІ.7.2):

або

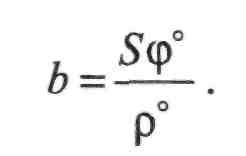
(П.7.25)

Планові геодезичні мережі

Тоді для S ■ 1000 м, матимемо:

Отже, для довжини мірного дроту 1₀ = 24 м достатньо буде відкласти чотири мірні дроти. Під час вимірювання ліній завдовжки 1000 м у траверсній полігонометрії необхідно буде відкласти у створі більше ніж 40 дротів. Звідси зрозуміло, як істотно зменшаться затрати часу, якщо використовувати паралактичні ланки навіть при тому, що ще потрібно в кожній ланці точно вимірювати кути.

Як очевидно з розрахунків, точність полігонометричної ланки В.Я. Струве залежить від величини кутаф. Проте для збільшення кута ф необхідно збіль­шувати довжину базису. У зв'язку з цим професор А.Д. Моторний запропо­нував [17] ланку полігонометрії, у якій базис розташовано не перпендикулярно до лінії, а вздовж лінії, тобто базис є частиною лінії, що визначається. Для однакових довжин базисів, але довших перпендикулярів (які не вимірюються), така ланка дає змогу збільшити кути ф і отримати значно вищу точність

визначення S. Для однакових за довжиною базисів та величин кутів ф, навпаки, точність ланки Струве дещо вища.

11.7.5. Суть віддалемірно-базисної полігонометрії

Віддалемірно-базисна полігонометрія - це поєднання віддалемірних визначень базисів з паралактичними ланками. Такий метод дуже еластичний і може застосовуватись у найважчих топографічних умовах. Як видно з рис. ІІ.7.7, базис Ь може бути виміряний мірним дротом, якщо лінії ходу S_x, S₂, S₃ - довгі, більші за 1 км або частіше, методом короткобазисної полігонометрії (Ь= 2-3 м), якщо лінії 5, - короткі (50-100 м). Знайшовши з паралактичної ланки довжину BN = d, далі, розв'язуючи трикутники ANB, BNC, визначають довжини сторін ходу S_l, S₂ тощо.

Виникає питання про найвигідніше співвідношення між Ь, d та S. Тео­ретичними дослідженнями доведено, що найвигіднішими, тобто найточнішими будуть ланки, коли виконується рівність

(П.7.26)

При цьому повинні бути наближено однакові кути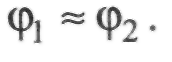

Розділ II

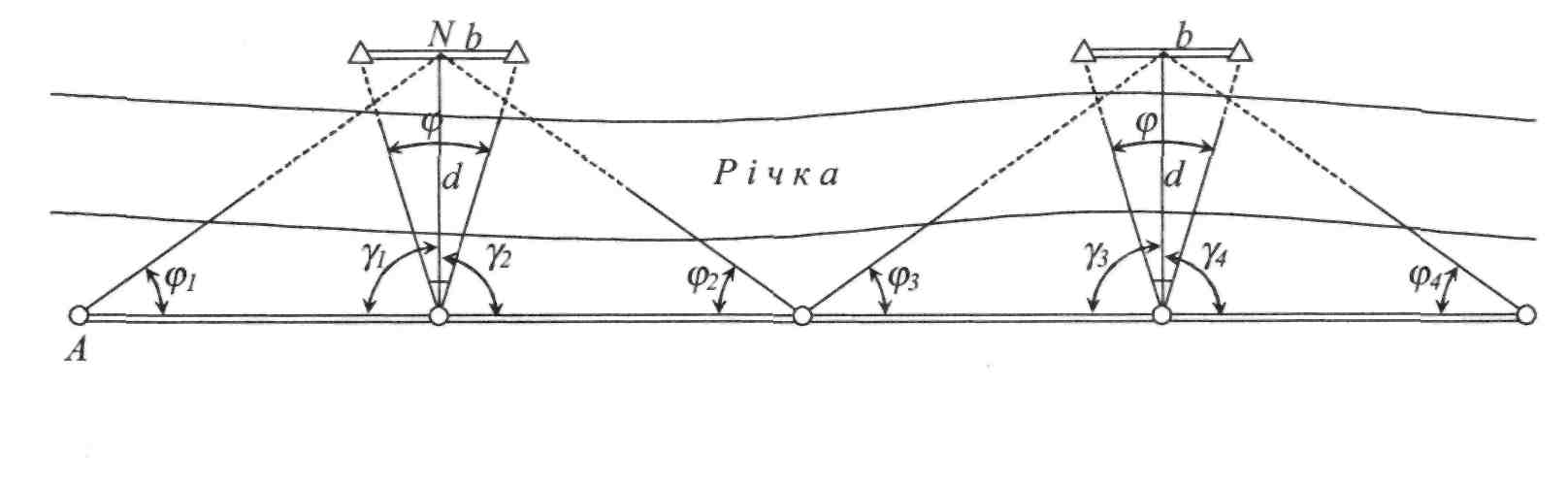
S/ В S2 C S? S4

Рис. 11.7.7. Ланка віддалемірно-базисноїполігонометрії

II. 7.6. Типи паралактичних і віддалемірно-базисних ланок

Паралактичні ланки поділяються на прості та складні. Подамо деякі типи ланок, що можуть бути застосовані у разі відсутності у виконавця робіт світловіддалемірів.

Планові геодезичні мережі

11.8. Строге зрівноваження полігонометричних ходів

11.8.1. Недоліки спрощених методів зрівноваження

Згадаємо, як ми виконували обчислення координат теодолітного ходу, прокладеного між точками з відомими координатами, а також відомими початковим і кінцевим дирекційними кутами.

Аналогічно можна виконувати обчислення координат полігонометричного ходу. У теодолітному ході ми спочатку знаходили кутову нев'язку за формулою

п+1 л+1 де £ Р і X Рш ~ відповідно практична і теоретична сума кутів ходу. Потім

(ІІ.8.1)

вводили поправки у виміряні кути. Сума поправок у кути Ida. \ повинна дорівнювати нев'язці з оберненим знаком:

(ІІ.8.2)

Це перша умова, яку має задовольняти виправлення кутів.

Потім за виправленими (зрівноваженими) кутами ми знаходили дирек-ційні кути сс_г, а, маючи ще і виміряні довжини 5,-, визначали прирости коор­динат

Ax_t = S_t ■ cos ос,; Ay_t = S, • sin ос,. (ІІ.8.3)

Розділ II

Далі окремо (незалежно від кутів) зрівноважували прирости координат. Спочатку знаходили нев'язки за відомими формулами

(II. 8.4)

(ІІ.8.5)

Нев'язки розподіляли в прирости координат, виконуючи ще дві умови: суми поправок у прирости абсцис та ординат [й?Лх₍] та [rfAy,] повинні дорів­нювати нев'язкам /_х і f з оберненим знаком:

(ІІ.8.6) (II. 8.7)

За виправленими (ув'язаними) приростами знаходили координати вершин ходу Х_і і Y_i. Здається, ніби три геометричні умови, що виникають у такому ході, виконані введенням поправок J(3_; в кути radAx_t, dAy_t - у прирости координат. Ось ці три умови, записані у вигляді рівнянь:

і п умова абсцис Хк = Хп + ]£ &х ',

умова дирекційних кутів а_к =ос„ + ХРл^в.-180(и + і);

(П.8.8)

умова ординат Y_K = Y„ + X &у_ув

І

У (II.8.8) прийняті позначення: - ліві (стосовно напрямку ходу),

ув'язані кути повороту; 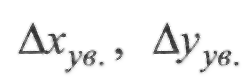- ув'язані прирости координат; а_п, а_к-

задані початковий і кінцевий дирекційні кути; 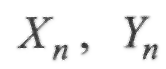- задані координати

початкової точки ходу; - координати кінцевої точки.

Але ці три умови (рівняння) розв'язувалися окремо.

Спочатку виконана умова , а потім, тільки після обчислення

приростів координат, виконано умови: 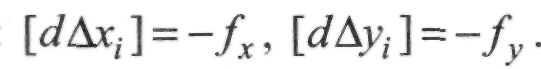Ці три геомет-

ричні умови взаємозалежні. Справді, зміна р\ кутів ходу викличе зміну довжин сторін ходу Sj. А це не враховано. Три рівняння потрібно розв'язувати разом. Тому, фактично, три геометричні умови, що виникають у ході, не задовольняються.

Планові геодезичні мережі

Щоб впевнитися в цьому, будемо за розрахованими нами координатами розв'язувати обернені геодезичні задачі, тобто знаходити довжини ліній S-, а також дирекційні кути а,', а потім кути повороту (3^. Тоді виявиться, що

, тобто ні ув'язані кути не будуть такими, як

виправлені поправками (d$_t) кути р,'; ні обчислені за координатами довжини ліній S'j не будуть такими, як виміряні S_t. Це означає, що знайдені координати не є такими, що задовольняють геометричні умови ходу, не є найімовірнішими.

У цьому і полягають недоліки спрощених методів зрівноваження. Вказані недоліки виникають через те, що ми не враховували залежностей між лініями та кутами. Потрібно поправки в кути та лінії шукати з одночасного розв'язання трьох геометричних умов, що виникають у ході.

Такі зрівноваження, коли знаходять поправки у кути та лінії з одночасного розв'язання умовних рівнянь, називаються строгими (точними). Накладається додаткова умова: сума квадратів поправок у кути та лінії повинна дорівнювати мінімуму [W] = шіп. До того ж обґрунтовано вибираються ваги вимірів кутів

та ліній.

Існують два методи строгого зрівноваження (вирівнювання) геодезичних ходів та мереж: корелатний та параметричний. Ці методи детально розгля­даються в теорії ймовірностей. Практичне застосування названих методів у геодезії, передусім у полігонометрії, буде висвітлено далі.

11.8.2. Кількість вимірів та невідомих у полігонометричному ході. Необхідні та надлишкові виміри

Нехай маємо полігонометричний хід, прокладений між "твердими" (відо­мими) пунктами, показаний на рис. П.8.1.

Рис. 11.8.1. Полігонометричний хід, прокладений між відомими пунктами та дирекційними кутами

У ході виміряно п ліній та (я +1) кутів. Кутів у ході завжди на один біль­ше ніж ліній, якщо виміряні також і кути (3j тар\,₊₁, що межують з лініями

Розділ II

тріангуляції. Отже, усього вимірів: (га + 1) + га = 2я + 1. Невідомими є координати пунктів ходу, показаних кружками. їх у ході завжди на одиницю менше ніж ліній. Невідомих абсцис Х_{ - (п -1). Невідомих ординат Y_t - (га -1). Усього невідомих (га - 1) + (и -1) = 2га - 2.

Знайдемо кількість надлишкових вимірів: {2га + і}-(2и-2) = 3. Отже, в

полігонометричному ході, який прокладений між відомими пунктами, завжди є три надлишкові виміри. Вони не є "непотрібними". Саме надлишкові виміри приводять до того, що в ході виникають геометричні умови, про які йшлося вище. Завжди в ході або мережі кількість умов дорівнює кількості надлишкових вимірів.

Знайдемо у наведеному ході "надлишкові" виміри, тобто такі виміри, які можна було б не робити, а всі невідомі координати пунктів знайти. Якщо обчислювати координати точок від початкової точки Т_поч, тоді знайдемо координати всіх точок, зокрема Х_п, Y_n точки Р_п без вимірів кутів (3„, Р_л+1 та лінії S_n. Якщо, навпаки, обчислювати координати точок від кінцевої точки Т_кін, тоді знайдемо координати всіх точок, зокрема Х₂, Y₂ точки Р₂ без вимірів кутів (3], Р₂ ^та ліній S.

Нарешті, можна частину точок обчислити від початку ходу, а частину -від кінця ходу. Тоді надлишковими будуть, наприклад, два кути й одна лінія, позначені на рис. II.. 1 хрестиками.

Надлишкові вимірювання спонукають до контролю вимірів і можливості зрівноваження ходів або мереж. За відсутності "надлишкових" вимірів хід перетворюється на "висячий" (спирається тільки на один відомий пункт), унеможливлюється контроль вимірів та зрівноваження ходів. Зрозуміло, що зникають і геометричні умови, що виникають у ході чи мережі.

Тому надлишкові виміри є дуже важливими.

11.8.3. Виведення формул, що зв'язують поздовжній та поперечний зсуви ходу з нев'язками по осях координат

На рис. ІІ.8.2 показано витягнутий полігонометричний хід, прокладений між відомими точками А та В.

Але координати усіх точок ходу, зокрема точки В, обчислювались не за зрівноваженими, а за виміряними лініями і кутами, починаючи від точки А. У результаті кінцева точка ходу зайняла положення В'. Отже, відрізок В'В = f_s -це лінійна нев'язка ходу. З'єднаємо точки А та В' прямою (замикаючою) і

Планові геодезичні мережі

дещо продовжимо її. Дирекційний кут замикаючої а. Дирекційний кут нев'язки є. Довжина замикаючої АВ' =L. Спроектуємо точку В на коорди­натні осі X та 7 і на замикаючу. Отримаємо точки В_х, В₂,В₃.

Рис. 11.8.2. До виведення залежності між зсувами t і и та нев'язками по осях координат f_x та f

Як видно з рисунка, відрізки: В'В_Х= ВВ₂ =f_x\ В'В_г = ВВ_Х -f_y- Ці відрізки дорівнюють нев'язкам /_х та f. Відрізок В'В₃ = t - поздовжній зсув; а ВВ_г = и- поперечний зсув. Проектуючи хід на осі X та Y, одержимо суми приростів координат [Аг] та [Ау].

(ІІ.8.9)

Безпосередньо з рисунка маємо:

(II. 8.10)

З рисунка також можемо записати:

Розділ II

Розкладаючи cos (є - а) та sin (є - а), отримаємо:

(II. 8.11) (П.8.12)

Враховуючи (II.8.10), маємо:

(ІІ.8.13)

(П.8.14)

Оскільки з цього самого рисунка

(ІІ.8.15)

(ІІ.8.16)

то

(ІІ.8.17)

(И.8.18)

(П.8.19)

Формули (II.8.17), (ІІ.8.18) пов'язують зсуви ходу t, u з нев'язками по осях координат f_x,f_y.

11.8.4. Виведення умовних рівнянь, що виникають у полігонометричному ході, прокладеному між відомими пунктами

Скористаємось розглянутими в п. II. 8.1 відомими вимогами рівності суми поправок у кути та у прирости координат відповідним нев'язкам, взятим з оберненим знаком.

Ці рівності запишемо так:

Планові геодезичні мережі

Припустимо, що ми нев'язку /о' порівну розподілили в усі виміряні кути.

Нехай виникла необхідність у виправлені кути ввести ще якісь вторинні поправки. Тоді сума цих поправок повинна дорівнювати нулеві. У про­тилежному випадку в ході з'явиться нова нев'язка. Але, якщо ми замінили виміряні кути Р; первинними поправками, то зміняться і дирекційні кути, а, отже, зміняться нев'язки f'_x та f' Одночасно виникне необхідність змінити

поправки у прирости абсцис і ординат.

У зв'язку з цим рівняння (ІІ.8.20) змінюються, і їх запишемо так:

Як відомо, прирости абсцис та ординат знаходять за формулами

(П.8.21)

Продиференціюємо ці формули:

(П.8.22)

 

(ІІ.8.23)

Значення dAx та dAy із рівнянь (ІІ.8.23) підставимо у початкові рівняння (П.8.21), враховуючи (П.8.22). Отримаємо:

(II. 8.24)

Перейдемо від поправок у дирекційні кути da_t до поправок у виміряні кути с/р,. Для цього скористаємося залежністю між дирекційними кутами та кутами повороту. Припустимо, вимірялись ліві по ходу кути. Тоді можемо записати:

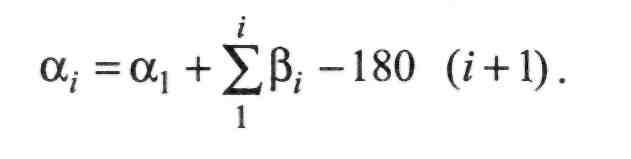
(ІІ.8.25)

Розділ II

Диференціюючи формулу (ІІ.8.25) за змінними кутами, одержимо:

1 Підставимо значення da_t з (ІІ.8.26) у (ІІ.8.24). Отримаємо:

(ІІ.8.26)

 

Позначимо

Запишемо суму А у розгорнутому вигляді:

(II. 8.27)

(ІІ.8.28)

Замінимо суми приростів ординат різницями координат відповідних

точок:

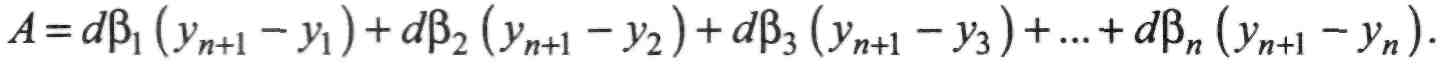
В останній сумі відсутній кут р„₊₁ і поправка ар„_н. Введемо цю поп­равку, скориставшись виразом, що дорівнює нулеві: d$_n+l (у_п+\ - у„₊\) ■ Цей ви­раз додамо до А. Тоді останній вираз можемо записати скорочено:

(ІІ.8.29) Введемо в рівняння (П.8.29) ординату центра ваги ходу:

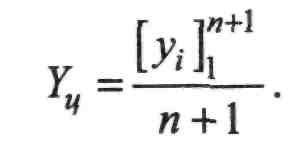
(ІІ.8.30)

Планові геодезичні мережі

Це можна зробити, враховуючи, що [с/р,] = 0. Отже, (П.8.29) можна за­писати так:

(ІІ.8.31) (П.8.32) (ІІ.8.33) (ІІ.8.34)

Позначивши в (II..31) різниці

де 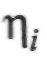- ординати точок ходу відносно центра ваги ходу. Матимемо:

Позначивши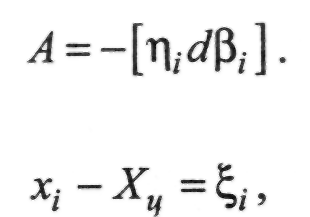

де - абсциси точок ходу відносно центра ваги, можемо за аналогією записати:

(П.8.35) Отже, умовні рівняння набувають вигляду:

(И.8.36)

Оскільки у рівняннях (П.8.36) поправки в кути с/р та в лінії dS записані двома літерами, доцільно ввести позначення: d$ = V; dS = CO, тобто позначити однією літерою поправки в кути V, а поправки в лінії со. Тоді записи (П.8.36) спростяться:

Це і є умовні рівняння в кінцевому вигляді.

(ІІ.8.37)

Розділ II

Зауважимо, що, як це буде очевидно з подальшого тексту, введення центральних координат спрощує обчислення під час зрівноваження ходу.

Необхідно, однак, для повнішого розуміння суті справи подати гео­метричну інтерпретацію координат центра ваги ходу Х_ц, У_ц та координат

точок ходу відносно центра ваги

 

Рис. 11.8.3. Геометрична інтерпретація координат центра вагиХ, Y та координат відносно центра ваги

Для простоти скористаємось витягнутим рівностороннім полігономет-ричним ходом із шести точок, п'яти сторін, показаного на рис. ІІ.8.3:

Планові геодезичні мережі

З рисунка, наприклад, очевидно, що в ході три ординати rjj, r\₂, Лз точок 1,2,3 від'ємні, а три гц, т\₅, Ц₆ точок 4, 5, 6 - додатні. До того ж зрозуміло, що сума [її, ] = 0. Аналогічно, сума [^ ] = 0.

11.8.5. Строге зрівноваження довільного полігонометричного ходу

корелатним методом

Розглянемо послідовність і суть методу. Нехай для довільного ходу маємо систему умовних рівнянь:

(ІІ.8.38)

Будемо одночасно розв'язувати ці рівняння під додатковою умовою:

де — ваги вимірювання ліній; 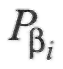— ваги вимірювання кутів.

Як відомо, ваги вимірювання - величини, обернено пропорційні до квадратів квадратичних похибок. Тому запишемо:

де - коефіцієнт випадкового впливу лінійних вимірів; щ- похибка

вимірювання кута; с - довільний коефіцієнт пропорційності.

Користуючись довільністю с, приймемо: с =\і. Тоді отримаємо:

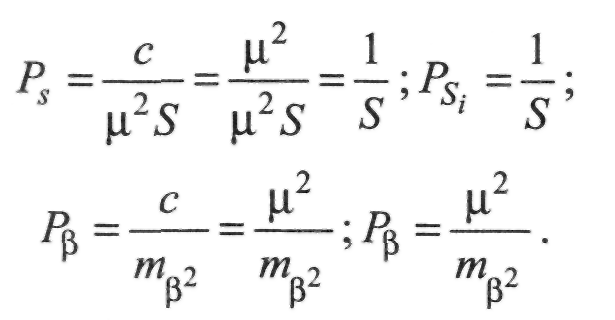
Отже, ваги виміру ліній - змінні величини й обернено пропорційні до довжини ліній, а кути мають однакові ваги, оскільки вимірюються приладами однієї точності і за однаковою програмою вимірювань.

Розділ II

Як відомо зі способу найменших квадратів, розв'язання (ІІ.8.37) під додатковою умовою (II.8.38) приводить до нормальних рівнянь корелат, яких буде стільки, скільки умовних рівнянь. У загальному вигляді нормальні рів­няння корелат записуються так:

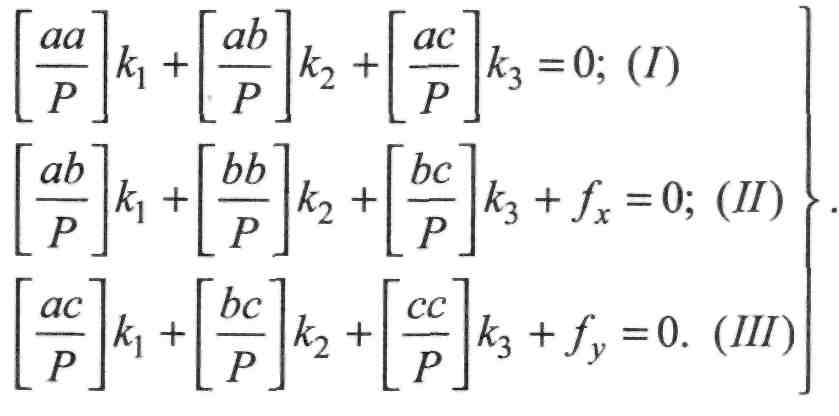
(ІІ.8.39)

У цих рівняннях к_х, к₂, к₃ - корелати - проміжні невідомі, знайшовши які, надалі можна буде обчислити шукані поправки у кути V, і в ліній ю₍.

Літерами a_t, Ь_і, с_і позначено коефіцієнти при невідомих поправках у кути та лінії відповідно в умовних рівняннях І, II, Ш системи (ІІ.8.37).

Складемо таблицю коефіцієнтів відповідно до (И.8.37) окремо для поправок у кути та в лінії.

Таблиця II. 8.1