Линейные операции над векторами и проекция вектора на ось

Сумма двух векторов

 

К линейным операциям над векторами относятся: сложение, вычитание векторов и умножение вектора на число.

Определение 8.2. Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , если вектор отложен из конца вектора (рисунок 8.3). Обозначается: = + .

Рисунок 8.3

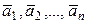Суммой векторов называется вектор, начало которого совпадает с началом вектора 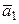, а конец – с концом вектора 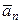, если каждый последующий вектор 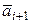отложен из конца предыдущего 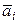для 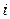= 1, 2, …, n – 1.

Свойства суммы векторов:

Рисунок 8.4

1. Свойство коммутативности: + = + (рисунок 8.4).

 

2. Свойство ассоциативности: ( + ) + = + ( + ) (рисунок 8.5).

 

Рисунок 8.5

 

3. + = .

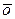4. + (− ) = .

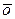Определение 8.3. Разностью двух векторов и (обозначается: − ) называется такой вектор , который в сумме с вектором даёт вектор , т. е. = − , если + = (рисунок 8.6).

Нетрудно заметить, что = − = + (− ).

 

Рисунок 8.6

 

Произведение вектора на число

Определение 8.4. Произведение вектора ≠ 0 на число α ≠ 0 называется вектор (обозначается = α), удовлетворяющий следующим условиям:

а) ;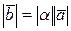

б) векторы и коллинеарны;

в) векторы и одинаково направлены при α > 0 и противоположно направлены при α < 0.

Свойства произведения вектора на число.

1) .

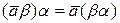2) .

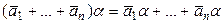3) .

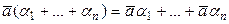4) Два вектора и коллинеарны тогда и только тогда, когда = α для некоторого α.

 

Проекция вектора на ось

Пусть в пространстве задана ось ℓ и некоторый вектор 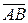(рисунок 8.7). Пусть А ₁ – проекция точки А на ось ℓ, В ₁ – проекция точки В на ось ℓ.

Рисунок 8.7

Проекцией вектора 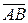на ось ℓ называется величина А ₁ В ₁ вектора 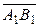, взятая со знаком «+», если 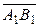совпадает с направлением оси ℓ, и со знаком «−», если 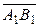противоположно направлен направлению оси ℓ. Обозначается: пр _ℓ .

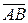Свойства проекции векторов на ось.

1. пр _ℓ 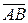= 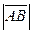× cos( 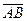^ ℓ) (рисунок 8.8);

2. пр _ℓ ( + ) = пр _ℓ + пр _ℓ (рисунок 8.9);

3. пр _ℓ (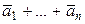) = пр _ℓ 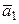+ … + пр _ℓ ;

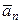4. пр _ℓ (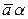) = (пр _ℓ ) 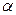(рисунок 8.10);

5. пр _ℓ (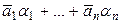) = (пр _ℓ 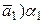+ … + (пр _ℓ ) .

	Рисунок 8.8		Рисунок 8.9

Рисунок 8.10

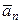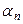Координаты вектора

 

Пусть в пространстве заданы прямоугольная система координат Oxyz и произв­ольный вектор 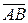. Пусть Х = пр _х 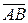, У = пр _y 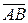, Z = пр _z 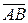. Проекции X, Y, Z вектора 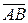на оси координат называют его координатами. При этом пишут 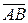= (Х, У, Z).

Теорема 8.1. Для любых точек А (х ₁; у ₁; z ₁) и В (х ₂; у ₂; z ₂) координаты вектора 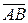, определяются формулами:

Х = х ₂ – х ₁, У = у ₂ – у ₁, Z = z ₂ – z ₁.

Доказательство. По определению Х = пр _х 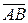. Если вектор 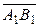направлен одинаково с осью Ох (рисунок 8.11), то пр _х 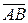= │ │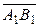= = 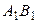х ₂ – х ₁, т. к. точке А ₁ соответствует координата х ₁, а точка В – координата х ₂.

Если вектор 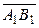направлен противоположно с осью Ох (рисунок 8.12), то пр_х 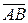= −│ │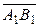= − = −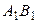(х ₁ – х ₂) = х ₂ – х ₁.

 

	Рисунок 8.11		Рисунок 8.12

Таким образом, для любых точек А (х ₁; у ₁; z ₁) и В (х ₂; у ₂; z₂) координата Х вектора 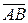вычисляется по формуле Х = х ₂ – х ₁.

Аналогично доказываются остальные формулы.

Пусть 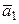= (х ₁; у ₁; z ₁), 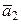= (х ₂; у ₂; z ₂),…, 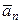= (х_n; у_n; z_n) – векторы пространства, 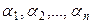– ненулевые числа. Используя свойства проекции векторов на ось, получим следующие утверждения:

1) = ( );

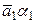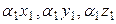2) 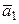+ + 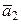… + 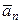= (х ₁+…+ х_n; y ₁+…+ у_n; z ₁+…+ z_n);

3) 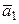− 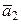= (х ₁ – х ₂; у ₁ – у ₂; z ₁ – z ₂);

4) +... + = ( );

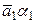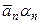5) 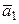= 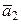Þ х ₁ = х₂, у ₁ = у ₂, z ₁ = z ₂.