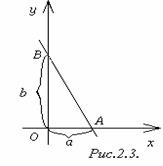
Пусть прямая пересекает оси Ox и Oy соответственно в точках A и B (рисунок 2.3). Пусть A (a, 0) и B (0, b). Из уравнения (2.5) имеем
= 
, 
+ 
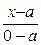= 1.
|
Уравнение + = 1 (2.6)
называется уравнением прямой в отрезках на осях координат.
Заметим, что прямые, параллельные координатным осям, и прямые, проходящие через начало координат, не могут быть записаны уравнением этого вида.
|
Рассмотрим на плоскости две прямые R1: y = k 1 x + b 1 и R2: y = k 2 x + b 2 с углами наклона к оси Ox соответственно φ1 и φ2 (рисунок 2.4).
Определение 2.2. Углом между прямыми R1 и R2 будем называть меньший из смежных углов, образованных этими пересекающимися прямыми.
На рисунке 2.4 таким является угол φ. Очевидно, что 0 ≤ φ ≤ 
. Из геометрических соображений устанавливаем зависимость между углами φ1, φ2 и φ: φ = φ2 – φ1. Возможны два случая:
1) угол φ =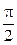 
, т. е. прямые R1 и R2 перпендикулярны;
2) 0 ≤ φ < 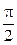. Тогда tg φ = tg (φ2 – φ1) = 
= 
.
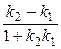Формула tg φ = 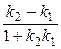, где 
(2.7)
позволяет вычислить угол между не перпендикулярными прямыми.
Условия параллельности и перпендикулярности прямых па плоскости
1) Если прямые R1 и R2 параллельны, то φ = 0. Тогда tg φ = 0 и из формулы (2.7) имеем k 2 – k 1 = 0 или k 2 = k 1. Таким образом, условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.
2) Если прямые R1 и R2 перпендикулярны, то φ = 
. Так как φ = φ2 – φ1 , то
φ2 =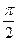 
+ φ1 и tg φ2 = tg(
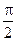+ φ1) = ctg φ1 = – 
, т. е.
k 2 = – 
. (2.8)
Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.
Вопросы для самоконтроля
1. Что называется уравнением линии на плоскости хОу?
2. Какой вид имеет уравнение прямой с угловым коэффициентом?
3. Какой знак имеет угловой коэффициент прямой, образующей с положительным направлением оси Ох острый угол? тупой угол?
4. Какой вид имеет уравнение прямой в отрезках наосях?
5. Напишите уравнение прямой в общем виде. Как найти угловой коэффициент этой прямой?
6. Как расположена в плоскости хОу прямая, уравнение которой Ах + Ву = 0; Ах + С = 0; Ах = 0; Ву = 0 (коэффициенты А, В, С отличны от нуля)?
7. Как найти точку пересечения двух прямых?
8. Как убедиться в том, что данная точка принадлежит данной прямой?
9. Как построить прямую, заданную соответствующим уравнением?
10. Какой вид имеет уравнение прямой, проходящей через данную точку и имеющей соответствующий угловой коэффициент?
11. Какой вид имеет уравнение прямой, проходящей через две данные точки?
12. Напишите формулу для определения угла между двумя прямыми на плоскости.
13. Сформулируйте условия параллельности и перпендикулярности двух прямых.
Взаимное расположение двух прямых на плоскости
