Линейные дифференциальные уравнения с постоянными коэффициентами удобно записывать в символической операторной форме
 , (3-10)
, (3-10)
где символ 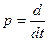 назван оператором дифференцирования,
назван оператором дифференцирования,
n-ая производная от  будет
будет 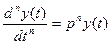 .
.
Дифференциальные уравнения высокого порядка, имеющие производные в левой и правой части, в операторной форме примет вид
 , (3-11)
, (3-11)
где  ,
,
 .
.
Многочлен  называют собственным оператором объекта (элемента), а многочлен
называют собственным оператором объекта (элемента), а многочлен  -входным оператором. Собственный оператор
-входным оператором. Собственный оператор  характеризует собственное движение описываемого объекта (элемента), то есть движения при отсутствии внешних воздействий. Входной опрератор
характеризует собственное движение описываемого объекта (элемента), то есть движения при отсутствии внешних воздействий. Входной опрератор  характеризует воздействие, приложенное к объекту (элементу). Отношение входного оператора
характеризует воздействие, приложенное к объекту (элементу). Отношение входного оператора  к собственному оператору
к собственному оператору  называют передаточной функцией
называют передаточной функцией  объекта (элемента АСР), описываемого линейным дифференциальным уравнением с постоянными коэффициентами.
объекта (элемента АСР), описываемого линейным дифференциальным уравнением с постоянными коэффициентами.
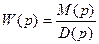 ,
,
тогда решение уравнения (3-11) может быть найдено в виде алгебраического уравнения

 (3-12)
(3-12)
Идею перехода к алгебраическому методу решения дифференциальных уравнений дал английский физик Хэвисайд, который и ввел символ 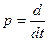 .
.
Однако при решении ряда задач с не нулевыми начальными условиями использование оператора дифференцирования 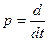 не давали адекватного ответа.
не давали адекватного ответа.
Строгое математическое обоснование такого перехода дал Пьер Симон Лаплас и этот метод получил название операционного исчисления или метод преобразований Лапласа, согласно которому решение дифференциальных уравнений переводится из плоскости оригиналов (плоскости действий переменной t) в плоскость изображений (переменной S). Выполняя действия над изображением оригинала получают изображение ответа. А затем по изображению ответа ищут его оригинал.
Допустим имеем функцию  , предположим, что эта функция удовлетворяет условиям Дерихле, существо которых:
, предположим, что эта функция удовлетворяет условиям Дерихле, существо которых:
а) непрерывность функции и ее производных, это значит в исследуемом интервале функция не имеет разрыва,
б) функция абсолютно интегрируема, т.е. интеграл функции от 0 до ∞ есть конечное число

Возьмем интеграл от функции 
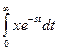 , где
, где 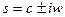 комплексная переменная,
комплексная переменная,
тогда интеграл уже не будет функцией от 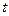 , но станет функцией от S.
, но станет функцией от S.
Обозначим 
Этот интеграл назван изображением функции по Лапласу, а то действие, которое отражает этот интеграл, называется прямое преобразование Лапласа. Принято записывать прямое преобразование по Лапласу как  , которое называют так же L-преобразованием.
, которое называют так же L-преобразованием.
Для большого количества функций изображения найдены.
Например, изображение постоянной величины:  .
.
 будет
будет  , если в действительной плоскости
, если в действительной плоскости 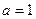 , то в плоскости изображений 1 становится величиной
, то в плоскости изображений 1 становится величиной  .
.
Изображение производной  :
:  ;
;  .
.
Американский математик Карсон предложил ввести преобразования вида  , то есть практически изменил масштаб величины. Законы, установленные Лапласом, остаются, но при этом
, то есть практически изменил масштаб величины. Законы, установленные Лапласом, остаются, но при этом  остается 1, а число
остается 1, а число  числом
числом  .
.
Запишем исходное уравнение
 (3-13)
(3-13)
в изображениях по Лапласу, умножив обе части уравнения на 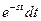 , получим
, получим
 (3-14)
(3-14)
Проинтегрируем уравнение (3-14) в области от 0 до ∞
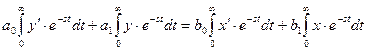 (3-15)
(3-15)
Пусть имеем нулевые начальные условия, то есть 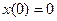 ;
;  , тогда в изображениях по Лапласу уравнение (3-15) примет вид
, тогда в изображениях по Лапласу уравнение (3-15) примет вид
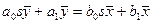 (3-16)
(3-16)
или 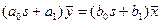 (3-17)
(3-17)
Последнее означает, что решение дифференциального уравнения в действительной плоскости –плоскости действительной переменной 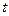 перевели в плоскость изображения- плоскость комплексной переменной
перевели в плоскость изображения- плоскость комплексной переменной 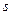 , и решают это уравнение как алгебраическое.
, и решают это уравнение как алгебраическое.
Далее по найденному изображению ответа находят его оригинал.
Для нахождения оригинала ответа надо воспользоваться обратным изображением Лапласа
 ,
,
для этого существует таблица функций обратных переходов.
Преобразуем дифференциальное уравнение, описывающее движение системы (3-11), по Лапласу, предположив нулевые начальные условия при его решении, введем обозначения:
 и
и  ,
,
где  и
и 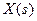 - изображения функции оригинала
- изображения функции оригинала  и
и 
получают
 , (3-18)
, (3-18)
здесь  ,
, 
При нулевых начальных условиях 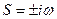 .
.
Используя обозначение  , решение уравнения (3-18) примет вид
, решение уравнения (3-18) примет вид 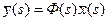
Это уравнение связывает изображения  выходной координаты системы с изображением
выходной координаты системы с изображением  -входного воздействия.
-входного воздействия.
Функция 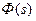 - характеризует динамические свойства системы и называется передаточной функцией
- характеризует динамические свойства системы и называется передаточной функцией 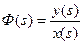 . Она представляет собой отношение изображения по Лапласу выходной координаты системы к изображению по Лапласу входного воздействия при нулевых начальных условиях. Подобное определение функции не находится в противоречии с ранее данным определением передаточной функции
. Она представляет собой отношение изображения по Лапласу выходной координаты системы к изображению по Лапласу входного воздействия при нулевых начальных условиях. Подобное определение функции не находится в противоречии с ранее данным определением передаточной функции  , т.к. для решения системы дифференциальных уравнений при нулевых начальных условиях комплексная переменная
, т.к. для решения системы дифференциальных уравнений при нулевых начальных условиях комплексная переменная 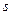 отождествлена с оператором дифференцирования
отождествлена с оператором дифференцирования  .
.
Таким образом, зная передаточную функцию системы 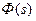 и определив изображение
и определив изображение  воздействия
воздействия  , приложенного к системе, можно найти изображение
, приложенного к системе, можно найти изображение  выходной координаты системы y(t), а затем, переходя от изображения y(s) к оригиналу
выходной координаты системы y(t), а затем, переходя от изображения y(s) к оригиналу  , получить процесс изменения выходной координаты при наличии входного воздействия.
, получить процесс изменения выходной координаты при наличии входного воздействия.
Имея передаточную функцию 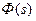 нетрудно определить амплитудно-фазовую характеристику этой системы, заменив
нетрудно определить амплитудно-фазовую характеристику этой системы, заменив  на
на 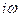
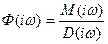 ,
,
где:  -частота нанесения входного воздействия и при установившемся колебательном движении системы – частота изменения ее выходной координаты.
-частота нанесения входного воздействия и при установившемся колебательном движении системы – частота изменения ее выходной координаты.






