АСР, как и любой ее элемент, называется линейной или нелинейной в зависимости от того линейной или нелинейной является ее математическая модель-система дифференциальных и алгебраических уравнений, связывающих между собой входные и выходные параметры системы. Все реальные системы являются в той или иной степени нелинейными системами. Нелинейность систем в большинстве случаев связана с нелинейностью реальных статических характеристик элементов АСР. Решение системы дифференциальных уравнений, описывающих поведение такой системы, в общем виде получить нельзя. Возникает необходимость линеаризовать, если это возможно, систему нелинейных уравнений математической модели, заменив ее более простой, приближенной линейной системой. Если уравнения модели АСР нелинейны из-за нелинейности статической характеристики ее элементов, то линеаризация уравнения сводится к замене нелинейной статической характеристики элемента  , (Рис.3.1,а,б) некоторой линейной функцией
, (Рис.3.1,а,б) некоторой линейной функцией  , где
, где  - выходной параметр,
- выходной параметр, 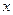 -входной параметр.
-входной параметр.
Математически эта замена производится путем разложения в ряд Тэйлора функции  в окрестности точки, соответствующей установившемуся состоянию. Геометрически это означает замену нелинейной статической характеристики
в окрестности точки, соответствующей установившемуся состоянию. Геометрически это означает замену нелинейной статической характеристики  касательной, проведенной к кривой в точке с координатами
касательной, проведенной к кривой в точке с координатами  ,
,  , соответствующей установившемуся состоянию работы объекта математического исследования.
, соответствующей установившемуся состоянию работы объекта математического исследования.
В других случаях линерализация производится путем проведения секущей, мало отклоняющейся от функции  в требуемом диапазоне изменения выходной величины объекта (Рис.3.1,в).
в требуемом диапазоне изменения выходной величины объекта (Рис.3.1,в).
 Рис. 3.1. Линеаризация статических характеристик.
Рис. 3.1. Линеаризация статических характеристик.
Нелинейные статические характеристики, линеаризуемые в требуемом диапазоне изменения выходной величины рассмотренными выше способами, называют несущественно нелинейными характеристиками. Наряду с ними имеются так же характеристики, которые не поддаются линеаризации. Последние называются существенно нелинейными (Рис. 3.2).

Рис. 3.2. Статические характеристики релейных элементов
а) идеального; б) с зоной нечувствтительности.
Аппроксимация такого рода разрывных характеристик прямой линией с постоянным углом наклона может привести к существенному искажению представлений о процессах, происходящих в реальной АСР.
Пусть поведение объекта исследования описывается нелинейным дифференциальным уравнением в общем виде:
 , (3.1)
, (3.1)
Установившееся состояние объекта характеризуется уравнением, для получения которого в уравнении (3-1)следует положить у=idem, x=idem.
 , (3.2)
, (3.2)
где  и
и  -значения координат, соответствующие установившемуся состоянию объекта, тогда координаты
-значения координат, соответствующие установившемуся состоянию объекта, тогда координаты 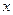 и
и  можно записать в виде
можно записать в виде
 ,
,
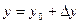 ,
,
где  и
и  -отклонения координат
-отклонения координат 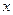 и
и  от установившегося состояния.
от установившегося состояния.
Уравнение (3-1) в отклонениях имеет вид  (3-3)
(3-3)
Разложим левую часть уравнения (3-3) в ряд Тейлора относительно точки установившегося состояния  .
.
 (3-4)
(3-4)
В левой части равенства (3-4) не записаны члены, содержащие отклонения  и
и  и их производные в степени выше первой. Частные производные в левой части уравнения (3-4) представляют собой некоторые числа, величины которых зависят от вида исходной функции
и их производные в степени выше первой. Частные производные в левой части уравнения (3-4) представляют собой некоторые числа, величины которых зависят от вида исходной функции  и значений координат
и значений координат  и
и  . Считая отклонения
. Считая отклонения  и
и  от установившегося состояния, а так же их производные по времени малыми и полагая, что функция
от установившегося состояния, а так же их производные по времени малыми и полагая, что функция  достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в уравнении (3-4) все члены, которые содержат отклонения
достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в уравнении (3-4) все члены, которые содержат отклонения  и
и  , а так же их производные выше первой,
, а так же их производные выше первой,
получим уравнение
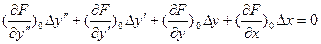 , (3-5)
, (3-5)
которое является линейным дифференциальным уравнением с постоянными коэффициентами  ,
,  ,
,  ,
,  .
.
Уравнение (3-5) представляет собой результат линеаризации уравнения (3-1).
Очевидно, что необходимым условием линеаризации уравнения является возможность разложения в ряд Тэйлора функции  в окрестности точки, соответствующей установившемуся состоянию. Линеаризованное уравнение (3-5) приближенно заменяет нелинейное уравнение (3-1) в некоторой малой окрестности точки с координатами
в окрестности точки, соответствующей установившемуся состоянию. Линеаризованное уравнение (3-5) приближенно заменяет нелинейное уравнение (3-1) в некоторой малой окрестности точки с координатами  . Как правило, с помощью уравнения (3-5) можно исследовать поведение объекта лишь при малых колебаниях входной и выходной координаты относительно установившегося состояния.
. Как правило, с помощью уравнения (3-5) можно исследовать поведение объекта лишь при малых колебаниях входной и выходной координаты относительно установившегося состояния.
Обычно при записи линеаризованного уравнения в левой его части оставляют лишь члены, содержащие отклонения выходной координаты, а все остальные члены переносят в правую часть. С учетом этого уравнение (3-5) можно переписать в виде:
 , (3-6)
, (3-6)
где 
Принято записывать уравнение не в приращениях, а в относительных величинах, относя приращения к неким базисным значениям параметров. Обозначим

За базисные могут быть теоретически выбраны любые значения параметра, обычно максимальные либо номинальные значения параметров, отвечающие выбранному установившемуся режиму, тогда уравнение (3-6) предстанет в виде
 (3-7)
(3-7)
обозначив  ;
;  ;
;  ;
;  ,
,
получим  , (3-8)
, (3-8)
где 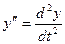 ;
;  ;
;
В итоге уравнение (3-8) будет иметь вид
 (3-9)
(3-9)
Совокупность такого вида уравнений описывает поведение динамической системы, решив которые можно получить описание переходного процесса в этой системе.
Постоянные коэффициенты уравнений могут быть определены либо аналитически, например, для тепловых объектов по данным теплового расчета объекта, его конструктивным характеристикам, либо из графиков статических характеристик. Последние строятся при постоянных значениях всех независимых переменных, кроме той, по которой вычисляется производная. Если статические характеристики линейны в широком диапазоне режимов работы или допустимо осреднение характеристик в широкой области, то полученные линейные уравнения применены для исследования так же при больших отклонениях  и
и  .
.






